Пространства непрерывных функций с дробным показателем гладкости. Часть 5, заключительная.
Начало.
Предыдущая часть.
В предыдущей части мы, внезапно, обнаружили и доказали, что пространства)
- несепарабельны.
Сегодня, как обещано, будет построен конкретный пример функции&space;\in&space;C^{0,1}[a,b])
, для которой погрешность кусочно-линейной аппроксимации не стремится к нулю при измельчении разбиения отрезка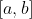
.
Напоминаю, норма пространства
задается выражением:
}&space;=&space;\begin{matrix}&space;\sup\\x\in[a,b]&space;\end{matrix}\left&space;|&space;f(x)&space;\right&space;|&space;+&space;\begin{matrix}&space;\sup\\&space;x_1,x_2\in[a,b],&space;\\&space;x_1&space;\neq&space;x2&space;\end{matrix}&space;\frac{\left&space;|&space;f(x_1)&space;-&space;f(x_2)&space;\right&space;|}{\left&space;|&space;x_1&space;-&space;x_2&space;\right&space;|})
Сестра, скальпель!
Для начала:
Упражнение (средней сложности): покажите, что если бы для любой функции&space;\in&space;C^{0,1}[a,b])
погрешность кусочно-линейной аппроксимации)
стремилась к нулю при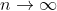
, то это означало бы сепарабельность
.
Теперь - к обещанному примеру.
Я уже упоминал, что исследование на сепарабельность пространств)
мне не удалось найти вообще нигде (разумеется, где-то оно таки есть, но где - я не знаю). Так что, нижеследующий пример вынут мною из головы. Если, вдруг (мало ли какие чудеса бывают), он в литературе не упоминается - вы все знаете на кого ссылаться, хехе. Ежели, напротив, кто-нибудь с ним уже сталкивался, подайте, пожалуйста на хлебушекссылочку.
Функцию построим в пространстве
.
Схема построения следующая: отрезок делим пополам, на левую часть ставим "колпачок" единичной высоты. Правую часть снова делим пополам, слева ставим "колпачок" высоты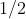
. Остаток делим пополам, на левую часть ставим "колпачок" высоты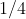
и т.д.
В результате, должна получиться вот такая картинка:

Очевидно, что
Единицу даст первое слагаемое нормы, двойку - второе, в сумме - тройка.
Давайте покажем, что для кусочно-линейной аппроксимации)
, построенной на равномерном разбиении отрезка на
частей:

Между прочим, этот предел может не существовать вообще.
Полное исследование указанного предела - дело достаточно громоздкое. Мы этим заниматься не будем. Вместо этого, я продемонстрирую вам, как ленивые математики применяют на практике принцип наименьшего действия.
Заметьте, для доказательства гнилой сущности нашей "колпачковой" функции, достаточно, чтобы было неверно следующее утверждение:
Предел существует и равен нулю.
Вот опровержением этого поклепа мы и займемся.
Итак, у нас есть некоторая числовая последовательность
. Как известно, если числовая последовательность сходится к некоторому пределу, то к тому же пределу сходится и любая ее подпоследовательность. В качестве такой "любой" подпоследовательности возьмем элементы с индексами
и поищем предел последовательности
.
Понятное дело, я такую подпоследовательность выбрал не случайно (хе-хе), а для того чтобы границы отрезков разбиения попадали в точки локальных максимумов и минимумов "колпачковой" функции.
В результате, кусочно линейная аппроксимация на разбиениях с индексами
будет выглядеть следующим образом:
При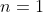
:

При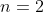
:

Соответственно, при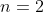
график функции&space;-&space;f_{2^{n+1}(x)}&space;\right&space;|)
имеет вид.

Здесь уже должно быть ясно, куда я клоню.
Очевидно (хотя рекомендую проверить), что:

Отсюда, вуаля, следует, что даже если предел
существует, то он равен двум, а вовсе не нулю. Бинго!
При этом, прошу заметить, что если бы мы рассматривали сходимость в пространстве
, то в пределе бы получился благополучный ноль. Увы, увы.
Таким образом, для "колпачковая" функции&space;\in&space;C^{0,1}[0,2])
погрешность кусочно-линейной аппроксимации не стремится к нулю с ростом
. Существование таких функций, конечно, прямо следовало из факта несепарабельности пространств)
. Но теория-теорией, а всегда интересно убедиться на практике.
На этом о пространствах)
- все.
В отдаленном светлом будущем, во время очередного припадкаприступа вдохновения, планирую рассказать немного о том, как эти пространства применяются в теории уравнений в частных производных, на примере теоремы Шаудера о разрешимости краевой задачи Дирихле для эллиптического уравнения второго порядка.
А вот и нет, в результате поговорилось о модулях непрерывности.
Продолжение.
Предыдущая часть.
В предыдущей части мы, внезапно, обнаружили и доказали, что пространства
- несепарабельны.
Сегодня, как обещано, будет построен конкретный пример функции
, для которой погрешность кусочно-линейной аппроксимации не стремится к нулю при измельчении разбиения отрезка
.
Напоминаю, норма пространства
задается выражением:
Сестра, скальпель!
Для начала:
Упражнение (средней сложности): покажите, что если бы для любой функции
погрешность кусочно-линейной аппроксимации
стремилась к нулю при
, то это означало бы сепарабельность
.
Теперь - к обещанному примеру.
Я уже упоминал, что исследование на сепарабельность пространств
мне не удалось найти вообще нигде (разумеется, где-то оно таки есть, но где - я не знаю). Так что, нижеследующий пример вынут мною из головы. Если, вдруг (мало ли какие чудеса бывают), он в литературе не упоминается - вы все знаете на кого ссылаться, хехе. Ежели, напротив, кто-нибудь с ним уже сталкивался, подайте, пожалуйста на хлебушекссылочку.
Функцию построим в пространстве
.
Схема построения следующая: отрезок делим пополам, на левую часть ставим "колпачок" единичной высоты. Правую часть снова делим пополам, слева ставим "колпачок" высоты
. Остаток делим пополам, на левую часть ставим "колпачок" высоты
и т.д.
В результате, должна получиться вот такая картинка:

Очевидно, что
Единицу даст первое слагаемое нормы, двойку - второе, в сумме - тройка.
Давайте покажем, что для кусочно-линейной аппроксимации
, построенной на равномерном разбиении отрезка на
частей:
Между прочим, этот предел может не существовать вообще.
Полное исследование указанного предела - дело достаточно громоздкое. Мы этим заниматься не будем. Вместо этого, я продемонстрирую вам, как ленивые математики применяют на практике принцип наименьшего действия.
Заметьте, для доказательства гнилой сущности нашей "колпачковой" функции, достаточно, чтобы было неверно следующее утверждение:
Предел существует и равен нулю.
Вот опровержением этого поклепа мы и займемся.
Итак, у нас есть некоторая числовая последовательность
. Как известно, если числовая последовательность сходится к некоторому пределу, то к тому же пределу сходится и любая ее подпоследовательность. В качестве такой "любой" подпоследовательности возьмем элементы с индексами
и поищем предел последовательности
.
Понятное дело, я такую подпоследовательность выбрал не случайно (хе-хе), а для того чтобы границы отрезков разбиения попадали в точки локальных максимумов и минимумов "колпачковой" функции.
В результате, кусочно линейная аппроксимация на разбиениях с индексами
будет выглядеть следующим образом:
При
:

При
:

Соответственно, при
график функции
имеет вид.

Здесь уже должно быть ясно, куда я клоню.
Очевидно (хотя рекомендую проверить), что:
Отсюда, вуаля, следует, что даже если предел
существует, то он равен двум, а вовсе не нулю. Бинго!
При этом, прошу заметить, что если бы мы рассматривали сходимость в пространстве
, то в пределе бы получился благополучный ноль. Увы, увы.
Таким образом, для "колпачковая" функции
погрешность кусочно-линейной аппроксимации не стремится к нулю с ростом
. Существование таких функций, конечно, прямо следовало из факта несепарабельности пространств
. Но теория-теорией, а всегда интересно убедиться на практике.
На этом о пространствах
- все.
В отдаленном светлом будущем, во время очередного припадкаприступа вдохновения, планирую рассказать немного о том, как эти пространства применяются в теории уравнений в частных производных, на примере теоремы Шаудера о разрешимости краевой задачи Дирихле для эллиптического уравнения второго порядка.
А вот и нет, в результате поговорилось о модулях непрерывности.
Продолжение.