Пространства непрерывных функций с дробным показателем гладкости. Часть 4.
Начало.
Предыдущая часть.
Рассматриваем пространство
, оно же
, с нормой:

Сегодня закрываем вопрос с сепарабельностью.
Погнали!
Ситуация с кусочно-линейной аппроксимацией кардинально меняется в случае, когда&space;\in&space;C^{0,1}[a,b])
.
Напомню, разбиение отрезка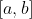
у нас равномерное, на
одинаковых частей.
Введем дополнительно:

Посмотрите на картинку, где я нарисовал тот самый ромбик из самой-самой первой части. Как вы, надеюсь, помните, из-за наложенного на функцию условия Липшица, функция)
, с зафиксированными на границах некоего отрезка (в нашем случае, элемента разбиения) значениями, не может покинуть границы небесно-голубого параллелограмма. Дабы не повторяться, я рекомендую тем, для кого этот факт непрозрачен, пройти сюда, где обсуждаются функции с условием Липшица.

Модули угловых коэффициентов прямых, образующих границы ромба, подчинены неравенству:

(Это непосредственно вытеркает из определения нормы
).
Отсюда, просто из элементарной геометрии, следует максимальная оценка погрешности кусочно-линейной аппроксимации в смысле нормы
:

Очень, кстати, удобная оценка, вполне применимая на практике. Еще лучше, если нам известна не только норма целиком, но и вклад второй компоненты (т.е. показатель Липшица). При использовании показателя Липшица вместо нормы данная оценка становится неулучшаемой.
Упражнение (чуть сложнее, чем простое): докажите оценку. Задачка на геометрию, практисски.
Однако, мы таки обсуждаем
, а вовсе не
.
Напомню:
}&space;=&space;\begin{matrix}&space;\sup\\x\in\Omega&space;\end{matrix}\left&space;|&space;f(x)&space;\right&space;|&space;+&space;\begin{matrix}&space;\sup\\&space;x_1,x_2\in\Omega,&space;\\&space;x_1&space;\neq&space;x2&space;\end{matrix}&space;\frac{\left&space;|&space;f(x_1)&space;-&space;f(x_2)&space;\right&space;|}{\left&space;|&space;x_1&space;-&space;x_2&space;\right&space;|})
Благодаря полученной выше оценке, имеем:
}&space;\leq&space;\left&space;\|&space;f&space;\right&space;\|_{C^{0,1}}\frac{b-a}{2n}&space;+&space;\begin{matrix}&space;\sup\\&space;x_1,x_2\in\Omega,&space;\\&space;x_1&space;\neq&space;x2&space;\end{matrix}&space;\frac{\left&space;|&space;f(x_1)&space;-&space;f(x_2)&space;-&space;(f_n(x_1)&space;-&space;f_n(x_2))&space;\right&space;|}{\left&space;|&space;x_1&space;-&space;x_2&space;\right&space;|})
Как видите, если для второго слагаемого справа можно было также, как для первого, указать подходящую оценку, или хотя бы показать его стремление к нулю при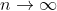
, то до окончательного доказательства сепарабельности
будет рукой подать.
Если бы... Если...
Короче, прекращаю тянуть резину за хвост в долгий ящик. Петух пропел трижды.
Пространство)
не обладает свойством сепарабельности.
Приплыли.
В тот момент, когда во время подготовки очередного поста, вместо ненапряжного доказательства сепарабельности в результате получилось вот ЭТО - шаблон у меня треснул с пушечным грохотом. Неожиданность, да.
Вообще, свойства пространств)
и сами они довольно скупо обсуждаются в литературе. А уж вопрос сепарабельности не упоминается вообще ни в одной из книжек, что у меня есть под рукой. Изначально, сепарабельность я хотел рассмотреть чисто для кучи, шоб було. Однако, в результате, это оказалась самой интересной частью работы. Шутка ли, нетривиальное несепарабельное пространство, более того, не искусственный какой случай, любимый лишь специалистами по функциональному анализу, а пространства, которые реально используются, например, в математической физике.
Лемма: если в некотором банаховом пространстве
существует несчетное множество
, такое, что попарные расстояния между его элементами больше некоторой фиксированной константы
, т.е. для любых
справедливо:

то пространство
- несепарабельно.
Упражнение (средней сложности): докажите лемму. Указание очень спойлерное.[Указание.]
От противного. Предположим счетное всюду плотное множество в
таки есть. Обозначим его
.
Каждый элемент несчетного множества
можно окружить шаром радиуса
. Множество таких шаров (не пересекающихся), очевидно, несчетно. Покажите, что при выборе достаточно малого
, условие плотности множества
приводит к тому, что в каждом таком шаре должен быть его представитель. При этом множество шаров несчетно, а значит несчетно и
.
Таким образом, чтобы доказать несепарабельность)
, достаточно построить множество
.
Сделаем это, опять, же, на примере
.
Искомым является множество функций&space;=&space;\left&space;|&space;x&space;-c&space;\right&space;|,&space;c\in\left&space;(&space;a,b&space;\right&space;))
. Очевидно, оно несчетно, так как несчетно множество)
.
Почему нам эти функции подходят - ясно из картинки, где я нарисовал две такие функции (синий и зеленый графики) для двух разных параметров, а также модуль их разности (красный график).

Упражнение (несложное): покажите, что,&space;\:&space;c_1\neq&space;c_2.)
Собственно нами доказана в случае
следующая:
Теорема: пространство)
- несепарабельно.
В частности, как я уже говорил, это означает, что в пространстве
есть функции, для которых при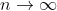
погрешность кусочно-линейной аппроксимации не стремится к нулю.
Чтобы не давиться всухомятку теорией, в следующий раз мы построим пример такой функции, дабы пошшупать ее своими руками и, таки, убедиться на практике, что
- несепрабельно, со всеми вытекающими.
Продолжение.
Предыдущая часть.
Рассматриваем пространство

, оно же

, с нормой:

Сегодня закрываем вопрос с сепарабельностью.
Погнали!
Ситуация с кусочно-линейной аппроксимацией кардинально меняется в случае, когда
.
Напомню, разбиение отрезка
у нас равномерное, на
одинаковых частей.
Введем дополнительно:
Посмотрите на картинку, где я нарисовал тот самый ромбик из самой-самой первой части. Как вы, надеюсь, помните, из-за наложенного на функцию условия Липшица, функция
, с зафиксированными на границах некоего отрезка (в нашем случае, элемента разбиения) значениями, не может покинуть границы небесно-голубого параллелограмма. Дабы не повторяться, я рекомендую тем, для кого этот факт непрозрачен, пройти сюда, где обсуждаются функции с условием Липшица.

Модули угловых коэффициентов прямых, образующих границы ромба, подчинены неравенству:
(Это непосредственно вытеркает из определения нормы
).
Отсюда, просто из элементарной геометрии, следует максимальная оценка погрешности кусочно-линейной аппроксимации в смысле нормы
:
Очень, кстати, удобная оценка, вполне применимая на практике. Еще лучше, если нам известна не только норма целиком, но и вклад второй компоненты (т.е. показатель Липшица). При использовании показателя Липшица вместо нормы данная оценка становится неулучшаемой.
Упражнение (чуть сложнее, чем простое): докажите оценку. Задачка на геометрию, практисски.
Однако, мы таки обсуждаем
, а вовсе не
.
Напомню:
Благодаря полученной выше оценке, имеем:
Как видите, если для второго слагаемого справа можно было также, как для первого, указать подходящую оценку, или хотя бы показать его стремление к нулю при
, то до окончательного доказательства сепарабельности
будет рукой подать.
Если бы... Если...
Короче, прекращаю тянуть резину за хвост в долгий ящик. Петух пропел трижды.
Пространство
не обладает свойством сепарабельности.
Приплыли.
В тот момент, когда во время подготовки очередного поста, вместо ненапряжного доказательства сепарабельности в результате получилось вот ЭТО - шаблон у меня треснул с пушечным грохотом. Неожиданность, да.
Вообще, свойства пространств
и сами они довольно скупо обсуждаются в литературе. А уж вопрос сепарабельности не упоминается вообще ни в одной из книжек, что у меня есть под рукой. Изначально, сепарабельность я хотел рассмотреть чисто для кучи, шоб було. Однако, в результате, это оказалась самой интересной частью работы. Шутка ли, нетривиальное несепарабельное пространство, более того, не искусственный какой случай, любимый лишь специалистами по функциональному анализу, а пространства, которые реально используются, например, в математической физике.
Лемма: если в некотором банаховом пространстве
существует несчетное множество
, такое, что попарные расстояния между его элементами больше некоторой фиксированной константы
, т.е. для любых
справедливо:
то пространство
- несепарабельно.
Упражнение (средней сложности): докажите лемму. Указание очень спойлерное.[Указание.]
От противного. Предположим счетное всюду плотное множество в
таки есть. Обозначим его
.
Каждый элемент несчетного множества
можно окружить шаром радиуса
. Множество таких шаров (не пересекающихся), очевидно, несчетно. Покажите, что при выборе достаточно малого
, условие плотности множества
приводит к тому, что в каждом таком шаре должен быть его представитель. При этом множество шаров несчетно, а значит несчетно и
.
Таким образом, чтобы доказать несепарабельность
, достаточно построить множество
.
Сделаем это, опять, же, на примере
.
Искомым является множество функций
. Очевидно, оно несчетно, так как несчетно множество
.
Почему нам эти функции подходят - ясно из картинки, где я нарисовал две такие функции (синий и зеленый графики) для двух разных параметров, а также модуль их разности (красный график).

Упражнение (несложное): покажите, что
Собственно нами доказана в случае
следующая:
Теорема: пространство
- несепарабельно.
В частности, как я уже говорил, это означает, что в пространстве
есть функции, для которых при
погрешность кусочно-линейной аппроксимации не стремится к нулю.
Чтобы не давиться всухомятку теорией, в следующий раз мы построим пример такой функции, дабы пошшупать ее своими руками и, таки, убедиться на практике, что
- несепрабельно, со всеми вытекающими.
Продолжение.