Ликбез по кватернионам, часть 7: интегрирование угловых скоростей, углы Эйлера-Крылова
Оглавление "Ликбеза по кватернионам":
[Spoiler (click to open)]
Часть 1 - история вопроса
Часть 2 - основные операции
Часть 3 - запись вращения через кватернионы
Часть 4 - кватернионы и спиноры; порядок перемножения
Часть 5 - практическая реализация поворота
Часть 5 1/2 - введение метрики, "расстояния" между поворотами
часть 5 5/8 - метрика ненормированных кватернионов
часть 5 11/16 - красивая псевдометрика произвольных кватернионов
Часть 5 3/4 - исследуем "пространство поворотов"
Часть 5 7/8 - почти изотропный ёжик
Часть 6 - поворот по кратчайшему пути
Часть 6 1/4 - кратчайший поворот в общем случае
Часть 6 2/4 - поворот, совмещающий два направления
Часть 6 3/4 - кватернион из синуса и косинуса угла
Часть 6 7/8 - "уполовинивание угла" на плоскости
Часть 7 - интегрирование угловых скоростей, углы Эйлера-Крылова
Часть 8 - интегрирование угловых скоростей, матрицы поворота
Часть 8 1/2 - ортонормирование матрицы и уравнения Пуассона
Часть 9 - интегрирование угловых скоростей с помощью кватернионов
Часть 10 - интегрирование угловых скоростей, методы 2-го порядка
Часть 10 1/2 - интегрирование с поддержанием нормы
Часть 11 - интегрирование угловых скоростей, методы высших порядков (в разработке)
Часть 12 - навигационная задача
Часть 13 - Дэвенпорт берёт след!
Часть 14 - линейный метод Мортари-Маркли
Часть 15 - среднее от двух кватернионов
Часть 15 1/2 - проверка и усреднение кватернионов
Часть 16 - разложение кватерниона на повороты
Часть 17 - лидарная задача
Задачка к части 17
Дэвенпорт VS Мортари-Маркли
Мортари-Маркли берут реванш!
Дэвенпорт VS Мортари-Маркли, раунд 3
Интегрирование угловых скоростей
Вот мы, наконец, и подобрались к главному назначению кватернионов - к той задаче, которую они выполняют наиболее достойно и где альтернативы им не предвидится.
Для начала мы попинаем дохлую лошадь, в смысле, углы Эйлера и Крылова, надо же понять, что заставило людей изучать и применять такую эзотерическую вещь, как кватернионы (три мнимые единицы, четырёхмерное пространство, половинные углы) - разве нельзя было обойтись курсом-креном-тангажом!?
Задача такова: мы знаем ориентацию нашего изделия в начальный момент времени, и у нас есть датчики угловой скорости (ДУСы). Это могут быть старомодные механические датчики, основанные на гироскопах (именно их неправильно смонтировали на печально известном «Протоне»), либо микроэлектромеханические (MEMS) датчики, либо более точные волоконно-оптические, либо лазерные. Последние два упорно называют гироскопами, и действительно, свет там бежит по кругу, но это название всё равно не вполне корректно. Пользуясь показаниями этих датчиков, мы должны отслеживать, какой именно поворот совершило изделие, иными словами, отслеживать его ориентацию.
Надеемся, что читателю уже понятно, что накапливать углы независимо по каждой из оси датчиков - подход совершенно неверный. Возьмём для примера поворот самолёта, рассмотренный в главе 2.
Первоначально самолёт летел с нулевым креном, тангажом и курсом. Затем он совершил поворот на 90 градусов по крену, после чего на 90 градусов по курсу. Как мы увидели ранее, после этих двух поворотов самолёт начал лететь вертикально вниз, то есть его тангаж стал равен -90°, хотя непосредственно по оси тангажа мы вообще не производили поворотов!
Кроме того, данная ориентация самолёта демонстрирует явление «складывания рамок» или «шарнирного замка». Согласно ГОСТ 20058-80 и аналогичным DIN 9300 и ISO 1151-2:1985, когда мы говорим, что самолёт имеет определенный курс, тангаж и крен, это значит: соответствующая ориентация в пространстве будет достигнута, если мы начнём с горизонтального положения на север, затем повернём самолёт по курсу, вслед за этим - по тангажу и, наконец, по крену (см. рисунок). Когда тангаж равен ±90° (самолёт "смотрит" вертикально вверх или вертикально вниз), курс и крен начинают работать одинаково (курс 0° и крен 90° дадут такое же положение, как и курс 90° и крен 0°, и ещё бесконечно много других комбинаций), что и называется складыванием рамок. Если мы примем, что в данной ориентации курс равен 90°, а крен - нулю (именно так рекомендуется разрешать неоднозначность), то сколько угодно малый поворот самолёта по курсу (в смысле, в сторону крыла, т.е при работе рулём направления) заставит скачкообразно изменить показания курса до 0°, крена - до 90°, а тангаж уменьшится на этот самый малый поворот. «Скачкообразно» означает бесконечную производную в этой точке - а это явно нехорошо…
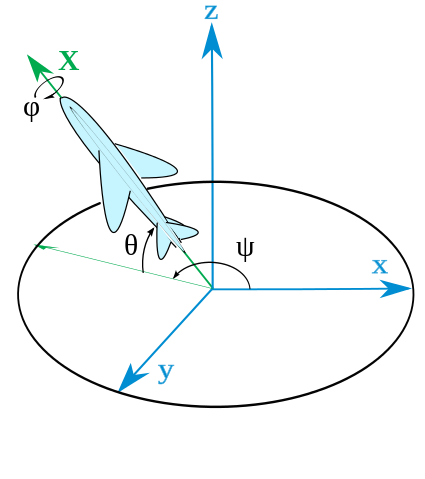
Ещё одно неожиданное препятствие: в книгах по теоретической механике рассматриваются углы Эйлера и углы Крылова. Углы Эйлера носят имена: прецессия, нутация, собственное вращение - они нашли своё применение в описании быстро вращающихся штук.
Углы Крылова: рысканье, дифферент, крен. Рысканье - то же самое, что курс, дифферент - это морской термин для тангажа. Кажется, что знакомые нам курс-тангаж-крен - это и есть углы Крылова.
Не тут-то было.
Вот как определены углы Крылова:

(боролся с искушением прифотошопить сюда лебедя, рака и щуку, тянущих в трёх взаимно-перпендикулярных направлениях)
Приведём цитату из книги Бранца В.Н. и Шмыглевского И.П. - Применение кватернионов в задачах ориентации твердого тела (1973), стр. 79:
Первый поворот выполняется вокруг оси i3 на угол курса φ, второй поворот происходит по оси i`2 на угол крена ψ и третий - вокруг оси e1 на угол тангажа ϑ.
Мы можем заметить, что повороты производятся не в том порядке, как указано ранее. Определённые таким способом углы тоже имеют право на существование, и при малых отклонениях крена и тангажа не будут отличаться от ранее введенных, но уже при углах, характерных для самолётов гражданской авиации, разница будет заметна.
Возьмём всё-таки «вырожденный» пример - самолёт полетел вверх ногами, при этом, чтобы не свалиться, немного задрал нос вверх. Когда мы опишем положение самолёта через углы Крылова, окажется, что самолёт летит с отрицательным тангажом, ведь первым осуществляется поворот по крену, а только потом - на перевёрнутом самолёте - поворот по тангажу, из-за чего он и должен поменять знак - именно в этом случае нос задерётся вверх.
Однако ГОСТ 20058-80 «ДИНАМИКА ЛЕТАТЕЛЬНЫХ АППАРАТОВ В АТМОСФЕРЕ» (http://docs.cntd.ru/document/gost-20058-80 ) даёт несколько иное определение тангажа:
26. Угол тангажа ϑ - угол между продольной осью OX и горизонтальной плоскостью OXgZg нормальной системы координат.
То есть, когда нос смотрит вверх, тангаж всегда должен получаться положительным, без разницы, как накренён самолёт!
Даже при достаточно плавных разворотах, такая взаимозависимость углов проявится, что приведёт к ошибочному восприятию ориентации объекта в пространстве.
Да и в целом кинематические уравнения для углов не очень радостны. Приведём их для углов Эйлера и для угловых скоростей, измеренных в связанном базисе (то есть, датчики стоят на объекте и поворачиваются вместе с ним):
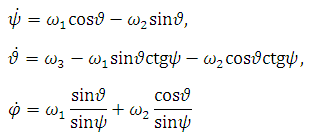
Разумеется, для работы с углами тангажа, курса и крена, описанными в ГОСТ 20058-80, эти формулы не годятся - нужно вывести другие. Оставим это в качестве упражнения для самых упорных читателей.
В описании ориентации твёрдого тела в виде трёх углов есть определённые преимущества:
- оно наиболее компактно, требуя лишь 3 числа,
- более-менее понятно человеку,
- иногда позволяет найти аналитическое решение кинематических уравнений - для этого Эйлер свои углы и вводил когда-то.
Всё остальное - недостатки: многоэтажные формулы с множеством тригонометрических функций, появление особых точек, в которых нужно ставить свои «костыли» или заранее сдаться, сказав - сюда не заходите, иначе мы потеряемся в пространстве! Ещё мы можем заметить, что все углы способны неограниченно расти, поэтому неплохо бы каждый из них держать в разумных рамках, прибавляя или вычитая 2π, когда понадобится. Для тангажа и вовсе неплохо бы ограничиться -π .. π, что требует коррекции не только самого тангажа, но и курса. Практически любая работа с тремя углами сложна - поворот векторов, сравнение двух положений, композиция поворотов и пр. - везде мы натыкаемся на двухэтажные выражения и особые точки.
Углы Эйлера или Крылова (или какие-либо другие) никогда на практике не использовались в бесплатформенных системах ориентации, но неявным образом участвовали в работе гироплатформ. По сути, гироплатформа - это датчик, который возвращает ориентацию аппарата в пространстве сразу же в виде углов, а в качестве бонуса интегрирующая ускорения, спроецированные на неподвижные оси! Особые точки «математики» здесь соответствовали особым точкам «в железе» - складыванию рамок, если только не предпринимались специальные шаги, такие как введение четвёртой (избыточной) рамки или и вовсе отказ от рамок в пользу вложенных сфер.
Два других представления поворота твёрдого тела - через матрицы поворота и через кватернионы - свободны от недостатков трёх углов. Все операции оказываются линейными, особых точек нет. Продолжение следует...
PS. Поздравим с днём рождения heana_costre, звездочёта, одну из постоянных читательниц этого "талмуда" про кватернионы!
[Spoiler (click to open)]
Часть 1 - история вопроса
Часть 2 - основные операции
Часть 3 - запись вращения через кватернионы
Часть 4 - кватернионы и спиноры; порядок перемножения
Часть 5 - практическая реализация поворота
Часть 5 1/2 - введение метрики, "расстояния" между поворотами
часть 5 5/8 - метрика ненормированных кватернионов
часть 5 11/16 - красивая псевдометрика произвольных кватернионов
Часть 5 3/4 - исследуем "пространство поворотов"
Часть 5 7/8 - почти изотропный ёжик
Часть 6 - поворот по кратчайшему пути
Часть 6 1/4 - кратчайший поворот в общем случае
Часть 6 2/4 - поворот, совмещающий два направления
Часть 6 3/4 - кватернион из синуса и косинуса угла
Часть 6 7/8 - "уполовинивание угла" на плоскости
Часть 7 - интегрирование угловых скоростей, углы Эйлера-Крылова
Часть 8 - интегрирование угловых скоростей, матрицы поворота
Часть 8 1/2 - ортонормирование матрицы и уравнения Пуассона
Часть 9 - интегрирование угловых скоростей с помощью кватернионов
Часть 10 - интегрирование угловых скоростей, методы 2-го порядка
Часть 10 1/2 - интегрирование с поддержанием нормы
Часть 11 - интегрирование угловых скоростей, методы высших порядков (в разработке)
Часть 12 - навигационная задача
Часть 13 - Дэвенпорт берёт след!
Часть 14 - линейный метод Мортари-Маркли
Часть 15 - среднее от двух кватернионов
Часть 15 1/2 - проверка и усреднение кватернионов
Часть 16 - разложение кватерниона на повороты
Часть 17 - лидарная задача
Задачка к части 17
Дэвенпорт VS Мортари-Маркли
Мортари-Маркли берут реванш!
Дэвенпорт VS Мортари-Маркли, раунд 3
Интегрирование угловых скоростей
Вот мы, наконец, и подобрались к главному назначению кватернионов - к той задаче, которую они выполняют наиболее достойно и где альтернативы им не предвидится.
Для начала мы попинаем дохлую лошадь, в смысле, углы Эйлера и Крылова, надо же понять, что заставило людей изучать и применять такую эзотерическую вещь, как кватернионы (три мнимые единицы, четырёхмерное пространство, половинные углы) - разве нельзя было обойтись курсом-креном-тангажом!?
Задача такова: мы знаем ориентацию нашего изделия в начальный момент времени, и у нас есть датчики угловой скорости (ДУСы). Это могут быть старомодные механические датчики, основанные на гироскопах (именно их неправильно смонтировали на печально известном «Протоне»), либо микроэлектромеханические (MEMS) датчики, либо более точные волоконно-оптические, либо лазерные. Последние два упорно называют гироскопами, и действительно, свет там бежит по кругу, но это название всё равно не вполне корректно. Пользуясь показаниями этих датчиков, мы должны отслеживать, какой именно поворот совершило изделие, иными словами, отслеживать его ориентацию.
Надеемся, что читателю уже понятно, что накапливать углы независимо по каждой из оси датчиков - подход совершенно неверный. Возьмём для примера поворот самолёта, рассмотренный в главе 2.
Первоначально самолёт летел с нулевым креном, тангажом и курсом. Затем он совершил поворот на 90 градусов по крену, после чего на 90 градусов по курсу. Как мы увидели ранее, после этих двух поворотов самолёт начал лететь вертикально вниз, то есть его тангаж стал равен -90°, хотя непосредственно по оси тангажа мы вообще не производили поворотов!
Кроме того, данная ориентация самолёта демонстрирует явление «складывания рамок» или «шарнирного замка». Согласно ГОСТ 20058-80 и аналогичным DIN 9300 и ISO 1151-2:1985, когда мы говорим, что самолёт имеет определенный курс, тангаж и крен, это значит: соответствующая ориентация в пространстве будет достигнута, если мы начнём с горизонтального положения на север, затем повернём самолёт по курсу, вслед за этим - по тангажу и, наконец, по крену (см. рисунок). Когда тангаж равен ±90° (самолёт "смотрит" вертикально вверх или вертикально вниз), курс и крен начинают работать одинаково (курс 0° и крен 90° дадут такое же положение, как и курс 90° и крен 0°, и ещё бесконечно много других комбинаций), что и называется складыванием рамок. Если мы примем, что в данной ориентации курс равен 90°, а крен - нулю (именно так рекомендуется разрешать неоднозначность), то сколько угодно малый поворот самолёта по курсу (в смысле, в сторону крыла, т.е при работе рулём направления) заставит скачкообразно изменить показания курса до 0°, крена - до 90°, а тангаж уменьшится на этот самый малый поворот. «Скачкообразно» означает бесконечную производную в этой точке - а это явно нехорошо…

Ещё одно неожиданное препятствие: в книгах по теоретической механике рассматриваются углы Эйлера и углы Крылова. Углы Эйлера носят имена: прецессия, нутация, собственное вращение - они нашли своё применение в описании быстро вращающихся штук.
Углы Крылова: рысканье, дифферент, крен. Рысканье - то же самое, что курс, дифферент - это морской термин для тангажа. Кажется, что знакомые нам курс-тангаж-крен - это и есть углы Крылова.
Не тут-то было.
Вот как определены углы Крылова:

(боролся с искушением прифотошопить сюда лебедя, рака и щуку, тянущих в трёх взаимно-перпендикулярных направлениях)
Приведём цитату из книги Бранца В.Н. и Шмыглевского И.П. - Применение кватернионов в задачах ориентации твердого тела (1973), стр. 79:
Первый поворот выполняется вокруг оси i3 на угол курса φ, второй поворот происходит по оси i`2 на угол крена ψ и третий - вокруг оси e1 на угол тангажа ϑ.
Мы можем заметить, что повороты производятся не в том порядке, как указано ранее. Определённые таким способом углы тоже имеют право на существование, и при малых отклонениях крена и тангажа не будут отличаться от ранее введенных, но уже при углах, характерных для самолётов гражданской авиации, разница будет заметна.
Возьмём всё-таки «вырожденный» пример - самолёт полетел вверх ногами, при этом, чтобы не свалиться, немного задрал нос вверх. Когда мы опишем положение самолёта через углы Крылова, окажется, что самолёт летит с отрицательным тангажом, ведь первым осуществляется поворот по крену, а только потом - на перевёрнутом самолёте - поворот по тангажу, из-за чего он и должен поменять знак - именно в этом случае нос задерётся вверх.
Однако ГОСТ 20058-80 «ДИНАМИКА ЛЕТАТЕЛЬНЫХ АППАРАТОВ В АТМОСФЕРЕ» (http://docs.cntd.ru/document/gost-20058-80 ) даёт несколько иное определение тангажа:
26. Угол тангажа ϑ - угол между продольной осью OX и горизонтальной плоскостью OXgZg нормальной системы координат.
То есть, когда нос смотрит вверх, тангаж всегда должен получаться положительным, без разницы, как накренён самолёт!
Даже при достаточно плавных разворотах, такая взаимозависимость углов проявится, что приведёт к ошибочному восприятию ориентации объекта в пространстве.
Да и в целом кинематические уравнения для углов не очень радостны. Приведём их для углов Эйлера и для угловых скоростей, измеренных в связанном базисе (то есть, датчики стоят на объекте и поворачиваются вместе с ним):
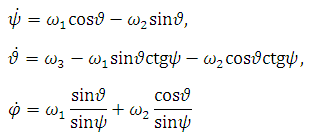
Разумеется, для работы с углами тангажа, курса и крена, описанными в ГОСТ 20058-80, эти формулы не годятся - нужно вывести другие. Оставим это в качестве упражнения для самых упорных читателей.
В описании ориентации твёрдого тела в виде трёх углов есть определённые преимущества:
- оно наиболее компактно, требуя лишь 3 числа,
- более-менее понятно человеку,
- иногда позволяет найти аналитическое решение кинематических уравнений - для этого Эйлер свои углы и вводил когда-то.
Всё остальное - недостатки: многоэтажные формулы с множеством тригонометрических функций, появление особых точек, в которых нужно ставить свои «костыли» или заранее сдаться, сказав - сюда не заходите, иначе мы потеряемся в пространстве! Ещё мы можем заметить, что все углы способны неограниченно расти, поэтому неплохо бы каждый из них держать в разумных рамках, прибавляя или вычитая 2π, когда понадобится. Для тангажа и вовсе неплохо бы ограничиться -π .. π, что требует коррекции не только самого тангажа, но и курса. Практически любая работа с тремя углами сложна - поворот векторов, сравнение двух положений, композиция поворотов и пр. - везде мы натыкаемся на двухэтажные выражения и особые точки.
Углы Эйлера или Крылова (или какие-либо другие) никогда на практике не использовались в бесплатформенных системах ориентации, но неявным образом участвовали в работе гироплатформ. По сути, гироплатформа - это датчик, который возвращает ориентацию аппарата в пространстве сразу же в виде углов, а в качестве бонуса интегрирующая ускорения, спроецированные на неподвижные оси! Особые точки «математики» здесь соответствовали особым точкам «в железе» - складыванию рамок, если только не предпринимались специальные шаги, такие как введение четвёртой (избыточной) рамки или и вовсе отказ от рамок в пользу вложенных сфер.
Два других представления поворота твёрдого тела - через матрицы поворота и через кватернионы - свободны от недостатков трёх углов. Все операции оказываются линейными, особых точек нет. Продолжение следует...
PS. Поздравим с днём рождения heana_costre, звездочёта, одну из постоянных читательниц этого "талмуда" про кватернионы!