Квантовый ликбез - 15. Седьмой постулат.
Предыдущие посты
Продолжаем разбираться с квантовой корреляцией.
В прошлой части мы "провели" классический эксперимент (рисунок 14.2). Напомню, там у нас тело с нулевым моментом импульса разваливается на две части так, что каждая часть вращается. Измеряя затем моменты импульсов обеих частей, мы видим, что они строго коррелируют (равны по величине и противоположны по направлению). Мы говорили о том, что это "программный" тип корреляции. Резонно считать, что эта программа корреляции «запускается» в момент рождения коррелирующей пары тел, то есть, в момент развала исходного тела. Действительно, при возникновении пары моменты импульсов обеих частей однозначно определяются. Причём не абы как, а так, что в сумме их значения дают ноль, в полном соответствии с законом сохранения момента импульса. И далее, благодаря тому же закону, эти значения не изменяются, если, конечно, на тела никак не воздействовать. По-другому можно сказать так: в момент рождения пары возникает физическое состояние корреляции двух частиц.
Вплоть до четырнадцатой части ликбеза мы работали с состояниями одиночных тел или частиц. Такие «автономные» состояния мы рассматривали как определённые значения (для классических тел) или бесконечные наборы значений (для квантовых частиц) связанных с объектом физических величин: координаты, импульса и так далее. Но теперь такой номер не пройдёт. При исследовании явления корреляции мы должны рассматривать состояние системы в целом. В разбираемом случае для нас важны не только и не столько «автономные» значения моментов импульса левого и правого тела, сколько их взаимная комбинация, то есть - системное состояние. Так вот, в результате действия закона сохранения момента импульса, тут возможны только такие системные состояния, в которых моменты импульса тел противоположны.
Возвращаемся в квантовый мир. Всё, что мы до этого говорили в нашем ликбезе об автономных квантовых состояниях, в полной мере справедливо и для системных квантовых состояний. Например, для одиночной частицы мы рассматривали спин как бесконечную совокупность различных виртуальных классических значений момента импульса. И говорили, что разные виртуальные значения момента импульса - это разные варианты будущего, в смысле, разные результаты предстоящего измерения момента импульса одиночной частицы.
Но когда речь идёт о системе из двух квантовых частиц, мы должны также рассматривать как разные виртуальные варианты будущего разные попарные комбинации классических моментов импульса.
И также как в автономном случае, каждая виртуальная комбинация обладает своим квантовым вектором.
И также виртуальные комбинации объединяются в группы по возможному результату будущего измерения.
И также квантовые вектора комбинированных виртуальных вариантов одной группы «вступают» в суперпозицию и образуют групповой вектор - амплитуду вероятности. Кстати, важно понимать, что в общем случае амплитуда вероятности комбинации значений не зависит от амплитуд вероятности автономных значений (не пугайтесь, разъяснение этой заумной фразы чуть ниже будет).
И также амплитуда вероятности определяет вероятность реализации виртуальных классических комбинаций из соответствующей группы. Если амплитуда вероятности группы равна нулю - то комбинации этой группы нереализуемы.
Короче говоря, системные виртуальные варианты являются такими же реальными физическими объектами, как и автономные виртуальные варианты.
Так вот, вселенная устроена таким образом, что реализуемыми могут быть только такие виртуальные комбинации значений физических величин, которые не противоречат классическим законам физики.
В частности, в опыте с двумя братьями-фермионами, который мы рассматривали в прошлой части, реализуемы только такие комбинации результатов измерений, которые не противоречат классическому закону сохранения момента импульса.
Хотя, тут ещё большой вопрос, «кто на ком стоял». Скорее, наоборот, классические законы физики являются следствием причудливой игры квантовых векторов. В десятой части было показано, как из вращения квантовых векторов виртуальных состояний получается классическое прямолинейное движение свободной частицы. Аналогично можно было бы показать, как суперпозиция квантовых векторов формирует законы сохранения, но тут мы не станем тратить усилия на это весьма громоздкое занятие.
Давайте лучше ещё раз посмотрим на опыт с парой запутанных фермионов (рисунок 15.1).
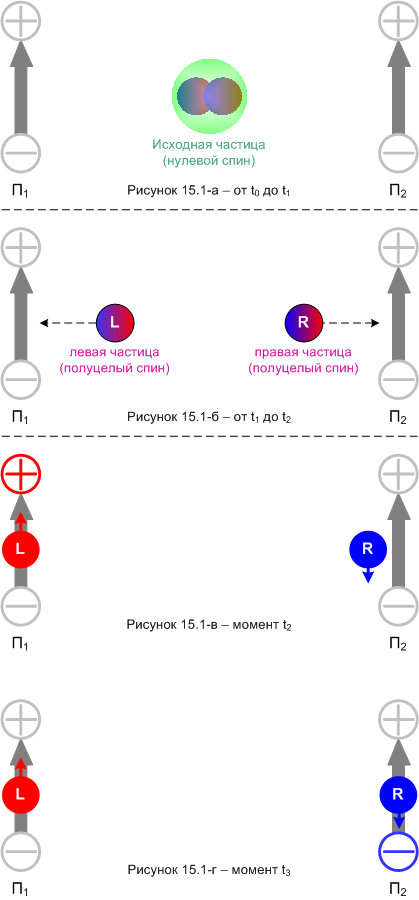
Чтобы легче было ориентироваться в том, что здесь происходит, на рисунке обозначены различные моменты времени:
t0 - время начала опыта, когда мы помещаем в установку исходную частицу;
t1 - время распада исходной частицы на пару фермионов;
t2 - время измерения момента импульса левой частицы прибором П1;
t3 - время измерения момента импульса правой частицы прибором П2.
Теперь внимательно. В момент t1 рождается квантовая система, состоящая из двух запутанных фермионов. До первого измерения, момента t2, система находится в состоянии неопределённости - может быть получен любой из реализуемых вариантов. Это касается и состояния левой частицы, и состояния правой частицы, а также состояния системы частиц в целом. Определённым является только то, что комбинаций результатов 〈+L;+R〉 или 〈-L;-R〉 мы здесь точно не получим. Но вот в момент t2 мы измеряем момент импульса левой частицы и получаем результат, например, 〈+L〉. Согласно шестому постулату, квантовая редукция уменьшает неопределённость состояния системы ровно на ту долю информации, которую нам удалось «извлечь». И уменьшается она так: все варианты, которые противоречат полученной информации, становятся нереализуемыми.
Если говорить только о вариантах будущего левой частицы, то невозможным становится результат измерения 〈-L〉. В смысле, если мы ещё раз измерим момент импульса левой частицы тем же самым прибором П1 или любым другим прибором с аналогичном собственным направлением, то мы гарантированно получим тот же результат, что и при первом измерении, то есть 〈+L〉.
Если же говорить о системном состоянии, то тут в качестве вариантов будущего рассматриваются комбинации результатов двух измерений - левой и правой частицы. Левую частицу мы уже измерили и получили результат 〈+L〉. Если бы мы имели дело с парой случайных, независимых частиц, то мы имели бы уже «половину» информации о системном состоянии, и квантовая редукция из четырёх групп оставила бы реализуемыми только две: |+L;+R〉 и |+L;-R〉. Но наши частицы запутаны законом сохранения момента импульса, и мы в курсе, что варианты группы |+L;+R〉 также нереализуем. Он был таковыми до первого измерения, таковым и остался. Остаётся единственная группа реализуемых виртуальных комбинаций: |+L;-R〉. А если осталась одна группа, значит, никакой неопределённости не осталось, будущее правой частицы теперь тоже предрешено: при измерении на приборе П2 в момент t3 мы определённо получим результат 〈-R 〉, что на деле всегда и происходит.
Вот теперь, пожалуй, пора раскрыть секрет нелокальности квантовых корреляций. Вот он, этот
секрет:
Постулат 7. Реализация виртуального варианта осуществляется задним числом, от момента возникновения варианта.
Поясним это на примере нашего опыта. В момент времени t1 у нас появляются четыре группы системных виртуальных вариантов, две из которых реализуемы. Значит, момент t1 можно считать точкой "развилки", отсюда берут старт разные альтернативы будущего и начинается неопределённость. Но после первого же измерения в момент t2 все неопределённости, возникшие в момент t1, "разрешаются". И всё теперь выглядит таким образом, как будто бы никакой неопределённости и не существовало вовсе. Как будто бы единственная реализуемая комбинация результатов возникла уже в момент t1. Как будто бы мы имели дело не с квантовой, а классической системой частиц.
Вот вам аналогия для прояснения седьмого постулата. Предположим, перед вами ветвистое дерево. Вы случайно выбираете одну веточку и дергаете за неё. Но тонкая ветка сидит прочно! Рывок передаётся более толстой "материнской" ветке, затем ещё более толстой и так до самого ствола. У ствола толстая ветка обламывается, и в итоге у вас в руках не одна веточка, а целый куст. Теперь просто сопоставим это с нашим опытом. Маленькие «веточки» дерева виртуальной реальности - это группы автономных виртуальных вариантов |+L〉, |-L〉, |+R〉, |- R〉. Толстые ветки - это группы виртуальных комбинаций |+L;+R〉, |+L;-R〉, |-L;+R〉, |-L;-R〉. На рисунках 15.2 я попытался изобразить всю эту «ботанику» в виде временных диаграмм. Вот на рисунке 15.2-а картина квантовой реальности перед первым измерением.
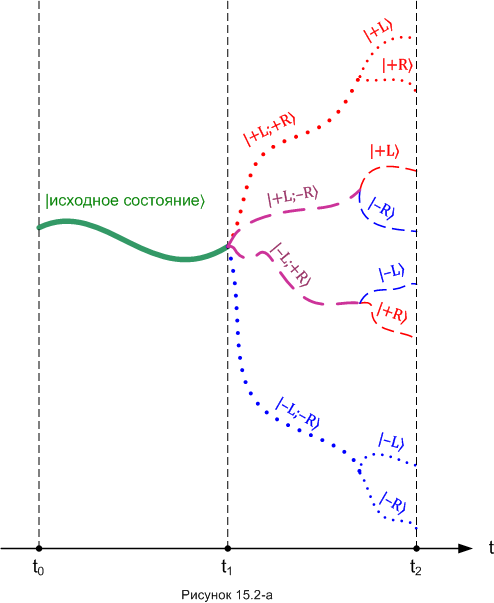
Нереализуемые группы обозначены пунктирными линиями. Реализуемые - штриховыми линиями.
На рисунке 15.2-б показан момент первого измерения - в момент t2 мы «дёргаем за веточку»,
тянем её из виртуальной реальности в классическую реальность, и видим, что это веточка 〈+L〉.
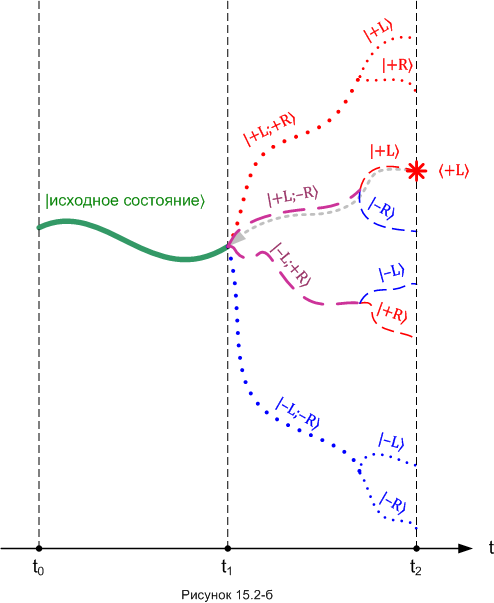
Но веточка |+L〉 в нашем эксперименте «намертво» запутана с веточкой |-R〉, вместе они образуют толстую ветку |+L;-R〉. Стало быть, наше измерение выдирает из квантовой реальности всю толстую ветку, которая «растёт» от момента времени t1. Это и есть «работа» седьмого постулата: измеряем мы в момент t2, но реализация варианта, ставшего результатом, происходит в прошлом, в момент t1. Рисунок 15.2-в иллюстрирует состояние системы после t2. Бывшая (до первого измерения) виртуальная ветка |+L;-R〉 показана сплошной линией, потому что теперь (после первого измерения) она стала бывшим классическим, то есть, единственно возможным вариантом. А если этот теперь классический вариант реализовался в тот момент, когда образовалась пара частиц, то и результат второго измерения 〈-R〉 теперь задним числом предопределён.
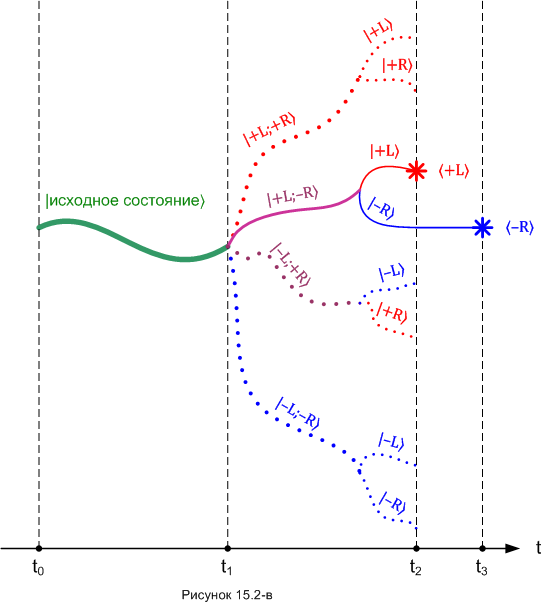
Как видите, такой механизм вполне объясняет квантовую корреляцию и при этом никакого канала нелокальной «суперсвязи» между частицами не требует.
Зато седьмой постулат требует другого странного явления, согласиться с которым "здравому смыслу" очень трудно. Ведь здесь, как ни крути, происходит обратный скачок во времени от момента измерения к моменту развилки вариантов и изменение прошлого. Но, друзья мои, вы ведь уже согласились (надеюсь) с существованием ненаблюдаемой квантовой реальности, битком набитой виртуальными вариантами будущего. Так сделайте следующий шаг и согласитесь с тем, что в квантовой реальности возможен также виртуальный отскок во времени. А "здравому смыслу" передайте, чтобы он не беспокоился: ни к каким временным парадоксам в классической реальности такие возвраты в прошлое не приводит. Ведь эти возвраты сугубо виртуальны, и использовать их для реальных путешествий во времени никак не получится. Зато, зная о их существовании, легко объяснить механизм квантовой нелокальности (надеюсь, мне это удалось), эксперименты с отложенным выбором и квантовую телепортацию (эти объяснения ещё впереди).
В защиту справедливости седьмого постулата, расскажу ещё вот что. Здесь уже не раз виртуальные варианты квантовой реальности сопоставлялись с мыслями в голове (вспомните притчу про буриданова осла в пятой части). Можно это сделать и сейчас: мысленно, то есть - виртуально, мы легко путешествуем в прошлое. Мы это делаем всякий раз, когда что-нибудь вспоминаем. Что, хотите возразить, что такие мысленные скачки не меняют, мол, прошлое? Да как сказать! Представьте себе: вы проснулись утром, позавтракали, пошли на работу. Всё как всегда, обычное утро, через неделю-другую оно потерялось бы в прошлом среди таких же обыденных утр (или утер?). Но этим же днём с вами вдруг случилось какое-то очень волнующее событие. Клад нашли, например, или влюбились с первого взгляда. И сразу же это утро перестанет быть обычным. Все сегодняшние утренние мелочи теперь, задним числом, обретут для вас значение предзнаменований и навсегда врежутся в память. Почему же обычное, уже прошедшее утро стало вдруг особенным? Потому что вы под впечатлением события совершили виртуальный мысленный возврат во времени и задним числом наполнили утро этого дня особым смыслом.
Как, ваш "здравый смысл" до сих протестует? Тогда приведу самый, как мне кажется, веский довод.
Проведём следующий мысленный эксперимент. Одну частицу скоррелированной пары отдаём Алисе, вторую отдаём Бобу. Алиса и Боб сверяют часы и, каждый со своей частицей, разъёзжаются на достаточно далёкое расстояние. Допустим, Алиса едет на Северный полюс, а Боб - на Южный.
Одновременно, в оговоренный момент времени, Алиса и Боб измеряют спины своих частиц. Ну как одновременно? Сколь бы не были точны их часы, на практике какое-то расхождение, пусть на миллионную, пусть на триллионную долю секунды, будет. И всё равно получится, что кто-то из них измерит чуть раньше. Пусть первой будет Алиса.
Мы помним, что до измерения обе частицы ЭПР-пары находятся в неопределённом состоянии. Но как только Алиса проведёт измерение, её частица переходит в какое-то определённое состояние. Но не только, частица Боба тоже "автоматом" определяется. Казалось бы, вполне резонно думать, что результат Алисы является причиной, а результат Боба - следствием.
Однако не будем забывать о "фокусах" специальной теории относительности, где понятия "раньше" и "позже" вовсе не абсолютны. Если события "А" и "Б" происходят в разных точках пространства, то в одной системе отсчёта события "А" и "Б" могут произойти одновременно. В другой "А" происходит раньше "В". В третьей, наоборот, раньше происходит "В".
Так вот, мы условились, что в системе отсчёта, относительно которой оба экспериментатора неподвижны, Алиса измеряет на мгновение раньше Боба. Но, согласно теории относительности, существуют и такие системы отсчёта, где первым измеряет Боб. И мы вынуждены считать, что в этих системах отсчёта следствие (результат Боба) происходит раньше причины (результат Алисы). А это тоже отскок по времени, как не крути.
Вот, теперь хоть отвергаем седьмой постулат, хоть принимаем. Так или иначе, мы вынуждены допускать возможность отскока в прошлое. Но отскок отскоку рознь! Согласно той же теории относительности, если событие "А" является причиной, а событие "В" - следствием, тогда "А" происходит раньше в любой системе отсчёта. Теперь давайте посмотрим, как у нас с этим правилом.
В первом случае (принимаем постулат) отскок происходит в квантовой реальности. Не важно при этом, кто стал инициатором отскока, Алиса или Боб. До измерения оба они, и любой внешний наблюдатель, существуют в реальности, где спины частиц не определены. А после первого измерения эта реальность просто стирается и подменяется на такую, в которой спины определены. Причём, стирается "задним числом". В этой новой реальности ни результат Алисы, ни результат Боба уже не являются причиной. Оба результата - следствие прошлого события, а именно рождения квантово запутанной пары частиц. Таким образом, в обновившейся реальности ни для какого из наблюбателей не существует абсурдной ситуации "следствие опержает причину".
Во втором случае (отвергаем постулат) никакого стирания несостоявшихся виртуальных реальностей не происходит, следствие, получается, предшествует причине в самом что ни на есть классическом смысле. Тогда мы должны признать, что теория относительности в какой-то части "врёт". Лично мне такой подход не кажется состоятельным, так что предлагаю всё же принять седьмой постулат.
Ура! Все восемь постулатов квантовой философии (напомню, что отсчёт начался с нуля) теперь озвучены и разобраны. В следующей части мы рассмотрим некоторые вопросы, которые пока что оставались "за кадром" ликбеза. И заодно немного расширим математический аппарат, с которым мы начали знакомиться в части 12. Этот "аппарат" нам очень понадобится дальше, когда мы будем осваивать принцип действия квантового компьютера.
Продолжение
Продолжаем разбираться с квантовой корреляцией.
В прошлой части мы "провели" классический эксперимент (рисунок 14.2). Напомню, там у нас тело с нулевым моментом импульса разваливается на две части так, что каждая часть вращается. Измеряя затем моменты импульсов обеих частей, мы видим, что они строго коррелируют (равны по величине и противоположны по направлению). Мы говорили о том, что это "программный" тип корреляции. Резонно считать, что эта программа корреляции «запускается» в момент рождения коррелирующей пары тел, то есть, в момент развала исходного тела. Действительно, при возникновении пары моменты импульсов обеих частей однозначно определяются. Причём не абы как, а так, что в сумме их значения дают ноль, в полном соответствии с законом сохранения момента импульса. И далее, благодаря тому же закону, эти значения не изменяются, если, конечно, на тела никак не воздействовать. По-другому можно сказать так: в момент рождения пары возникает физическое состояние корреляции двух частиц.
Вплоть до четырнадцатой части ликбеза мы работали с состояниями одиночных тел или частиц. Такие «автономные» состояния мы рассматривали как определённые значения (для классических тел) или бесконечные наборы значений (для квантовых частиц) связанных с объектом физических величин: координаты, импульса и так далее. Но теперь такой номер не пройдёт. При исследовании явления корреляции мы должны рассматривать состояние системы в целом. В разбираемом случае для нас важны не только и не столько «автономные» значения моментов импульса левого и правого тела, сколько их взаимная комбинация, то есть - системное состояние. Так вот, в результате действия закона сохранения момента импульса, тут возможны только такие системные состояния, в которых моменты импульса тел противоположны.
Возвращаемся в квантовый мир. Всё, что мы до этого говорили в нашем ликбезе об автономных квантовых состояниях, в полной мере справедливо и для системных квантовых состояний. Например, для одиночной частицы мы рассматривали спин как бесконечную совокупность различных виртуальных классических значений момента импульса. И говорили, что разные виртуальные значения момента импульса - это разные варианты будущего, в смысле, разные результаты предстоящего измерения момента импульса одиночной частицы.
Но когда речь идёт о системе из двух квантовых частиц, мы должны также рассматривать как разные виртуальные варианты будущего разные попарные комбинации классических моментов импульса.
И также как в автономном случае, каждая виртуальная комбинация обладает своим квантовым вектором.
И также виртуальные комбинации объединяются в группы по возможному результату будущего измерения.
И также квантовые вектора комбинированных виртуальных вариантов одной группы «вступают» в суперпозицию и образуют групповой вектор - амплитуду вероятности. Кстати, важно понимать, что в общем случае амплитуда вероятности комбинации значений не зависит от амплитуд вероятности автономных значений (не пугайтесь, разъяснение этой заумной фразы чуть ниже будет).
И также амплитуда вероятности определяет вероятность реализации виртуальных классических комбинаций из соответствующей группы. Если амплитуда вероятности группы равна нулю - то комбинации этой группы нереализуемы.
Короче говоря, системные виртуальные варианты являются такими же реальными физическими объектами, как и автономные виртуальные варианты.
Так вот, вселенная устроена таким образом, что реализуемыми могут быть только такие виртуальные комбинации значений физических величин, которые не противоречат классическим законам физики.
В частности, в опыте с двумя братьями-фермионами, который мы рассматривали в прошлой части, реализуемы только такие комбинации результатов измерений, которые не противоречат классическому закону сохранения момента импульса.
Хотя, тут ещё большой вопрос, «кто на ком стоял». Скорее, наоборот, классические законы физики являются следствием причудливой игры квантовых векторов. В десятой части было показано, как из вращения квантовых векторов виртуальных состояний получается классическое прямолинейное движение свободной частицы. Аналогично можно было бы показать, как суперпозиция квантовых векторов формирует законы сохранения, но тут мы не станем тратить усилия на это весьма громоздкое занятие.
Давайте лучше ещё раз посмотрим на опыт с парой запутанных фермионов (рисунок 15.1).

Чтобы легче было ориентироваться в том, что здесь происходит, на рисунке обозначены различные моменты времени:
t0 - время начала опыта, когда мы помещаем в установку исходную частицу;
t1 - время распада исходной частицы на пару фермионов;
t2 - время измерения момента импульса левой частицы прибором П1;
t3 - время измерения момента импульса правой частицы прибором П2.
Теперь внимательно. В момент t1 рождается квантовая система, состоящая из двух запутанных фермионов. До первого измерения, момента t2, система находится в состоянии неопределённости - может быть получен любой из реализуемых вариантов. Это касается и состояния левой частицы, и состояния правой частицы, а также состояния системы частиц в целом. Определённым является только то, что комбинаций результатов 〈+L;+R〉 или 〈-L;-R〉 мы здесь точно не получим. Но вот в момент t2 мы измеряем момент импульса левой частицы и получаем результат, например, 〈+L〉. Согласно шестому постулату, квантовая редукция уменьшает неопределённость состояния системы ровно на ту долю информации, которую нам удалось «извлечь». И уменьшается она так: все варианты, которые противоречат полученной информации, становятся нереализуемыми.
Если говорить только о вариантах будущего левой частицы, то невозможным становится результат измерения 〈-L〉. В смысле, если мы ещё раз измерим момент импульса левой частицы тем же самым прибором П1 или любым другим прибором с аналогичном собственным направлением, то мы гарантированно получим тот же результат, что и при первом измерении, то есть 〈+L〉.
Если же говорить о системном состоянии, то тут в качестве вариантов будущего рассматриваются комбинации результатов двух измерений - левой и правой частицы. Левую частицу мы уже измерили и получили результат 〈+L〉. Если бы мы имели дело с парой случайных, независимых частиц, то мы имели бы уже «половину» информации о системном состоянии, и квантовая редукция из четырёх групп оставила бы реализуемыми только две: |+L;+R〉 и |+L;-R〉. Но наши частицы запутаны законом сохранения момента импульса, и мы в курсе, что варианты группы |+L;+R〉 также нереализуем. Он был таковыми до первого измерения, таковым и остался. Остаётся единственная группа реализуемых виртуальных комбинаций: |+L;-R〉. А если осталась одна группа, значит, никакой неопределённости не осталось, будущее правой частицы теперь тоже предрешено: при измерении на приборе П2 в момент t3 мы определённо получим результат 〈-R 〉, что на деле всегда и происходит.
Вот теперь, пожалуй, пора раскрыть секрет нелокальности квантовых корреляций. Вот он, этот
секрет:
Постулат 7. Реализация виртуального варианта осуществляется задним числом, от момента возникновения варианта.
Поясним это на примере нашего опыта. В момент времени t1 у нас появляются четыре группы системных виртуальных вариантов, две из которых реализуемы. Значит, момент t1 можно считать точкой "развилки", отсюда берут старт разные альтернативы будущего и начинается неопределённость. Но после первого же измерения в момент t2 все неопределённости, возникшие в момент t1, "разрешаются". И всё теперь выглядит таким образом, как будто бы никакой неопределённости и не существовало вовсе. Как будто бы единственная реализуемая комбинация результатов возникла уже в момент t1. Как будто бы мы имели дело не с квантовой, а классической системой частиц.
Вот вам аналогия для прояснения седьмого постулата. Предположим, перед вами ветвистое дерево. Вы случайно выбираете одну веточку и дергаете за неё. Но тонкая ветка сидит прочно! Рывок передаётся более толстой "материнской" ветке, затем ещё более толстой и так до самого ствола. У ствола толстая ветка обламывается, и в итоге у вас в руках не одна веточка, а целый куст. Теперь просто сопоставим это с нашим опытом. Маленькие «веточки» дерева виртуальной реальности - это группы автономных виртуальных вариантов |+L〉, |-L〉, |+R〉, |- R〉. Толстые ветки - это группы виртуальных комбинаций |+L;+R〉, |+L;-R〉, |-L;+R〉, |-L;-R〉. На рисунках 15.2 я попытался изобразить всю эту «ботанику» в виде временных диаграмм. Вот на рисунке 15.2-а картина квантовой реальности перед первым измерением.

Нереализуемые группы обозначены пунктирными линиями. Реализуемые - штриховыми линиями.
На рисунке 15.2-б показан момент первого измерения - в момент t2 мы «дёргаем за веточку»,
тянем её из виртуальной реальности в классическую реальность, и видим, что это веточка 〈+L〉.

Но веточка |+L〉 в нашем эксперименте «намертво» запутана с веточкой |-R〉, вместе они образуют толстую ветку |+L;-R〉. Стало быть, наше измерение выдирает из квантовой реальности всю толстую ветку, которая «растёт» от момента времени t1. Это и есть «работа» седьмого постулата: измеряем мы в момент t2, но реализация варианта, ставшего результатом, происходит в прошлом, в момент t1. Рисунок 15.2-в иллюстрирует состояние системы после t2. Бывшая (до первого измерения) виртуальная ветка |+L;-R〉 показана сплошной линией, потому что теперь (после первого измерения) она стала бывшим классическим, то есть, единственно возможным вариантом. А если этот теперь классический вариант реализовался в тот момент, когда образовалась пара частиц, то и результат второго измерения 〈-R〉 теперь задним числом предопределён.

Как видите, такой механизм вполне объясняет квантовую корреляцию и при этом никакого канала нелокальной «суперсвязи» между частицами не требует.
Зато седьмой постулат требует другого странного явления, согласиться с которым "здравому смыслу" очень трудно. Ведь здесь, как ни крути, происходит обратный скачок во времени от момента измерения к моменту развилки вариантов и изменение прошлого. Но, друзья мои, вы ведь уже согласились (надеюсь) с существованием ненаблюдаемой квантовой реальности, битком набитой виртуальными вариантами будущего. Так сделайте следующий шаг и согласитесь с тем, что в квантовой реальности возможен также виртуальный отскок во времени. А "здравому смыслу" передайте, чтобы он не беспокоился: ни к каким временным парадоксам в классической реальности такие возвраты в прошлое не приводит. Ведь эти возвраты сугубо виртуальны, и использовать их для реальных путешествий во времени никак не получится. Зато, зная о их существовании, легко объяснить механизм квантовой нелокальности (надеюсь, мне это удалось), эксперименты с отложенным выбором и квантовую телепортацию (эти объяснения ещё впереди).
В защиту справедливости седьмого постулата, расскажу ещё вот что. Здесь уже не раз виртуальные варианты квантовой реальности сопоставлялись с мыслями в голове (вспомните притчу про буриданова осла в пятой части). Можно это сделать и сейчас: мысленно, то есть - виртуально, мы легко путешествуем в прошлое. Мы это делаем всякий раз, когда что-нибудь вспоминаем. Что, хотите возразить, что такие мысленные скачки не меняют, мол, прошлое? Да как сказать! Представьте себе: вы проснулись утром, позавтракали, пошли на работу. Всё как всегда, обычное утро, через неделю-другую оно потерялось бы в прошлом среди таких же обыденных утр (или утер?). Но этим же днём с вами вдруг случилось какое-то очень волнующее событие. Клад нашли, например, или влюбились с первого взгляда. И сразу же это утро перестанет быть обычным. Все сегодняшние утренние мелочи теперь, задним числом, обретут для вас значение предзнаменований и навсегда врежутся в память. Почему же обычное, уже прошедшее утро стало вдруг особенным? Потому что вы под впечатлением события совершили виртуальный мысленный возврат во времени и задним числом наполнили утро этого дня особым смыслом.
Как, ваш "здравый смысл" до сих протестует? Тогда приведу самый, как мне кажется, веский довод.
Проведём следующий мысленный эксперимент. Одну частицу скоррелированной пары отдаём Алисе, вторую отдаём Бобу. Алиса и Боб сверяют часы и, каждый со своей частицей, разъёзжаются на достаточно далёкое расстояние. Допустим, Алиса едет на Северный полюс, а Боб - на Южный.
Одновременно, в оговоренный момент времени, Алиса и Боб измеряют спины своих частиц. Ну как одновременно? Сколь бы не были точны их часы, на практике какое-то расхождение, пусть на миллионную, пусть на триллионную долю секунды, будет. И всё равно получится, что кто-то из них измерит чуть раньше. Пусть первой будет Алиса.
Мы помним, что до измерения обе частицы ЭПР-пары находятся в неопределённом состоянии. Но как только Алиса проведёт измерение, её частица переходит в какое-то определённое состояние. Но не только, частица Боба тоже "автоматом" определяется. Казалось бы, вполне резонно думать, что результат Алисы является причиной, а результат Боба - следствием.
Однако не будем забывать о "фокусах" специальной теории относительности, где понятия "раньше" и "позже" вовсе не абсолютны. Если события "А" и "Б" происходят в разных точках пространства, то в одной системе отсчёта события "А" и "Б" могут произойти одновременно. В другой "А" происходит раньше "В". В третьей, наоборот, раньше происходит "В".
Так вот, мы условились, что в системе отсчёта, относительно которой оба экспериментатора неподвижны, Алиса измеряет на мгновение раньше Боба. Но, согласно теории относительности, существуют и такие системы отсчёта, где первым измеряет Боб. И мы вынуждены считать, что в этих системах отсчёта следствие (результат Боба) происходит раньше причины (результат Алисы). А это тоже отскок по времени, как не крути.
Вот, теперь хоть отвергаем седьмой постулат, хоть принимаем. Так или иначе, мы вынуждены допускать возможность отскока в прошлое. Но отскок отскоку рознь! Согласно той же теории относительности, если событие "А" является причиной, а событие "В" - следствием, тогда "А" происходит раньше в любой системе отсчёта. Теперь давайте посмотрим, как у нас с этим правилом.
В первом случае (принимаем постулат) отскок происходит в квантовой реальности. Не важно при этом, кто стал инициатором отскока, Алиса или Боб. До измерения оба они, и любой внешний наблюдатель, существуют в реальности, где спины частиц не определены. А после первого измерения эта реальность просто стирается и подменяется на такую, в которой спины определены. Причём, стирается "задним числом". В этой новой реальности ни результат Алисы, ни результат Боба уже не являются причиной. Оба результата - следствие прошлого события, а именно рождения квантово запутанной пары частиц. Таким образом, в обновившейся реальности ни для какого из наблюбателей не существует абсурдной ситуации "следствие опержает причину".
Во втором случае (отвергаем постулат) никакого стирания несостоявшихся виртуальных реальностей не происходит, следствие, получается, предшествует причине в самом что ни на есть классическом смысле. Тогда мы должны признать, что теория относительности в какой-то части "врёт". Лично мне такой подход не кажется состоятельным, так что предлагаю всё же принять седьмой постулат.
Ура! Все восемь постулатов квантовой философии (напомню, что отсчёт начался с нуля) теперь озвучены и разобраны. В следующей части мы рассмотрим некоторые вопросы, которые пока что оставались "за кадром" ликбеза. И заодно немного расширим математический аппарат, с которым мы начали знакомиться в части 12. Этот "аппарат" нам очень понадобится дальше, когда мы будем осваивать принцип действия квантового компьютера.
Продолжение