Квантовый ликбез - 10. Пятый постулат.
Предыдущие посты
Тут мы поговорим о том, как квантовое состояние меняется во времени. А также потолкуем о детерминизме, классическом и квантовом.
Если рассматривать квантовую и классическую реальности в их совокупности, то первую можно представлять себе как бесконечный набор будущих возможностей, а вторую - как свершившийся факт реализации одной из этих возможностей. Сама по себе такая картина мира не так уж и необычна, примерно так же мы представляем себе прошлое, будущее и настоящее. Прошлое - одно, оно уже свершилось, и изменить его нельзя. Будущее - это огромный «пучок» возможностей. А настоящее - это точечная граница между единственной линией событий прошлого и пучком возможностей будущего. Схематично это можно показать так.
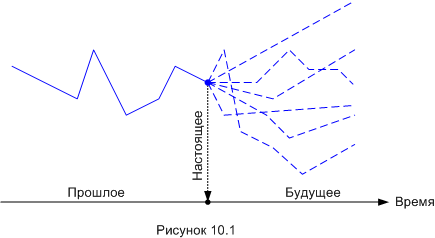
Сплошной синей линией показан единственный состоявшийся путь объекта в прошлом, а прерывистыми линиями - возможные пути в будущем. Слово «путь» тут не надо понимать буквально. Да, так могла бы выглядеть, например, «траектория» бредущего пьяницы - это в прямом смысле «путь». Но так же мог бы выглядеть график продаж коммерческой фирмы. Или средняя температура по больнице. Вообще любой параметр любой системы.
Конечно, когда мы говорим о физических объектах и их параметрах (я сейчас имею в виду классическую физику), то мы полагаем, что будущий путь тоже единственный, как и прошлый. То есть, что будущее состояние объекта полностью и однозначно предопределено начальными условиями и законами физики - в этом заключается суть классического детерминизма. С точки зрения строго детерминизма схема должна выглядеть как-то так
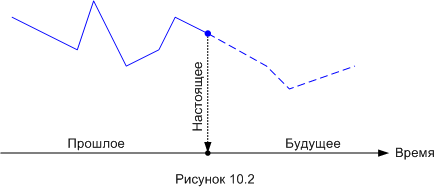
Вот, слева от точки настоящего единственное состоявшееся прошлое. Справа - ещё не состоявшееся, но тоже единственное будущее. Точнее, единственно возможное, предопределённое будущее.
Однако, в «обычной» жизни, вне строгих наук мы так «механистично» не мыслим и не считаем, что будущее предопределено. Если мы, допустим, выбираем, чем заняться в выходные - организовать шашлык на природе, сводить детей в зоопарк, поваляться на диване у телевизора или просто выспаться - то все эти и прочие варианты представляются нам возможными. И мы не думаем, что какой-то из них предопределён. Хотя бы уже потому, что нам комфортнее жить с ощущением свободы воли, чем считать себя автоматами с программой. Так что картина типа той, что показана на рисунке 10.1 - единственное прошлое и многовариантное будущее - более соответствует нашим «житейским» представлениям о мире.
Замечаете противоречие? Когда мы рассматриваем законы физики (классической), мы предпочитаем придерживаться концепции детерминизма. А когда мы говорим о сложных системах, например, о себе, любимых, или о мире вообще, тогда предопределённость мы интуитивно отвергаем. Так вот, квантовая физика это противоречие если не устраняет совсем, то, по крайней мере, значительно ослабляет. Она утверждает, что будущее простых физических объектов тоже многовариантно. Таким образом, квантовая физика на самом деле нам должна быть «идейно» ближе, чем физика классическая. Ведь она даёт некоторую «свободу воли» даже самым простейшим объектам. Это я к тому говорю, чтобы вам легче было проникнуться квантовой мультивариантностью.
Однако тем, кому жаль расставаться с детерминизмом, я могу «капнуть бальзамчика»: в квантовой реальности действует такая же строгая предопределённость, как и в классической. Чуть забегая вперёд, скажу, что «разрыв» предопределённости осуществляется только в момент квантового скачка, то есть, когда один из множества виртуальных вариантов будущего превращается в результат. А пока давайте разберёмся с предопределённостью в квантовой реальности.
Начнём, как у нас повелось, с рассмотрения классических ситуаций, и скажем совершенно банальную вещь: классическое физическое состояние меняется во времени. Этот процесс предопределён, а значит, можно смело утверждать, что все будущие состояния физической системы «записаны» в её текущем состоянии. На всякий случай оговорка: речь идёт о замкнутой системе. В смысле, такой системы, которая не испытывает никаких внешних воздействий. Для примера возьмём снова нашу любимую частицу, свободно движущуюся в пустом пространстве. Опять для упрощения будем рассматривать движение только вдоль координатной оси X. Мгновенное состояние частицы описывается двумя физическими величинами: координатой X и скоростью Vx. Но эти две величины определяют не только текущее, но и будущее состояние системы на любой момент времени. Аналогично и для любой, сколь угодно сложной классической (замкнутой) системы: текущее состояние полностью предопределяет процесс изменения состояния системы во времени (дальше будем говорить просто «процесс»), а значит предопределяет и все будущие состояния системы. Именно это обстоятельство позволяет нам говорить о том, что состояние системы на настоящий момент времени - это вариант её будущего. В классической физике этот вариант, разумеется, единственный (смотрим опять на рисунок 10.2).
А как меняется квантовое состояние? К объяснению этого возможны два подхода.
Первый подход весьма поверхностный, но зато наглядный. Во второй части уже говорилось, что можно понимать квантовые варианты как классические состояния неких виртуальных частиц. Каждая виртуальная частица обладает классическим набором параметров: координатами, скоростями, импульсами и так далее. При таком подходе мы можем рассматривать процесс изменения квантового состояния как совокупность виртуальных классических процессов, для каждой виртуальной частицы - свой. В классической реальности мы рассматриваем мгновенное состояние частицы как одно значение координаты, допустим, X. А полёт частицы - как процесс изменения этого значения во времени. Но в квантовой реальности (если бы мы могли её непосредственно наблюдать) всё выглядело бы как полёт целого роя виртуальных частиц. Каждая виртуальная частица движется "классически", в полном соответствии с первым законом Ньютона. Со своим (одним!) значением скорости, которое постоянно. И со своим (тоже одним!) значением координаты в каждый момент времени. В таком понимании изменение во времени квантового состояния - это, по сути, изменение состояния этого виртуального "роя".
Маленький числовой пример для иллюстрации идеи. Пусть наш "рой" состоит всего из двух виртуальных частиц: "A" и "B". В квантовой реальности так не бывает, конечно, но для понимания принципа двух частиц достаточно. Пусть в момент времени t0 виртуальные частицы имеют следующие значения координат и скоростей:
Частица A: XA0 = 0 (м); VxA0 = 100 (м/с)
Частица B: XB0 = 10 (м); VxB0 = 50 (м/с)
Этот набор значений, по сути дела, является описанием квантового состояния на момент времени t0. Неполным описанием, конечно, потому что мы тут проигнорировали направление квантовых векторов. Именно в этом и кроется "поверхностность" первого подхода. Ладно, это "упущение" мы чуть погодя исправим. А пока легко видеть, как это состояние меняется во времени. Например, через одну секунду (пусть это будет момент времени t1) оно будет выглядеть так:
XA0 = 100 (м)
XB0 = 60 (м)
Скорости виртуальных частиц, разумеется, останутся теми же, что и были в момент t0.
Надеюсь, теперь вы легко распространите этот куцый пример на бесконечное множество виртуальных частиц. Кстати говоря, такой подход к квантовым процессам мы уже применяли, когда рассматривали некоторые опыты в третьей части. Мы говорили, что одиночный фотон летит в квантовой реальности по разным виртуальным траекториям одновременно. Это, согласитесь, равносильно утверждению о том, что фотон в квантовой реальности представляет собой рой виртуальных фотонов, каждый из которых летит по своей собственной траектории.
Теперь используем второй подход. Основная его "фишка" заключается в том, что в квантовой реальности ничего никуда не летит. Для любого квантового объекта в каждый момент времени есть только бесконечный набор виртуальных вариантов, или, что то же самое, виртуальных классических состояний. Каждый виртуальный вариант имеет фиксированный и неизменный во времени набор классических параметров. Например, и в момент времени t0, и в момент t1, и вообще в любой момент в бесконечном наборе имеется виртуальный вариант со значениями координаты и скорости:
XA0 = 0 (м); VxA0 = 100 (м/с),
равно как имеется и любой другой вариант.
Но квантовый вектор каждого виртуального варианта с течением времени меняется. Точнее - меняется его направление. Формулируем:
Постулат 5:
Квантовый вектор виртуального варианта равномерно вращается. Частота вращения пропорциональна «энергетике» варианта.
Да, прошу не воспринимать слово "вращаются" слишком буквально. В очередной раз подчеркну, что вращение квантового вектора, направление квантового вектора, да и вообще сам квантовый вектор - это всего лишь условности, модели, позволяющие представить себе происходящее более наглядно. На самом деле речь идёт о существовании у виртуальных вариантов некоего физического параметра, который можно охарактеризовать двумя действительными числами или, что удобнее, одним комплексным числом. И эти два числа меняются во времени согласованно, точно так же, как согласованно меняются значения координат X и Y конца вектора, вращающегося на координатной плоскости вокруг собственного начала. То есть, когда мы говорим о том, что квантовый вектор вращается, мы имеем в виду, что эти числа периодически и согласованно меняются "по синусоиде". Аналогично тому, как периодически и согласованно меняются значения напряжения и силы тока в питающей ваш компьютер электрической розетке. Но вращающийся вектор всё же более наглядная модель, чем колонка тригонометрических формул, поэтому ими, векторами, мы и будем оперировать дальше.
Теперь несколько слов о частоте вращения и «энергетике». В классической физике, как вы, конечно, знаете, с любым физическим состоянием связано определённое значение энергии. Например, кинетическая энергия свободно движущегося тела зависит от скорости. Или, скажем, потенциальная энергия взаимодействующих тел зависит от их взаимных координат. Аналогичная картина и в квантовой реальности: с каждым виртуальным вариантом состояния связано определённое виртуальное значение энергии. И чем эта виртуальная энергия больше - тем быстрее вращается квантовый вектор.
Теперь, вооружившись пятым постулатом, давайте разберёмся, как "на самом деле" движутся частицы в квантовой реальности. Пример такого "движения" показан на рисунке 10.3.
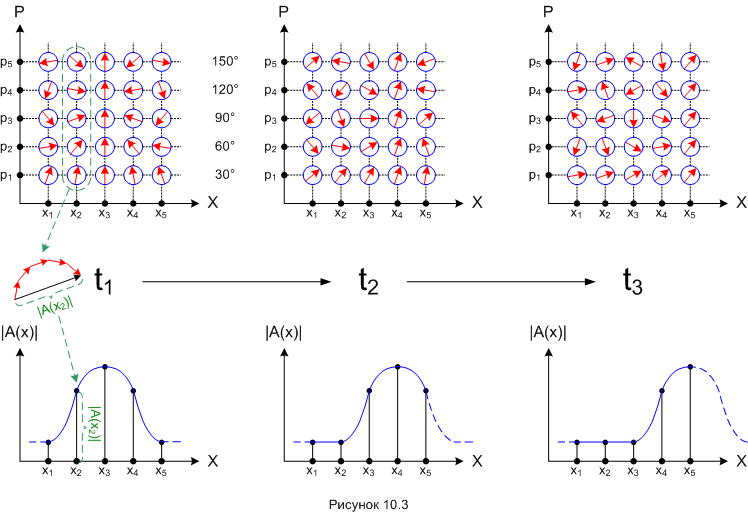
Верхний ряд рисунков показывает квантовые состояния некой движущейся частицы в последовательные моменты времени t1, t2, t3. Похожие картинки мы рисовали в предыдущей части (рисунок 9.4). Каждое из 25-ти виртуальных состояний (показаны кружочками) "привязано" к определённому значению координаты и импульса. И у каждого - своё направление квантового вектора. Если честно, направления квантовых векторов тут выбраны "с потолка", ни к какой реальной физической ситуации мои картинки не привязаны, однако, надеюсь, это не помешает вам понять сам принцип.
Нижний ряд рисунков - значения модулей (длин векторов) амплитуд вероятности для разных значений координаты в те же моменты времени t1, t2, t3. Слева в центре там ещё схема, поясняющая, как квантовые вектора одной группы вариантов складываются в групповой вектор амплитуды вероятности. Сложение векторов показано для группы x2 в момент времени t1, для прочих групп и моментов времени это делается аналогично. Мы взяли всего по пять значений. Если бы мы построили эти графики более точно, то получились бы гладкие кривые, похожие на волну, они тоже показаны на нижних рисунках.
При такой ориентации квантовых векторов максимум длины амплитуды вероятности в момент времени t1 приходится на значение координаты x3. За один такт времени, от момента t1 к моменту t2, квантовые вектора всех вариантов поворачиваются в своём условном пространстве на некоторый угол. Этот угол, как сказано выше, зависит от виртуальной энергии варианта, в данном случае - от значения виртуального импульса частицы. Для всех вариантов в одном горизонтальном ряду значение импульса одинаково, значит, их вектора поворачиваются на одинаковый угол. Например, для нижнего ряда со значением импульса p1 это угол равен 30° (по часовой стрелке).
Но вектора следующих горизонтальных рядов поворачиваются за то же время на больший угол, потому что значение импульса от ряда к ряду растёт. Для p2 - поворот на 60°, для p3 - на 90° и так далее. Все эти повороты приводят к тому, что в момент времени t2 максимум длины амплитуды вероятности приходится на координату x4. На следующем такте, к моменту времени t3, максимум приходится уже на координату x5. Короче, с течением времени этот «горб» амплитуды вероятности перемещается в пространстве вдоль оси X. Этот процесс я попытался изобразить на рисунке 10.4.
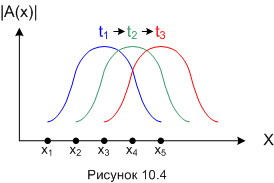
Как видите, говорить о движении частицы в квантовой реальности вообще некорректно. Зато корректно говорить о вращении квантовых векторов виртуальных состояний, следствием которого является "движение" максимума вероятности обнаружить частицу в той или иной точке пространства.
Если эти идеи понятны, то должно быть понятно также, "откуда ноги растут" у корпускулярно-волнового дуализма и у волн де Бройля. Напомню, де Бройль установил, что любая частица является так же волной, и частота этой волны прямо пропорциональна массе частицы (у нас в пятом постулате частота пропорциональна энергии варианта, а энергия и масса, как вы знаете, это практически одно и то же). На самом деле в наблюдаемой, классической реальности частица - это только частица, она всегда наблюдается как точечный объект. Но до момента наблюдения, пока частица пребывает в квантовой реальности, она не находится "нигде", и существует только как совокупность виртуальных вариантов обнаружить её в том или ином месте. Вращение квантовых векторов виртуальных вариантов в совокупности с суперпозицией этих векторов как раз и обеспечивает волновую картину: в одном месте вероятность обнаружения может быть большей, в другом месте - меньшей, в прочих местах - вообще бесконечно близкой к нулю. И вот эта картина распределения вероятностей может со временем изменяться, как изменяется поверхность водоёма при волнении. Максимумы и минимумы амплитуды вероятностей распространяются в пространстве примерно также, как распространяются гребни и впадины обычных волн. И также могут интерферировать между собой, взаимно усиливая, или, наоборот, ослабляя друг друга. Вот такой вот "дуализм".
Мы тут говорили сейчас о движении, то есть, рассматривали, как изменяется квантовое состояние в координатном представлении. Аналогичные рассуждения верны для любого другого представления. Например, в импульсном представлении мы говорили бы о том, как изменяется во времени вероятность измерить то или иное значение импульса. То же самое касается любого другого представления квантового состояния. Общий принцип сохраняется: квантовые вектора всех виртуальных вариантов "крутятся", и частота их вращения тем больше, чем больше виртуальная энергия варианта.
В рассмотренном примере с движением частицы вероятность того или иного результата измерения (значения координаты) меняется во времени. Однако, бывают и стационарные состояния. Для стационарных состояний пятый постулат тоже работает: квантовые вектора виртуальных вариантов крутятся. Групповые вектора - амплитуды вероятности - крутятся тоже. Но соотношения между амплитудами вероятности различных групп при этом не изменяются, а значит, не изменяются и вероятности возможных результатов измерений. Секрет такой "стабильности" прост: в стационарном состоянии квантовые вектора всех виртуальных вариантов во всех группах вращаются согласовано, с одинаковой частотой.
Для пояснения разницы между нестационарным и стационарным квантовым состоянием можно привести ещё такую аналогию. Представьте себе сначала команду бегунов на стадионе. В момент старта команда представляет собой ровную шеренгу, но после старта кто-то бежит быстрее, кто-то медленнее, и команда со временем "размазывается" по дистанции в довольно бесформенное пятно. Это аналог нестационарного состояния. Теперь представьте шеренгу марширующих в ногу военных: все они движутся с одной скоростью, и строй сохраняется. Это аналог стационарного состояния.
В дальнейшем, когда речь пойдёт о квантовой запутанности, квантовой телепортации и квантовых компьютерах, мы будем "работать" именно со стационарными состояниями.
В завершение этой части я хочу ещё раз подчеркнуть: все эти процессы, происходящие "внутри" квантовой реальности, детерминированы столь же строго, как и "классические" процессы. Классическое физическое состояние меняется в полном согласии с классическими же законами, законами Ньютона, в частности. Эволюция квантового состояния тоже подчиняется строгому физическому закону, который выражется математически как уравнение Шредингера. Замечу попутно, что "традиционные" уравнения квантовой механики "игнорируют" существование в квантовой реальности отдельных виртуальных вариантов с их индивидуальными квантовыми векторами. Уравнения «работают» только с групповыми квантовыми векторами - амплитудами вероятности. Разумеется, на качество и полноту квантовых расчётов это никак не влияет, как не влияет, например, на "качество" закона Бойля-Мариотта игнорирование того факта, что газ состоит из отдельных микрочастиц. Но наша задача - не овладение математическими тонкостями квантовых уравнений, а понимание их физического смысла. Поэтому мы идею виртуальных вариантов игнорировать не будем.
А о том, когда, как и почему происходит «разрыв» предопределённости, мы поговорим в следующей серии.
Продолжение следует.
Тут мы поговорим о том, как квантовое состояние меняется во времени. А также потолкуем о детерминизме, классическом и квантовом.
Если рассматривать квантовую и классическую реальности в их совокупности, то первую можно представлять себе как бесконечный набор будущих возможностей, а вторую - как свершившийся факт реализации одной из этих возможностей. Сама по себе такая картина мира не так уж и необычна, примерно так же мы представляем себе прошлое, будущее и настоящее. Прошлое - одно, оно уже свершилось, и изменить его нельзя. Будущее - это огромный «пучок» возможностей. А настоящее - это точечная граница между единственной линией событий прошлого и пучком возможностей будущего. Схематично это можно показать так.

Сплошной синей линией показан единственный состоявшийся путь объекта в прошлом, а прерывистыми линиями - возможные пути в будущем. Слово «путь» тут не надо понимать буквально. Да, так могла бы выглядеть, например, «траектория» бредущего пьяницы - это в прямом смысле «путь». Но так же мог бы выглядеть график продаж коммерческой фирмы. Или средняя температура по больнице. Вообще любой параметр любой системы.
Конечно, когда мы говорим о физических объектах и их параметрах (я сейчас имею в виду классическую физику), то мы полагаем, что будущий путь тоже единственный, как и прошлый. То есть, что будущее состояние объекта полностью и однозначно предопределено начальными условиями и законами физики - в этом заключается суть классического детерминизма. С точки зрения строго детерминизма схема должна выглядеть как-то так

Вот, слева от точки настоящего единственное состоявшееся прошлое. Справа - ещё не состоявшееся, но тоже единственное будущее. Точнее, единственно возможное, предопределённое будущее.
Однако, в «обычной» жизни, вне строгих наук мы так «механистично» не мыслим и не считаем, что будущее предопределено. Если мы, допустим, выбираем, чем заняться в выходные - организовать шашлык на природе, сводить детей в зоопарк, поваляться на диване у телевизора или просто выспаться - то все эти и прочие варианты представляются нам возможными. И мы не думаем, что какой-то из них предопределён. Хотя бы уже потому, что нам комфортнее жить с ощущением свободы воли, чем считать себя автоматами с программой. Так что картина типа той, что показана на рисунке 10.1 - единственное прошлое и многовариантное будущее - более соответствует нашим «житейским» представлениям о мире.
Замечаете противоречие? Когда мы рассматриваем законы физики (классической), мы предпочитаем придерживаться концепции детерминизма. А когда мы говорим о сложных системах, например, о себе, любимых, или о мире вообще, тогда предопределённость мы интуитивно отвергаем. Так вот, квантовая физика это противоречие если не устраняет совсем, то, по крайней мере, значительно ослабляет. Она утверждает, что будущее простых физических объектов тоже многовариантно. Таким образом, квантовая физика на самом деле нам должна быть «идейно» ближе, чем физика классическая. Ведь она даёт некоторую «свободу воли» даже самым простейшим объектам. Это я к тому говорю, чтобы вам легче было проникнуться квантовой мультивариантностью.
Однако тем, кому жаль расставаться с детерминизмом, я могу «капнуть бальзамчика»: в квантовой реальности действует такая же строгая предопределённость, как и в классической. Чуть забегая вперёд, скажу, что «разрыв» предопределённости осуществляется только в момент квантового скачка, то есть, когда один из множества виртуальных вариантов будущего превращается в результат. А пока давайте разберёмся с предопределённостью в квантовой реальности.
Начнём, как у нас повелось, с рассмотрения классических ситуаций, и скажем совершенно банальную вещь: классическое физическое состояние меняется во времени. Этот процесс предопределён, а значит, можно смело утверждать, что все будущие состояния физической системы «записаны» в её текущем состоянии. На всякий случай оговорка: речь идёт о замкнутой системе. В смысле, такой системы, которая не испытывает никаких внешних воздействий. Для примера возьмём снова нашу любимую частицу, свободно движущуюся в пустом пространстве. Опять для упрощения будем рассматривать движение только вдоль координатной оси X. Мгновенное состояние частицы описывается двумя физическими величинами: координатой X и скоростью Vx. Но эти две величины определяют не только текущее, но и будущее состояние системы на любой момент времени. Аналогично и для любой, сколь угодно сложной классической (замкнутой) системы: текущее состояние полностью предопределяет процесс изменения состояния системы во времени (дальше будем говорить просто «процесс»), а значит предопределяет и все будущие состояния системы. Именно это обстоятельство позволяет нам говорить о том, что состояние системы на настоящий момент времени - это вариант её будущего. В классической физике этот вариант, разумеется, единственный (смотрим опять на рисунок 10.2).
А как меняется квантовое состояние? К объяснению этого возможны два подхода.
Первый подход весьма поверхностный, но зато наглядный. Во второй части уже говорилось, что можно понимать квантовые варианты как классические состояния неких виртуальных частиц. Каждая виртуальная частица обладает классическим набором параметров: координатами, скоростями, импульсами и так далее. При таком подходе мы можем рассматривать процесс изменения квантового состояния как совокупность виртуальных классических процессов, для каждой виртуальной частицы - свой. В классической реальности мы рассматриваем мгновенное состояние частицы как одно значение координаты, допустим, X. А полёт частицы - как процесс изменения этого значения во времени. Но в квантовой реальности (если бы мы могли её непосредственно наблюдать) всё выглядело бы как полёт целого роя виртуальных частиц. Каждая виртуальная частица движется "классически", в полном соответствии с первым законом Ньютона. Со своим (одним!) значением скорости, которое постоянно. И со своим (тоже одним!) значением координаты в каждый момент времени. В таком понимании изменение во времени квантового состояния - это, по сути, изменение состояния этого виртуального "роя".
Маленький числовой пример для иллюстрации идеи. Пусть наш "рой" состоит всего из двух виртуальных частиц: "A" и "B". В квантовой реальности так не бывает, конечно, но для понимания принципа двух частиц достаточно. Пусть в момент времени t0 виртуальные частицы имеют следующие значения координат и скоростей:
Частица A: XA0 = 0 (м); VxA0 = 100 (м/с)
Частица B: XB0 = 10 (м); VxB0 = 50 (м/с)
Этот набор значений, по сути дела, является описанием квантового состояния на момент времени t0. Неполным описанием, конечно, потому что мы тут проигнорировали направление квантовых векторов. Именно в этом и кроется "поверхностность" первого подхода. Ладно, это "упущение" мы чуть погодя исправим. А пока легко видеть, как это состояние меняется во времени. Например, через одну секунду (пусть это будет момент времени t1) оно будет выглядеть так:
XA0 = 100 (м)
XB0 = 60 (м)
Скорости виртуальных частиц, разумеется, останутся теми же, что и были в момент t0.
Надеюсь, теперь вы легко распространите этот куцый пример на бесконечное множество виртуальных частиц. Кстати говоря, такой подход к квантовым процессам мы уже применяли, когда рассматривали некоторые опыты в третьей части. Мы говорили, что одиночный фотон летит в квантовой реальности по разным виртуальным траекториям одновременно. Это, согласитесь, равносильно утверждению о том, что фотон в квантовой реальности представляет собой рой виртуальных фотонов, каждый из которых летит по своей собственной траектории.
Теперь используем второй подход. Основная его "фишка" заключается в том, что в квантовой реальности ничего никуда не летит. Для любого квантового объекта в каждый момент времени есть только бесконечный набор виртуальных вариантов, или, что то же самое, виртуальных классических состояний. Каждый виртуальный вариант имеет фиксированный и неизменный во времени набор классических параметров. Например, и в момент времени t0, и в момент t1, и вообще в любой момент в бесконечном наборе имеется виртуальный вариант со значениями координаты и скорости:
XA0 = 0 (м); VxA0 = 100 (м/с),
равно как имеется и любой другой вариант.
Но квантовый вектор каждого виртуального варианта с течением времени меняется. Точнее - меняется его направление. Формулируем:
Постулат 5:
Квантовый вектор виртуального варианта равномерно вращается. Частота вращения пропорциональна «энергетике» варианта.
Да, прошу не воспринимать слово "вращаются" слишком буквально. В очередной раз подчеркну, что вращение квантового вектора, направление квантового вектора, да и вообще сам квантовый вектор - это всего лишь условности, модели, позволяющие представить себе происходящее более наглядно. На самом деле речь идёт о существовании у виртуальных вариантов некоего физического параметра, который можно охарактеризовать двумя действительными числами или, что удобнее, одним комплексным числом. И эти два числа меняются во времени согласованно, точно так же, как согласованно меняются значения координат X и Y конца вектора, вращающегося на координатной плоскости вокруг собственного начала. То есть, когда мы говорим о том, что квантовый вектор вращается, мы имеем в виду, что эти числа периодически и согласованно меняются "по синусоиде". Аналогично тому, как периодически и согласованно меняются значения напряжения и силы тока в питающей ваш компьютер электрической розетке. Но вращающийся вектор всё же более наглядная модель, чем колонка тригонометрических формул, поэтому ими, векторами, мы и будем оперировать дальше.
Теперь несколько слов о частоте вращения и «энергетике». В классической физике, как вы, конечно, знаете, с любым физическим состоянием связано определённое значение энергии. Например, кинетическая энергия свободно движущегося тела зависит от скорости. Или, скажем, потенциальная энергия взаимодействующих тел зависит от их взаимных координат. Аналогичная картина и в квантовой реальности: с каждым виртуальным вариантом состояния связано определённое виртуальное значение энергии. И чем эта виртуальная энергия больше - тем быстрее вращается квантовый вектор.
Теперь, вооружившись пятым постулатом, давайте разберёмся, как "на самом деле" движутся частицы в квантовой реальности. Пример такого "движения" показан на рисунке 10.3.

Верхний ряд рисунков показывает квантовые состояния некой движущейся частицы в последовательные моменты времени t1, t2, t3. Похожие картинки мы рисовали в предыдущей части (рисунок 9.4). Каждое из 25-ти виртуальных состояний (показаны кружочками) "привязано" к определённому значению координаты и импульса. И у каждого - своё направление квантового вектора. Если честно, направления квантовых векторов тут выбраны "с потолка", ни к какой реальной физической ситуации мои картинки не привязаны, однако, надеюсь, это не помешает вам понять сам принцип.
Нижний ряд рисунков - значения модулей (длин векторов) амплитуд вероятности для разных значений координаты в те же моменты времени t1, t2, t3. Слева в центре там ещё схема, поясняющая, как квантовые вектора одной группы вариантов складываются в групповой вектор амплитуды вероятности. Сложение векторов показано для группы x2 в момент времени t1, для прочих групп и моментов времени это делается аналогично. Мы взяли всего по пять значений. Если бы мы построили эти графики более точно, то получились бы гладкие кривые, похожие на волну, они тоже показаны на нижних рисунках.
При такой ориентации квантовых векторов максимум длины амплитуды вероятности в момент времени t1 приходится на значение координаты x3. За один такт времени, от момента t1 к моменту t2, квантовые вектора всех вариантов поворачиваются в своём условном пространстве на некоторый угол. Этот угол, как сказано выше, зависит от виртуальной энергии варианта, в данном случае - от значения виртуального импульса частицы. Для всех вариантов в одном горизонтальном ряду значение импульса одинаково, значит, их вектора поворачиваются на одинаковый угол. Например, для нижнего ряда со значением импульса p1 это угол равен 30° (по часовой стрелке).
Но вектора следующих горизонтальных рядов поворачиваются за то же время на больший угол, потому что значение импульса от ряда к ряду растёт. Для p2 - поворот на 60°, для p3 - на 90° и так далее. Все эти повороты приводят к тому, что в момент времени t2 максимум длины амплитуды вероятности приходится на координату x4. На следующем такте, к моменту времени t3, максимум приходится уже на координату x5. Короче, с течением времени этот «горб» амплитуды вероятности перемещается в пространстве вдоль оси X. Этот процесс я попытался изобразить на рисунке 10.4.

Как видите, говорить о движении частицы в квантовой реальности вообще некорректно. Зато корректно говорить о вращении квантовых векторов виртуальных состояний, следствием которого является "движение" максимума вероятности обнаружить частицу в той или иной точке пространства.
Если эти идеи понятны, то должно быть понятно также, "откуда ноги растут" у корпускулярно-волнового дуализма и у волн де Бройля. Напомню, де Бройль установил, что любая частица является так же волной, и частота этой волны прямо пропорциональна массе частицы (у нас в пятом постулате частота пропорциональна энергии варианта, а энергия и масса, как вы знаете, это практически одно и то же). На самом деле в наблюдаемой, классической реальности частица - это только частица, она всегда наблюдается как точечный объект. Но до момента наблюдения, пока частица пребывает в квантовой реальности, она не находится "нигде", и существует только как совокупность виртуальных вариантов обнаружить её в том или ином месте. Вращение квантовых векторов виртуальных вариантов в совокупности с суперпозицией этих векторов как раз и обеспечивает волновую картину: в одном месте вероятность обнаружения может быть большей, в другом месте - меньшей, в прочих местах - вообще бесконечно близкой к нулю. И вот эта картина распределения вероятностей может со временем изменяться, как изменяется поверхность водоёма при волнении. Максимумы и минимумы амплитуды вероятностей распространяются в пространстве примерно также, как распространяются гребни и впадины обычных волн. И также могут интерферировать между собой, взаимно усиливая, или, наоборот, ослабляя друг друга. Вот такой вот "дуализм".
Мы тут говорили сейчас о движении, то есть, рассматривали, как изменяется квантовое состояние в координатном представлении. Аналогичные рассуждения верны для любого другого представления. Например, в импульсном представлении мы говорили бы о том, как изменяется во времени вероятность измерить то или иное значение импульса. То же самое касается любого другого представления квантового состояния. Общий принцип сохраняется: квантовые вектора всех виртуальных вариантов "крутятся", и частота их вращения тем больше, чем больше виртуальная энергия варианта.
В рассмотренном примере с движением частицы вероятность того или иного результата измерения (значения координаты) меняется во времени. Однако, бывают и стационарные состояния. Для стационарных состояний пятый постулат тоже работает: квантовые вектора виртуальных вариантов крутятся. Групповые вектора - амплитуды вероятности - крутятся тоже. Но соотношения между амплитудами вероятности различных групп при этом не изменяются, а значит, не изменяются и вероятности возможных результатов измерений. Секрет такой "стабильности" прост: в стационарном состоянии квантовые вектора всех виртуальных вариантов во всех группах вращаются согласовано, с одинаковой частотой.
Для пояснения разницы между нестационарным и стационарным квантовым состоянием можно привести ещё такую аналогию. Представьте себе сначала команду бегунов на стадионе. В момент старта команда представляет собой ровную шеренгу, но после старта кто-то бежит быстрее, кто-то медленнее, и команда со временем "размазывается" по дистанции в довольно бесформенное пятно. Это аналог нестационарного состояния. Теперь представьте шеренгу марширующих в ногу военных: все они движутся с одной скоростью, и строй сохраняется. Это аналог стационарного состояния.
В дальнейшем, когда речь пойдёт о квантовой запутанности, квантовой телепортации и квантовых компьютерах, мы будем "работать" именно со стационарными состояниями.
В завершение этой части я хочу ещё раз подчеркнуть: все эти процессы, происходящие "внутри" квантовой реальности, детерминированы столь же строго, как и "классические" процессы. Классическое физическое состояние меняется в полном согласии с классическими же законами, законами Ньютона, в частности. Эволюция квантового состояния тоже подчиняется строгому физическому закону, который выражется математически как уравнение Шредингера. Замечу попутно, что "традиционные" уравнения квантовой механики "игнорируют" существование в квантовой реальности отдельных виртуальных вариантов с их индивидуальными квантовыми векторами. Уравнения «работают» только с групповыми квантовыми векторами - амплитудами вероятности. Разумеется, на качество и полноту квантовых расчётов это никак не влияет, как не влияет, например, на "качество" закона Бойля-Мариотта игнорирование того факта, что газ состоит из отдельных микрочастиц. Но наша задача - не овладение математическими тонкостями квантовых уравнений, а понимание их физического смысла. Поэтому мы идею виртуальных вариантов игнорировать не будем.
А о том, когда, как и почему происходит «разрыв» предопределённости, мы поговорим в следующей серии.
Продолжение следует.