Правда и ложь о задаче коммивояжера
В этом году известные ("блестящие умы" они себя кличут) и не очень экономисты во всеуслышанье признавались не шмогла я, что их модели не позволили предсказать кризис, да и сейчас не очень-то ясно что делать и особенно неясно - как узнать что делать. Модели то те же 
.
В свете вышеизложенного lex-kravetski опять запалил дискуссию о планировании экономики и опять с тем же результатом - то есть все остались при своем мнении. "Убежденные" рыночники невзирая на всю шизовость аргументации настаивают, что задача оптимизации плана на миллионы товарных позиций требует ресурсов и времени на порядки больше, чем имеется во Вселенной. Часто в пример неподъемности ссылаются на задачу коммивояжера (ЗК), которой еще сам Гамильтон баловался. Антирыночники пытаются рассказать о надуманности такой аналогии, но на словах выходит не очень убедительно.
Коммивояжер должен по разу посетить несколько городов, надо найти такой порядок посещения, чтоб суммарный путь был наикратчайшим. Эта простая на первый взгляд задача аналитического решения вроде бы не имеет, а просто перебрать все комбинации затруднительно: при N городов число возможных путей (перестановок) 1*2*3*4*..*(N-1)*N = N!
20! = 2432902008176640000. Если один расчет в наносекунду, то перебор маршуртов через 20 городов займет 2.5 миллиарда секунд - лет 70. Ну а 30! = 265252859812191058636308480000000, в 100 триллионов раз больше. "И не сосчитаешь !"
Все же я решил пощупать страшную задачу руками.

Накидал скрипт, перебирающий все перестановки, поместил случайным образом "города" в квадрате 10x10 и запустил подсчет длины всех возможных путей. В моем варианте коммивояжер как бы выдвигался из точки (0, 0), проезжал через все N городов и возвращался на исходную позицию. На этом Рис.1 изображен маршрут 1423, он же 3241 (числа в Таблице 1)
Интерес главным образом представляет распределение вблизи наилучшего результата - действительно ли надо перебирать все-все варианты, чтобы найти тот единственный. "Так и случилось", вблизи оптимума есть достаточно удовлетворительных решений. Более того, основная масса результатов отличается от оптимального (наименьшего) не на порядки и даже не в разы. В принципе можно сконструировать такое расположение городов, что оптимум будет сильно отличаться от соседей, но это уже другая задача - поискать трудностей.
То есть все варианты в ужасном количестве слабо отличаются друг от друга и даже крайние не так чтобы очень. На что же надеются те, кто настаивают на переборе ? На чудо ! А вдруг там, слева, найдется что-нибудь этакое... "малой кровью"... Если бы задачи экономического планирования действительно были похожи на ЗК, то без сплошного перебора вполне можно обойтись - чуда все равно не произойдет.
И все же ЗК сыграла некоторую роль в этой дискуссии, правда против чудолюбов. На ЗК пробовали и пробуют всякие разные методы, сокращающие количество вариантов до разумного. Например совершенно очевидно, что в общем случае лучше следующий город выбирать из ближайших, чем из самых дальних. Поскольку ближайших всегда несколько (порядка 6), то уже получаются отнюдь не факториалы. И т.д. Самыми же эффективными для решения ЗК оказались генетические алгоритмы, которые собственно тему закрыли совсем
Таблица 1. Несколько примеров для 4-х городов.
Первый столбец - порядок следования, последующие - длины всех возможных путей (запускал скрипт несколько раз, меняя случайным образом размещение городов)
1234 30.641
1243 43.256
1324 31.645
1342 44.750
1423 41.936
1432 42.425
2134 32.828
2143 43.119
2314 31.507
2341 42.425
2413 44.123
2431 44.750
3124 32.338
3142 44.123
3214 30.014
3241 41.936
3412 43.119
3421 43.256
4123 30.014
4132 31.507
4213 32.338
4231 31.645
4312 32.828
4321 30.641
38.716
37.499
35.203
33.089
35.595
34.698
32.898
33.289
30.993
34.698
29.776
33.089
33.794
29.776
35.403
35.595
33.289
37.499
35.403
30.993
33.794
35.203
32.898
38.716
33.693
22.648
23.298
23.179
22.766
33.692
37.594
37.062
37.713
33.692
26.668
23.179
26.669
26.668
37.182
22.766
37.062
22.648
37.182
37.713
26.669
23.298
37.594
33.693

Это результаты для 5 городов, их уже проще (5!=120) воспринимать на глаз. видно что никаких сверхглубоких минимумов нет.
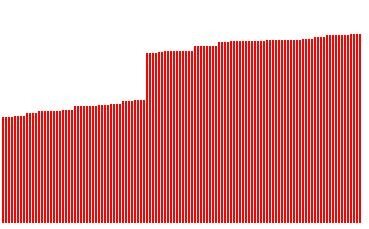
Еще раз пути через 5 городов, но уже отсортированные в порядке возрастания длины. Слева кратчайший, он же наилучший. Далее все отсортированные.

Это для 6 городов (6!=720) так что пришлось уменьшить ширину столбца.

Это для 8 городов (8!=40320), причем я не стал масштабировать, а отобразил по 80 первых результатов из тысячи, т.е. 0..80, 1000..1080, 2000..2080 и т.д. Самый интересный опять-таки слева.
.
В свете вышеизложенного lex-kravetski опять запалил дискуссию о планировании экономики и опять с тем же результатом - то есть все остались при своем мнении. "Убежденные" рыночники невзирая на всю шизовость аргументации настаивают, что задача оптимизации плана на миллионы товарных позиций требует ресурсов и времени на порядки больше, чем имеется во Вселенной. Часто в пример неподъемности ссылаются на задачу коммивояжера (ЗК), которой еще сам Гамильтон баловался. Антирыночники пытаются рассказать о надуманности такой аналогии, но на словах выходит не очень убедительно.
Коммивояжер должен по разу посетить несколько городов, надо найти такой порядок посещения, чтоб суммарный путь был наикратчайшим. Эта простая на первый взгляд задача аналитического решения вроде бы не имеет, а просто перебрать все комбинации затруднительно: при N городов число возможных путей (перестановок) 1*2*3*4*..*(N-1)*N = N!
20! = 2432902008176640000. Если один расчет в наносекунду, то перебор маршуртов через 20 городов займет 2.5 миллиарда секунд - лет 70. Ну а 30! = 265252859812191058636308480000000, в 100 триллионов раз больше. "И не сосчитаешь !"
Все же я решил пощупать страшную задачу руками.

Накидал скрипт, перебирающий все перестановки, поместил случайным образом "города" в квадрате 10x10 и запустил подсчет длины всех возможных путей. В моем варианте коммивояжер как бы выдвигался из точки (0, 0), проезжал через все N городов и возвращался на исходную позицию. На этом Рис.1 изображен маршрут 1423, он же 3241 (числа в Таблице 1)
Интерес главным образом представляет распределение вблизи наилучшего результата - действительно ли надо перебирать все-все варианты, чтобы найти тот единственный. "Так и случилось", вблизи оптимума есть достаточно удовлетворительных решений. Более того, основная масса результатов отличается от оптимального (наименьшего) не на порядки и даже не в разы. В принципе можно сконструировать такое расположение городов, что оптимум будет сильно отличаться от соседей, но это уже другая задача - поискать трудностей.
То есть все варианты в ужасном количестве слабо отличаются друг от друга и даже крайние не так чтобы очень. На что же надеются те, кто настаивают на переборе ? На чудо ! А вдруг там, слева, найдется что-нибудь этакое... "малой кровью"... Если бы задачи экономического планирования действительно были похожи на ЗК, то без сплошного перебора вполне можно обойтись - чуда все равно не произойдет.
И все же ЗК сыграла некоторую роль в этой дискуссии, правда против чудолюбов. На ЗК пробовали и пробуют всякие разные методы, сокращающие количество вариантов до разумного. Например совершенно очевидно, что в общем случае лучше следующий город выбирать из ближайших, чем из самых дальних. Поскольку ближайших всегда несколько (порядка 6), то уже получаются отнюдь не факториалы. И т.д. Самыми же эффективными для решения ЗК оказались генетические алгоритмы, которые собственно тему закрыли совсем
Таблица 1. Несколько примеров для 4-х городов.
Первый столбец - порядок следования, последующие - длины всех возможных путей (запускал скрипт несколько раз, меняя случайным образом размещение городов)
1234 30.641
1243 43.256
1324 31.645
1342 44.750
1423 41.936
1432 42.425
2134 32.828
2143 43.119
2314 31.507
2341 42.425
2413 44.123
2431 44.750
3124 32.338
3142 44.123
3214 30.014
3241 41.936
3412 43.119
3421 43.256
4123 30.014
4132 31.507
4213 32.338
4231 31.645
4312 32.828
4321 30.641
38.716
37.499
35.203
33.089
35.595
34.698
32.898
33.289
30.993
34.698
29.776
33.089
33.794
29.776
35.403
35.595
33.289
37.499
35.403
30.993
33.794
35.203
32.898
38.716
33.693
22.648
23.298
23.179
22.766
33.692
37.594
37.062
37.713
33.692
26.668
23.179
26.669
26.668
37.182
22.766
37.062
22.648
37.182
37.713
26.669
23.298
37.594
33.693

Это результаты для 5 городов, их уже проще (5!=120) воспринимать на глаз. видно что никаких сверхглубоких минимумов нет.

Еще раз пути через 5 городов, но уже отсортированные в порядке возрастания длины. Слева кратчайший, он же наилучший. Далее все отсортированные.

Это для 6 городов (6!=720) так что пришлось уменьшить ширину столбца.

Это для 8 городов (8!=40320), причем я не стал масштабировать, а отобразил по 80 первых результатов из тысячи, т.е. 0..80, 1000..1080, 2000..2080 и т.д. Самый интересный опять-таки слева.