Квантовый ликбез 24. Квантовые гейты.
Предыдущие посты
Рассуждая о классических компьютерах, мы говорили, что любое, сколь угодно сложное вычисление, может быть организовано с помощью ограниченного базисного набора элементарных операций - гейтов. То же самое справедливо и для квантовых вычислений. С некоторыми квантовыми гейтами мы уже бегло ознакомились, когда изучали квантовую телепортацию. Теперь давайте немного эту информацию систематизируем.
Начнём с однокубитных операций. Классический бит может находиться в состоянии либо «0», либо «1», третьего, как говориться, не дано. Стало быть, единственное, что с битом можно сделать, это изменить его состояние на противоположное.
Маленькое уточнение: на самом деле можно ещё принудительно установить бит в состояние «0» или «1». Это операции записи, мы их будем применять, конечно, но в число гейтов включать не будем. Также оставим за скобками вариант, формально эквивалентный применению «единичного» гейта, а на практике заключающийся в том, чтобы не делать с битом или кубитом ничего.
Итак, с учётом уточнения, существует только один однобитный гейт - «NOT».
Кубит может находится в квантовой суперпозиции групп витруальных вариантов |0〉 и |1〉:
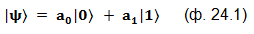
«Доля» каждой из групп определяется двумя комплексными числами - амплитудами вероятности a0 и a1. Эти числа могут быть, в принципе, любыми. Значит, для кубита количество возможных квантовых состояний вида |ψ〉 бесконечно.
Также бесконечно количество разрешенных однокубитных операций, которые, по сути дела, просто определённым образом изменяют значения амплитуд вероятности a0 и a1. При моделировании квантового компьютера будем считать, что мы умеем совершать над кубитом всевозможные однокубитные операции. Единственное ограничение, накладываемое квантовой физикой на такие операции, это требование унитарности. Глубого копать в сторону понятия унитарности нам резона нет, но заметим, что унитарность обеспечивается обратимыми операциями, которые мы изучали в предыдущей части. Для более продвинутых скажем, что унитарные операции математически идентичны повороту вектора квантового состояния в условном пространстве, без изменения длины (модуля) вектора (смотрим часть 17-4).
На практике операции реализуются путём «дозированных» физических воздействий на кубит, типа тех, что мы изучали в части 16. Любое такое воздействие, напомню, описывается матрицей следующего вида:

Два числа в верхней строке показывают, как воздействие-операция изменяет группу |0〉. Два числа в нижней строке показывают, как изменяется группа |1〉. То есть, в общем случае для описания любой однокубитной операции достаточно этого набора из четырёх чисел. Для удобства некоторым, наиболее часто используемым операциям и их матрицам, присвоены особые обозначения.
Например, гейт [X], он же - квантовый «NOT» - гейт, описывается вот такой матрицей:

Давайте ещё раз постмотрим, как гейт [X] воздействует на состояние |ψ〉 (ф. 24.1.):
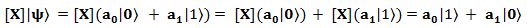
В результате воздействия [X] группы |0〉 и |1〉 «обменялись» амплитудами вероятности. Или можно взглянуть на это дело в другом ракурсе: воздействие [X] превратило группу |0〉 в группу |1〉, а группу |1〉, наоборот, в группу |0〉. Для полной ясности изобразим действие гейта [X] на следующей диаграмме:
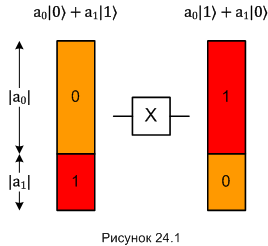
Если забыли, как надо понимать такие диаграммы, посмотрите ещё раз часть 21-2.
В дальнейшем нам предстоит рисовать квантовые вычислительные схемы. Они по виду будут аналогичны классическим схемам (см. часть 22). В частности, однокубитные операции будем изображать в виде прямоугольников с символом операции внутри. Как показано на том же рисунке 24.1.
Ещё одна важная однокубитная операция - гейт Адамара [H]. Вот матрица это гейта:
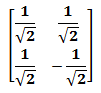
Особенность этого гейта заключается в том, что он, с одной стороны, превращает определённые состояния кубита |0〉 и |1〉 в состояния с максимальной степенью неопределённости:
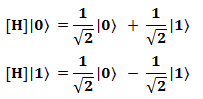
А с другой стороны, наоборот, превращает максимально неопределённое состояние в определённое, например:
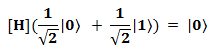
Воздействие гейта [H] на произвольное однокубитное состояние типа (ф. 24.1) показано на следующей диаграмме:
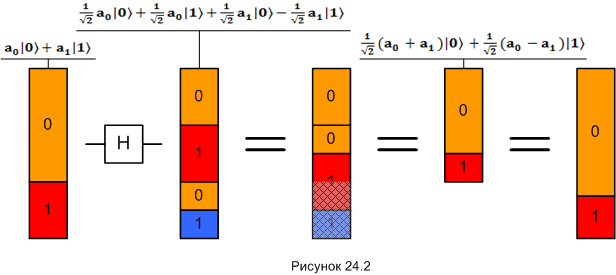
Нужны, наверное, пояснения. На первом рисунке (считаем слева на право) показано исходное состояние кубита. Второй и последующий рисунки - состояние после воздействия [H]. На третьем рисунке области диаграммы упорядочены. Также заштрихованы «кусочки» группы |1〉 с положительным и отрицательным знаком, которые в силу суперпозиции «съедают» друг друга. На четвёртом рисунке состояние кубита показано уже без этих кусочков. Ну а пятый рисунок просто масштабирован по высоте, чтобы вы могли наглядно сравнить исходное состояние и то, что получилось в результате воздействия.
Позже нам потребуются ещё кое-какие однокубитные гейты, мы их рассмотрим по мере необходимости.
Из двухкубитных операций мы задействуем всего одну: гейт «CNOT». Если матрица однобитной операции имеет размерность 2х2 (четыре числа), то матрица двухкубитной операции имеет уже размерность 4х4 (16 чисел). Но физический смысл чисел в матрице тот же: каждая строка матрицы показывает, в какой пропорции воздействие «расщепляет» то или иное базисное двухкубитное состояние. Матрица гейта «CNOT» выглядит так:
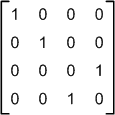
При этом подразумевается, что:
- первая (верхняя) строка показывает, как воздействие расщепляет базисное состояние |00〉;
- вторая строка - расщепление базисного состояния |01〉;
- третья строка - расщепление базисного состояния |10〉;
- четвёртая строка - расщепление базисного состояния |11〉.
Логика работы гейта «CNOT» заключается в следующем. Операция никак «не затрагивает» группы |00〉 и |01〉, те, где контролирующий кубит равен нулю. А в тех группах, в которых контролирующий кубит равен единице - |10〉 и |11〉 - операция инвертирует значение рабочего бита. Иными словами, гейт «CNOT» превращает базисное состояние |10〉 в состояние |11〉 и наоборот.
На квантовых схемах гейт «CNOT» изображается так же, как и на классических:
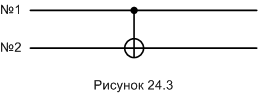
В такой конфигурации кубит №1 - контролирующий, кубит №2 - «рабочий».
Разбирая классический «CNOT» мы говорили, что состояние контролирующего бита в результате операции не изменяется. Так вот, обращаю особое внимание на то, в квантовом случае ЭТО НЕ ТАК. Точнее, не всегда так. Смотрите, допустим, у нас имеется два кубита, «A» и «B», в следующих чистых состояниях:
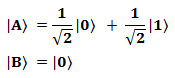
Кубиты не запутаны друг с другом. Сепарабельное двухкубитное состояние системы |AB〉 мы можем записать как произведение однокубитных состояний |A〉 и |B〉:
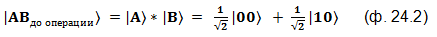
Теперь применим к этим двум кубитам операцию «CNOT». Пусть при этом кубит «А» будет контрольным, кубит «B» - рабочим. В результате операции получаем:
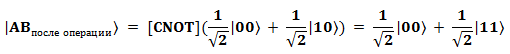
Это уже не сепарабельное, а самое что ни на есть запутанное состояние. Таким образом мы запутали два «чистых» кубита в единую двухкубитную систему. Состояние и рабочего, и контролирующего кубита изменились - были чистыми, стали смешанными.
По сложившейся традидии изобразим работу гейта «CNOT» над состоянием (ф. 24.2) в виде диаграммы:
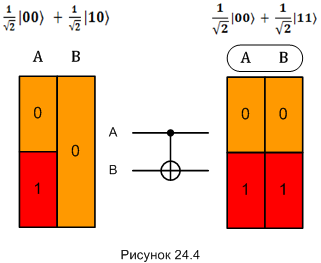
На правой диаграмме символы «А» и «B» обведены овальчиком - это чтобы показать, что кубиты запутались.
Однокубитные гейты в купе с двухкубитным гейтом «CNOT» уже составляют базис операций, достаточный для организации любых квантовых вычислений с кубитовым регистром какого угодно размера. Однако мы будем использовать при построении квантового компьютера ещё трёхкубитный гейт «CCNOT», который называют ещё «гейт Тоффоли». Можно было бы обойтись и без него, но тогда вычислительные схемы будут выглядеть более громоздко и менее «усвояемо».
Матрица трёхкубитной операции «CCNOT» имеет размерность 8х8 (64 числа):

В гейте «CCNOT» два контролирующих кубита и один рабочий. Операция изменяет только те базисные состояния, где оба контролирующих бита равны единице. А именно, заставляет базисные состояния |110〉 и |111〉 «обменяться» амплитудами вероятности (смотрите две нижнох строки матрицы). Остальные шесть базисных состояний гейт «CCNOT» оставляет неизменными.
На схемах гейт «CCNOT» изображают так:
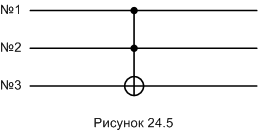
Здесь кубиты №1 и №2 - контролирующие, кубит №3 - рабочий.
Посмотрим, как гейт «CCNOT» действует на некоторое трёхкубитное состояние:
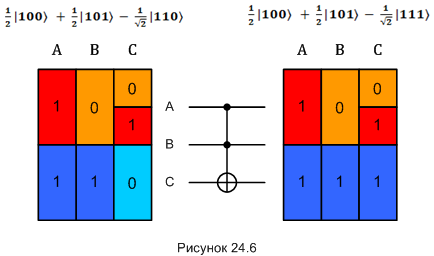
В следующей части мы уже начнём разбираться, как из этих и прочих квантовых гейтов собрать квантовый компьютер.
Продолжение
Рассуждая о классических компьютерах, мы говорили, что любое, сколь угодно сложное вычисление, может быть организовано с помощью ограниченного базисного набора элементарных операций - гейтов. То же самое справедливо и для квантовых вычислений. С некоторыми квантовыми гейтами мы уже бегло ознакомились, когда изучали квантовую телепортацию. Теперь давайте немного эту информацию систематизируем.
Начнём с однокубитных операций. Классический бит может находиться в состоянии либо «0», либо «1», третьего, как говориться, не дано. Стало быть, единственное, что с битом можно сделать, это изменить его состояние на противоположное.
Маленькое уточнение: на самом деле можно ещё принудительно установить бит в состояние «0» или «1». Это операции записи, мы их будем применять, конечно, но в число гейтов включать не будем. Также оставим за скобками вариант, формально эквивалентный применению «единичного» гейта, а на практике заключающийся в том, чтобы не делать с битом или кубитом ничего.
Итак, с учётом уточнения, существует только один однобитный гейт - «NOT».
Кубит может находится в квантовой суперпозиции групп витруальных вариантов |0〉 и |1〉:
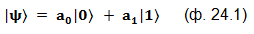
«Доля» каждой из групп определяется двумя комплексными числами - амплитудами вероятности a0 и a1. Эти числа могут быть, в принципе, любыми. Значит, для кубита количество возможных квантовых состояний вида |ψ〉 бесконечно.
Также бесконечно количество разрешенных однокубитных операций, которые, по сути дела, просто определённым образом изменяют значения амплитуд вероятности a0 и a1. При моделировании квантового компьютера будем считать, что мы умеем совершать над кубитом всевозможные однокубитные операции. Единственное ограничение, накладываемое квантовой физикой на такие операции, это требование унитарности. Глубого копать в сторону понятия унитарности нам резона нет, но заметим, что унитарность обеспечивается обратимыми операциями, которые мы изучали в предыдущей части. Для более продвинутых скажем, что унитарные операции математически идентичны повороту вектора квантового состояния в условном пространстве, без изменения длины (модуля) вектора (смотрим часть 17-4).
На практике операции реализуются путём «дозированных» физических воздействий на кубит, типа тех, что мы изучали в части 16. Любое такое воздействие, напомню, описывается матрицей следующего вида:

Два числа в верхней строке показывают, как воздействие-операция изменяет группу |0〉. Два числа в нижней строке показывают, как изменяется группа |1〉. То есть, в общем случае для описания любой однокубитной операции достаточно этого набора из четырёх чисел. Для удобства некоторым, наиболее часто используемым операциям и их матрицам, присвоены особые обозначения.
Например, гейт [X], он же - квантовый «NOT» - гейт, описывается вот такой матрицей:

Давайте ещё раз постмотрим, как гейт [X] воздействует на состояние |ψ〉 (ф. 24.1.):
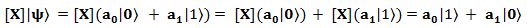
В результате воздействия [X] группы |0〉 и |1〉 «обменялись» амплитудами вероятности. Или можно взглянуть на это дело в другом ракурсе: воздействие [X] превратило группу |0〉 в группу |1〉, а группу |1〉, наоборот, в группу |0〉. Для полной ясности изобразим действие гейта [X] на следующей диаграмме:

Если забыли, как надо понимать такие диаграммы, посмотрите ещё раз часть 21-2.
В дальнейшем нам предстоит рисовать квантовые вычислительные схемы. Они по виду будут аналогичны классическим схемам (см. часть 22). В частности, однокубитные операции будем изображать в виде прямоугольников с символом операции внутри. Как показано на том же рисунке 24.1.
Ещё одна важная однокубитная операция - гейт Адамара [H]. Вот матрица это гейта:
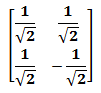
Особенность этого гейта заключается в том, что он, с одной стороны, превращает определённые состояния кубита |0〉 и |1〉 в состояния с максимальной степенью неопределённости:
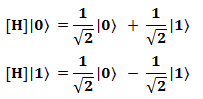
А с другой стороны, наоборот, превращает максимально неопределённое состояние в определённое, например:
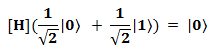
Воздействие гейта [H] на произвольное однокубитное состояние типа (ф. 24.1) показано на следующей диаграмме:

Нужны, наверное, пояснения. На первом рисунке (считаем слева на право) показано исходное состояние кубита. Второй и последующий рисунки - состояние после воздействия [H]. На третьем рисунке области диаграммы упорядочены. Также заштрихованы «кусочки» группы |1〉 с положительным и отрицательным знаком, которые в силу суперпозиции «съедают» друг друга. На четвёртом рисунке состояние кубита показано уже без этих кусочков. Ну а пятый рисунок просто масштабирован по высоте, чтобы вы могли наглядно сравнить исходное состояние и то, что получилось в результате воздействия.
Позже нам потребуются ещё кое-какие однокубитные гейты, мы их рассмотрим по мере необходимости.
Из двухкубитных операций мы задействуем всего одну: гейт «CNOT». Если матрица однобитной операции имеет размерность 2х2 (четыре числа), то матрица двухкубитной операции имеет уже размерность 4х4 (16 чисел). Но физический смысл чисел в матрице тот же: каждая строка матрицы показывает, в какой пропорции воздействие «расщепляет» то или иное базисное двухкубитное состояние. Матрица гейта «CNOT» выглядит так:

При этом подразумевается, что:
- первая (верхняя) строка показывает, как воздействие расщепляет базисное состояние |00〉;
- вторая строка - расщепление базисного состояния |01〉;
- третья строка - расщепление базисного состояния |10〉;
- четвёртая строка - расщепление базисного состояния |11〉.
Логика работы гейта «CNOT» заключается в следующем. Операция никак «не затрагивает» группы |00〉 и |01〉, те, где контролирующий кубит равен нулю. А в тех группах, в которых контролирующий кубит равен единице - |10〉 и |11〉 - операция инвертирует значение рабочего бита. Иными словами, гейт «CNOT» превращает базисное состояние |10〉 в состояние |11〉 и наоборот.
На квантовых схемах гейт «CNOT» изображается так же, как и на классических:

В такой конфигурации кубит №1 - контролирующий, кубит №2 - «рабочий».
Разбирая классический «CNOT» мы говорили, что состояние контролирующего бита в результате операции не изменяется. Так вот, обращаю особое внимание на то, в квантовом случае ЭТО НЕ ТАК. Точнее, не всегда так. Смотрите, допустим, у нас имеется два кубита, «A» и «B», в следующих чистых состояниях:
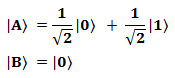
Кубиты не запутаны друг с другом. Сепарабельное двухкубитное состояние системы |AB〉 мы можем записать как произведение однокубитных состояний |A〉 и |B〉:
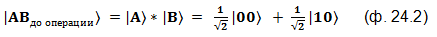
Теперь применим к этим двум кубитам операцию «CNOT». Пусть при этом кубит «А» будет контрольным, кубит «B» - рабочим. В результате операции получаем:
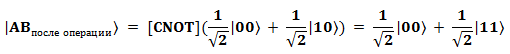
Это уже не сепарабельное, а самое что ни на есть запутанное состояние. Таким образом мы запутали два «чистых» кубита в единую двухкубитную систему. Состояние и рабочего, и контролирующего кубита изменились - были чистыми, стали смешанными.
По сложившейся традидии изобразим работу гейта «CNOT» над состоянием (ф. 24.2) в виде диаграммы:

На правой диаграмме символы «А» и «B» обведены овальчиком - это чтобы показать, что кубиты запутались.
Однокубитные гейты в купе с двухкубитным гейтом «CNOT» уже составляют базис операций, достаточный для организации любых квантовых вычислений с кубитовым регистром какого угодно размера. Однако мы будем использовать при построении квантового компьютера ещё трёхкубитный гейт «CCNOT», который называют ещё «гейт Тоффоли». Можно было бы обойтись и без него, но тогда вычислительные схемы будут выглядеть более громоздко и менее «усвояемо».
Матрица трёхкубитной операции «CCNOT» имеет размерность 8х8 (64 числа):

В гейте «CCNOT» два контролирующих кубита и один рабочий. Операция изменяет только те базисные состояния, где оба контролирующих бита равны единице. А именно, заставляет базисные состояния |110〉 и |111〉 «обменяться» амплитудами вероятности (смотрите две нижнох строки матрицы). Остальные шесть базисных состояний гейт «CCNOT» оставляет неизменными.
На схемах гейт «CCNOT» изображают так:

Здесь кубиты №1 и №2 - контролирующие, кубит №3 - рабочий.
Посмотрим, как гейт «CCNOT» действует на некоторое трёхкубитное состояние:

В следующей части мы уже начнём разбираться, как из этих и прочих квантовых гейтов собрать квантовый компьютер.
Продолжение