Квантовый ликбез - 16-2. Разные разности.
Предыдущие посты
Часть 16 в один пост не влезла, это второй.
Но вернёмся к эксперименту, мы ещё не «выдоили» всю информацию, которую он может дать. Теперь сделаем длинную серию попыток с тем же воздействием [W] на частицу и определим вероятности результатов 〈0+〉 и 〈0-〉.
Затем проводим следующую серию попыток, изменив время воздействия магнитного поля на частицу. Силу и направление магнитного поля менять не будем. Проделав необходимое количество таких серий, каждую со своим временем воздействия, и зафиксировав в каждой из них вероятности результатов 〈0+〉 и 〈0-〉, мы сможем построить вот такой график:
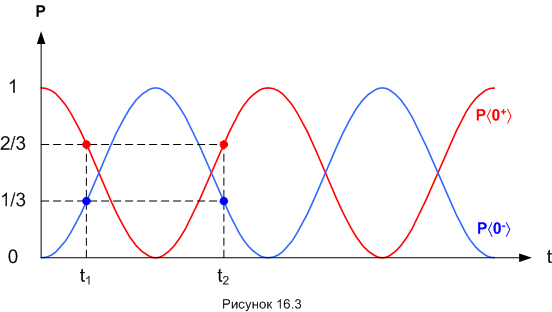
Наблюдаем циклическую зависимость вероятностей результатов от времени воздействия. Для порядка напишем теоретические формулы этих зависимостей:

Здесь k - это некий коэффициент, зависящий от интенсивности и направления магнитного поля. Поскольку этих настроек мы в ходе эксперимента не изменяем, то коэффициент считаем постоянной величиной.
Вероятности результатов 〈0+〉 и 〈0-〉 в сумме дают единицу, как и положено.
В этом эксперименте мы пользовались самоочевидным правилом: одинаковые квантовые состояния обеспечивают одинаковые вероятности результатов измерения. Но обратное в общем случае не верно. Это следующая важная вещь, о которой необходимо сказать: одинаковые вероятности результатов измерения не гарантируют одинаковости измеряемых состояний. Или то же самое, «вид сбоку»: разные квантовые состояния могут давать одинаковые вероятности результатов.
Посмотрим ещё раз на рисунок 16.3. На графике отмечены две точки, соответствующие сериям с длительностями воздействий t1 и t2. Давайте обозначим эти разные воздействия так: [W1] и [W2], а квантовое состояние частицы после таких воздействий обозначим как |SW1〉 и |SW2〉 соответственно. Распределение результатов 〈0+〉 и 〈0-〉 в серии после воздействий [W1] и [W2] одинаково:

Но одинаковы ли квантовые состояния |SW1〉 и |SW2〉? Нет! Чтобы в этом убедиться, проведём следующий эксперимент.

Здесь мы в каждой попытке воздействуем на частицу со спином |0+〉 два раза подряд, а затем измеряем момент импульса прибором П2. На первом этапе эксперимента (рисунок 16.4-а) мы в каждой попытке дважды подвергнем частицу воздействию [W1]. Первое воздействие мы делаем для того, чтобы получить частицу в состоянии |SW1〉. А второе воздействие переводит состояние |SW1〉 в какое-то новое состояние |SW1W1〉. Эти операции мы формализуем вот такой записью:
[W1][W1]|0+〉 = [W1]|SW1〉 = |SW1W1〉
Всё понятно? Двукратное воздействие [W1] на состояние |0+〉 равносильно однократному воздействию на состояние |SW1〉, и то, и другое приводит к состоянию |SW1W1〉. Вот это состояние мы и измеряем прибором П2 с ориентацией {0}. Сделав на первом этапе эксперимента множество таких попыток, мы узнаем, как распределяются результаты такого измерения. Распределение по ансамблю «|SW1W1〉» может быть, например, таким:

Второй этап (рисунок 16.4-б) проводим аналогично первому с одни лишь отличием: первое воздействие будет [W2]. Стало быть, после первого воздействия мы получаем состояние:
[W2]|0+〉 = |SW2〉
А после второго воздействия получаем состояние:
[W1][W2]|0+〉 = [W1]|SW2〉 = |SW2W1〉
Обратите внимание на порядок в левой части формулы: воздействия записываются справа налево. В нашем случае сначала идёт [W2], затем [W1].
И вот это состояние |SW2W1〉 мы измеряем. После множества попыток мы можем увидеть вот такое, например, распределение результатов:

Сравнивая итоги первого и второго этапа, делаем вывод: состояния |SW1W1〉 и |SW2W1〉 - разные. Следовательно, состояния |SW1〉 и |SW2〉 разные тоже, что и требовалось доказать (экспериментально!). А на языке математики этот вывод можно сформулировать так (просто, чтобы вы привыкали к обозначениям):
|SW1W1〉≠ |SW1W2〉 → [W1]|SW1〉≠ [W1]|SW2〉 → |SW1〉≠ |SW2〉
Расшифровка этой записи требуется? Тогда я в печали :(
В следующей части ликбеза мы разберём физический механизм этих воздействий и выясним, почему разные квантовые состояния могут давать одинаковую статистику измерений. Ну и продолжим неспешный подъём по ступеням квантовой математики.
Продолжение
Часть 16 в один пост не влезла, это второй.
Но вернёмся к эксперименту, мы ещё не «выдоили» всю информацию, которую он может дать. Теперь сделаем длинную серию попыток с тем же воздействием [W] на частицу и определим вероятности результатов 〈0+〉 и 〈0-〉.
Затем проводим следующую серию попыток, изменив время воздействия магнитного поля на частицу. Силу и направление магнитного поля менять не будем. Проделав необходимое количество таких серий, каждую со своим временем воздействия, и зафиксировав в каждой из них вероятности результатов 〈0+〉 и 〈0-〉, мы сможем построить вот такой график:

Наблюдаем циклическую зависимость вероятностей результатов от времени воздействия. Для порядка напишем теоретические формулы этих зависимостей:

Здесь k - это некий коэффициент, зависящий от интенсивности и направления магнитного поля. Поскольку этих настроек мы в ходе эксперимента не изменяем, то коэффициент считаем постоянной величиной.
Вероятности результатов 〈0+〉 и 〈0-〉 в сумме дают единицу, как и положено.
В этом эксперименте мы пользовались самоочевидным правилом: одинаковые квантовые состояния обеспечивают одинаковые вероятности результатов измерения. Но обратное в общем случае не верно. Это следующая важная вещь, о которой необходимо сказать: одинаковые вероятности результатов измерения не гарантируют одинаковости измеряемых состояний. Или то же самое, «вид сбоку»: разные квантовые состояния могут давать одинаковые вероятности результатов.
Посмотрим ещё раз на рисунок 16.3. На графике отмечены две точки, соответствующие сериям с длительностями воздействий t1 и t2. Давайте обозначим эти разные воздействия так: [W1] и [W2], а квантовое состояние частицы после таких воздействий обозначим как |SW1〉 и |SW2〉 соответственно. Распределение результатов 〈0+〉 и 〈0-〉 в серии после воздействий [W1] и [W2] одинаково:

Но одинаковы ли квантовые состояния |SW1〉 и |SW2〉? Нет! Чтобы в этом убедиться, проведём следующий эксперимент.

Здесь мы в каждой попытке воздействуем на частицу со спином |0+〉 два раза подряд, а затем измеряем момент импульса прибором П2. На первом этапе эксперимента (рисунок 16.4-а) мы в каждой попытке дважды подвергнем частицу воздействию [W1]. Первое воздействие мы делаем для того, чтобы получить частицу в состоянии |SW1〉. А второе воздействие переводит состояние |SW1〉 в какое-то новое состояние |SW1W1〉. Эти операции мы формализуем вот такой записью:
[W1][W1]|0+〉 = [W1]|SW1〉 = |SW1W1〉
Всё понятно? Двукратное воздействие [W1] на состояние |0+〉 равносильно однократному воздействию на состояние |SW1〉, и то, и другое приводит к состоянию |SW1W1〉. Вот это состояние мы и измеряем прибором П2 с ориентацией {0}. Сделав на первом этапе эксперимента множество таких попыток, мы узнаем, как распределяются результаты такого измерения. Распределение по ансамблю «|SW1W1〉» может быть, например, таким:

Второй этап (рисунок 16.4-б) проводим аналогично первому с одни лишь отличием: первое воздействие будет [W2]. Стало быть, после первого воздействия мы получаем состояние:
[W2]|0+〉 = |SW2〉
А после второго воздействия получаем состояние:
[W1][W2]|0+〉 = [W1]|SW2〉 = |SW2W1〉
Обратите внимание на порядок в левой части формулы: воздействия записываются справа налево. В нашем случае сначала идёт [W2], затем [W1].
И вот это состояние |SW2W1〉 мы измеряем. После множества попыток мы можем увидеть вот такое, например, распределение результатов:

Сравнивая итоги первого и второго этапа, делаем вывод: состояния |SW1W1〉 и |SW2W1〉 - разные. Следовательно, состояния |SW1〉 и |SW2〉 разные тоже, что и требовалось доказать (экспериментально!). А на языке математики этот вывод можно сформулировать так (просто, чтобы вы привыкали к обозначениям):
|SW1W1〉≠ |SW1W2〉 → [W1]|SW1〉≠ [W1]|SW2〉 → |SW1〉≠ |SW2〉
Расшифровка этой записи требуется? Тогда я в печали :(
В следующей части ликбеза мы разберём физический механизм этих воздействий и выясним, почему разные квантовые состояния могут давать одинаковую статистику измерений. Ну и продолжим неспешный подъём по ступеням квантовой математики.
Продолжение