Квантовый ликбез - 17-1. Вектор квантового состояния
Предыдущие посты
В предыдущей части мы увидели, как воздействие на квантовый объект, пребывающий в известном экспериментатору состоянии, проявляется в классической реальности: изменяется вероятность того или иного результата измерения. Теперь давайте копнём глубже и посмотрим, что происходит в квантовой реальности.
«Посмотрим» - это, конечно, не надо понимать буквально. Как уже неоднократно говорилось, прямо заглянуть в квантовую реальность никакой возможности нет. Квантовый объект для нас - это навсегда «черный ящик». Зато можно поиграть с этим «ящиком», подвергая его всяческим воздействиям и наблюдая за его реакцией. Набрав достаточное количество таких наблюдений, мы уже сможем строить какие-то гипотезы о «внутренностях» квантового объекта. Собственно, те постулаты, которые были тут сформулированы, и те вещи, о которых мы будем говорить в этой части, являются как раз теоретическим результатом огромного множества таких вот экспериментальных игр.
Как я уже пугал - в этой части я изрядно нагружу вас формулами. Кто не забоялся - ныряете под кат.
Вернёмся к экспериментам (рис. 16.4) из предыдущей части. Их схемы повторно показаны на рисунке 17.1.
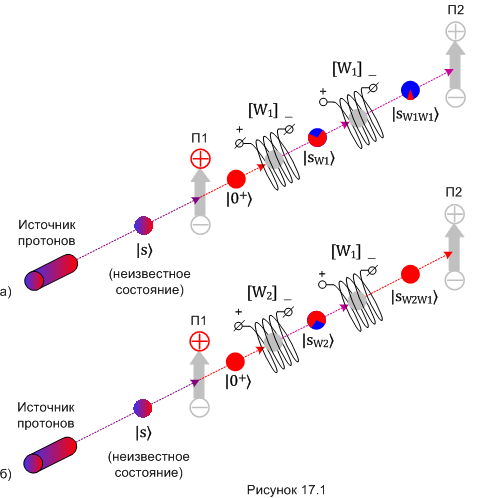
Сначала рассмотрим ещё раз случай «а». Перед первым воздействием, на входе магнита, спин частицы пребывает в состоянии |0+〉. Напомню: мы специально готовим это состояние с помощью первого измерения и отсева частиц со спином |0-〉.
В состоянии |0+〉 квантовые вектора вариантов группы |0+〉 складываются в конструктивную суперпозицию. Квантовые вектора группы |0-〉 находятся в состоянии деструктивной суперпозиции, то есть, полностью компенсируют друг друга. Можно изобразить эту ситуацию в виде следующей диаграммы (рисунок 17.2):
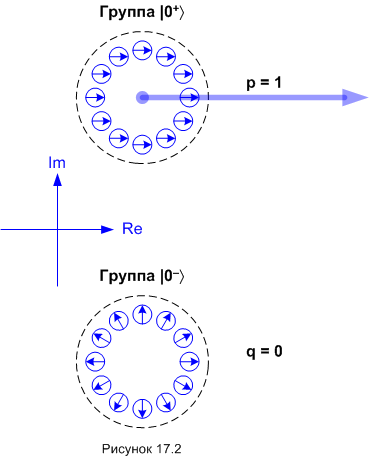
Как и раньше, синими кружочками показаны виртуальные варианты. Синяя стрелочка в кружочке показывает направление квантового вектора данного виртуального варианта в условном математическом пространстве. Оно, пространство это, также обозначено на рисунке осями «Re» и «Im». Не лишним, пожалуй, будет напомнить, что на самом деле в каждой группе бесконечное число виртуальных вариантов. На рисунке их всего по двенадцать, так что сами опять домыслите эту картинку до бесконечностей.
Квантовые вектора одной группы, как мы давно знаем, складываются в групповой квантовый вектор - амплитуду вероятности. Амплитуду вероятности группы |0+〉 обозначим буквой «p», амплитуду вероятности группы |0-〉 - буквой «q».
Амплитуда вероятности единственной реализуемой группы |0+〉 равна единице, она показана толстой синей стрелкой. У группы |0-〉 никакой толстой стрелки нет. Разнонаправленные квантовые вектора «скушали друг друга» в деструктивной суперпозиции, поэтому амплитуда вероятности этой группы равна нулю.
Хочу обратить ваше внимание вот на что. Конкретное направление единственного вектора амплитуды вероятности в условном пространстве в данном случае несущественно. Законы квантовой механики предоставляют нам полное право изобразить диаграмму, например, вот так:
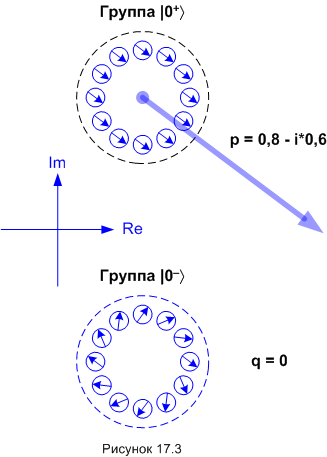
Мы просто взяли диаграмму 17.2, повернули все квантовые вектора на один и тот же угол и получили диаграмму 17.3. С точки зрения возможных результатов измерений и результатов различных воздействий на квантовое состояние физические ситуации на рисунках 17.2 и 17.3 совершенно неотличимы. Поэтому поворот квантовых векторов ВСЕХ виртуальных вариантов на один и тот же угол не меняет квантового состояния. Поэтому же, не смотря на то, что квантовые вектора, а значит и вектора амплитуд вероятности безостановочно вращаются в условном пространстве (смотрим часть 10), квантовое состояние остаётся стационарным. Тут можно провести аналогию со звуком. Амплитуда звуковой волны постоянно меняется, но если она меняется с определённой частотой, мы будем слышать одну и ту же чистую ноту.
Да, обратите внимание: все вектора мы повернули, но направление осей условного пространства (комплексной плоскости) сохранили. То есть, вектор амплитуды вероятности группы |0+〉 провернулся на комплексной плоскости. До поворота он был параллелен оси Re и выражался действительным числом - единицей. Теперь же вектор обладает как действительной, так и мнимой частями и выражается комплексным числом:
p = 0,8 + i*0,6
Но длина вектора (модуль комплексного числа) осталась равной единице. Можете сами проверить, сложив квадраты реальной и мнимой частей. Соответственно и вероятность получить при измерении результат 〈0+〉 так же равна единице.
Продолжение части 17
В предыдущей части мы увидели, как воздействие на квантовый объект, пребывающий в известном экспериментатору состоянии, проявляется в классической реальности: изменяется вероятность того или иного результата измерения. Теперь давайте копнём глубже и посмотрим, что происходит в квантовой реальности.
«Посмотрим» - это, конечно, не надо понимать буквально. Как уже неоднократно говорилось, прямо заглянуть в квантовую реальность никакой возможности нет. Квантовый объект для нас - это навсегда «черный ящик». Зато можно поиграть с этим «ящиком», подвергая его всяческим воздействиям и наблюдая за его реакцией. Набрав достаточное количество таких наблюдений, мы уже сможем строить какие-то гипотезы о «внутренностях» квантового объекта. Собственно, те постулаты, которые были тут сформулированы, и те вещи, о которых мы будем говорить в этой части, являются как раз теоретическим результатом огромного множества таких вот экспериментальных игр.
Как я уже пугал - в этой части я изрядно нагружу вас формулами. Кто не забоялся - ныряете под кат.
Вернёмся к экспериментам (рис. 16.4) из предыдущей части. Их схемы повторно показаны на рисунке 17.1.

Сначала рассмотрим ещё раз случай «а». Перед первым воздействием, на входе магнита, спин частицы пребывает в состоянии |0+〉. Напомню: мы специально готовим это состояние с помощью первого измерения и отсева частиц со спином |0-〉.
В состоянии |0+〉 квантовые вектора вариантов группы |0+〉 складываются в конструктивную суперпозицию. Квантовые вектора группы |0-〉 находятся в состоянии деструктивной суперпозиции, то есть, полностью компенсируют друг друга. Можно изобразить эту ситуацию в виде следующей диаграммы (рисунок 17.2):

Как и раньше, синими кружочками показаны виртуальные варианты. Синяя стрелочка в кружочке показывает направление квантового вектора данного виртуального варианта в условном математическом пространстве. Оно, пространство это, также обозначено на рисунке осями «Re» и «Im». Не лишним, пожалуй, будет напомнить, что на самом деле в каждой группе бесконечное число виртуальных вариантов. На рисунке их всего по двенадцать, так что сами опять домыслите эту картинку до бесконечностей.
Квантовые вектора одной группы, как мы давно знаем, складываются в групповой квантовый вектор - амплитуду вероятности. Амплитуду вероятности группы |0+〉 обозначим буквой «p», амплитуду вероятности группы |0-〉 - буквой «q».
Амплитуда вероятности единственной реализуемой группы |0+〉 равна единице, она показана толстой синей стрелкой. У группы |0-〉 никакой толстой стрелки нет. Разнонаправленные квантовые вектора «скушали друг друга» в деструктивной суперпозиции, поэтому амплитуда вероятности этой группы равна нулю.
Хочу обратить ваше внимание вот на что. Конкретное направление единственного вектора амплитуды вероятности в условном пространстве в данном случае несущественно. Законы квантовой механики предоставляют нам полное право изобразить диаграмму, например, вот так:

Мы просто взяли диаграмму 17.2, повернули все квантовые вектора на один и тот же угол и получили диаграмму 17.3. С точки зрения возможных результатов измерений и результатов различных воздействий на квантовое состояние физические ситуации на рисунках 17.2 и 17.3 совершенно неотличимы. Поэтому поворот квантовых векторов ВСЕХ виртуальных вариантов на один и тот же угол не меняет квантового состояния. Поэтому же, не смотря на то, что квантовые вектора, а значит и вектора амплитуд вероятности безостановочно вращаются в условном пространстве (смотрим часть 10), квантовое состояние остаётся стационарным. Тут можно провести аналогию со звуком. Амплитуда звуковой волны постоянно меняется, но если она меняется с определённой частотой, мы будем слышать одну и ту же чистую ноту.
Да, обратите внимание: все вектора мы повернули, но направление осей условного пространства (комплексной плоскости) сохранили. То есть, вектор амплитуды вероятности группы |0+〉 провернулся на комплексной плоскости. До поворота он был параллелен оси Re и выражался действительным числом - единицей. Теперь же вектор обладает как действительной, так и мнимой частями и выражается комплексным числом:
p = 0,8 + i*0,6
Но длина вектора (модуль комплексного числа) осталась равной единице. Можете сами проверить, сложив квадраты реальной и мнимой частей. Соответственно и вероятность получить при измерении результат 〈0+〉 так же равна единице.
Продолжение части 17