Карьера во Власти и формула Байеса
В дискуссии (да, у меня в комментариях все еще бывают дискуссии) с chukcha_digest я сформулировал свою модель "попадания во Власть":
Основной массе населения вход туда заказан, один шанс из ста - это не свободный вход, а отсутствие шанса вообще (о шансах - отдельный пост). Вот об этом я и пишу: если Вы не феодал, у Вас есть шанс. Но его все равно что нет.
Так вот, ниже я хочу пояснить, что значит "есть шанс, но его все равно что нет".
Предположим, что для кооптации во властную группировку уровня N кандидату X требуется достигнуть некоторого градуса доверия со стороны группировки: "скорее не сдаст, чем сдаст". Ну скажем, вероятность 0.95, что не сдаст (меньше нельзя, "это политика, тут и убить могут").
Уверенность, сдаст или нет, можно получить, давая кандидату какие-то полномочия и наблюдая результат (были ли утечки информации или денег, не согласованные с начальством решения и т.д. и т.п). Однако насколько достоверно можно наблюдать этот результат? Ведь если ситуация "все нормально" может быть связана как с тем, что кандидат и в самом деле все сделал правильно, так и с тем, что он просто ловко замел следы. И наоборот, ситуация "что-то не то" может возникнуть и когда в самом деле не то, и когда кандидата тупо подставили (что во властной среде правило, а не исключение). Кроме того, в стремлении втереться в доверие кандидат может какое-то время воздерживаться от предательства, в надежде сорвать крупный куш (в этом смысле "все нормально" даже более подозрительно, чем "что-то не то"). Таким образом, один раз "все нормально" не сильно прибавляет доверия кандидату - "было бы ненормально, вообще убили бы". Насколько "не сильно"?
В терминах теоремы Байеса, "силой" проверки является степень правдоподобия теста - отношение вероятности истинноположительного результата (проверку прошел, потому что верный) к вероятности ложноположительного результата (проверку прошел, потому что хитрый). Первая должна быть чуть больше, чем вторая (иначе проверка ничего не дает); насколько выше? Например, в 1.5 раза (0.6:0.4) для среднего человека - то есть из десяти человек, прошедших тест, шестеро сделали это из верности, а четверо - из хитрости. А если человек не средний, а из хорошей семьи? Такому хочется сделать поблажку ("наверное должен понимать, что верным (до определенного предела) быть выгоднее, чем хитрым") - поэтому тут соотношение будет побольше, допустим, 3 раза (0.75:0.25). Я говорю сейчас о субъективной оценке вероятностей тем представителем группировки, который "ведет" данного кандидата и потом в случае чего отвечает за его верность; объективно все кандидаты могут быть верными или жуликами, для дальнейших расчетов это несущественно.
Зададим далее априорную вероятность того, что кандидат и в самом деле "свой" (то есть собирается хранить верность группировке). Ну скажем, 0.2 - чтобы найти толкового работника, нужно несколько человек перебрать, может быть и с верными так же. Пусть эта априорная вероятность будет одинакова для людей "с улицы" и "из хорошей семьи" (такое например может быть, если "верность" определяется случайной комбинацией генов, а не полученным воспитанием); поблажку тут делать не будем (кому интересно сделать, будет возможность скачать Excel-файл и самим поэкспериментировать).
Еще немного, и мы сможем все посчитать. Остался последний этап: а какова для самого кандидата вероятность выполнить ответственное задание? Какая-то часть успеха зависит от "верности", какая-то - от личных связей кандидата, но в реальной жизни основную роль все же играет случай. Тут подчиненные схалтурили, там конкуренты подсуетились - вроде бы все делал правильно, а сидим у разбитого корыта. Предположим, что вероятность успеха все же вдвое больше, чем неудачи - 0.66. Вот теперь все численные данные готовы, подставляем их в формулу Байеса:
P(верен <- успех) = P(успех, если верен)*P(априорно верен) / ( P(успех, если верен)*P(априорно верен) + P(успех, если хитрый)*P(априорно не верен) )
- и считаем, на какой по счету проверке наши кандидаты достигнут уровня доверия в 0.95, и какова будет их вероятность этого уровня достигнуть:
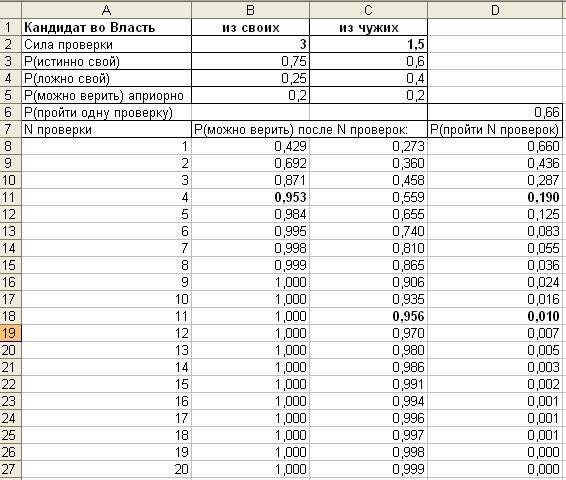
Как видите, "для своих" серия проверок работает именно так, как и планировал представитель группировки: отсеивает 4 из 5 кандидатов (вероятность успеха - 0.19). А вот "для чужих" незначительное (0.6:0.4 против 0.75:0.25) снижение доверия к результатам проверки (чужих ведь нужно проверять основательнее, чем своих) оборачивается полной безнадегой: отсеиваются 99 из 100 кандидатов. Отсеиваются, потерпев неудачу на очередном тесте - просто потому, что для них этих тестов слишком много.
Если кому-то покажется, что 1 шанс из 100 - это очень здорово, спустимся на землю. Проверка подобного рода - проект длительностью от 3 месяцев до 3 лет. Неудача в нем - серьезные денежные убытки (из чужих денег, то есть с потерей Вашей репутации, а не самих денег), а в случае особого невезения - уголовное дело. В итоге у Вас имеется прекрасная возможность потратить несколько лет жизни с 99% вероятностью испортить себе эту самую жизнь.
Но разумеется, 1% вероятность у Вас все-таки есть. Если за эти 6-7 лет на Ваше вакантное место не найдется кандидат из "своих" :)
P.S. Ознакомиться с теоремой Байеса "для любознательных" по-прежнему можно здесь. Взять экселовский файл для самостоятельных упражнений можно вот тут.
Основной массе населения вход туда заказан, один шанс из ста - это не свободный вход, а отсутствие шанса вообще (о шансах - отдельный пост). Вот об этом я и пишу: если Вы не феодал, у Вас есть шанс. Но его все равно что нет.
Так вот, ниже я хочу пояснить, что значит "есть шанс, но его все равно что нет".
Предположим, что для кооптации во властную группировку уровня N кандидату X требуется достигнуть некоторого градуса доверия со стороны группировки: "скорее не сдаст, чем сдаст". Ну скажем, вероятность 0.95, что не сдаст (меньше нельзя, "это политика, тут и убить могут").
Уверенность, сдаст или нет, можно получить, давая кандидату какие-то полномочия и наблюдая результат (были ли утечки информации или денег, не согласованные с начальством решения и т.д. и т.п). Однако насколько достоверно можно наблюдать этот результат? Ведь если ситуация "все нормально" может быть связана как с тем, что кандидат и в самом деле все сделал правильно, так и с тем, что он просто ловко замел следы. И наоборот, ситуация "что-то не то" может возникнуть и когда в самом деле не то, и когда кандидата тупо подставили (что во властной среде правило, а не исключение). Кроме того, в стремлении втереться в доверие кандидат может какое-то время воздерживаться от предательства, в надежде сорвать крупный куш (в этом смысле "все нормально" даже более подозрительно, чем "что-то не то"). Таким образом, один раз "все нормально" не сильно прибавляет доверия кандидату - "было бы ненормально, вообще убили бы". Насколько "не сильно"?
В терминах теоремы Байеса, "силой" проверки является степень правдоподобия теста - отношение вероятности истинноположительного результата (проверку прошел, потому что верный) к вероятности ложноположительного результата (проверку прошел, потому что хитрый). Первая должна быть чуть больше, чем вторая (иначе проверка ничего не дает); насколько выше? Например, в 1.5 раза (0.6:0.4) для среднего человека - то есть из десяти человек, прошедших тест, шестеро сделали это из верности, а четверо - из хитрости. А если человек не средний, а из хорошей семьи? Такому хочется сделать поблажку ("наверное должен понимать, что верным (до определенного предела) быть выгоднее, чем хитрым") - поэтому тут соотношение будет побольше, допустим, 3 раза (0.75:0.25). Я говорю сейчас о субъективной оценке вероятностей тем представителем группировки, который "ведет" данного кандидата и потом в случае чего отвечает за его верность; объективно все кандидаты могут быть верными или жуликами, для дальнейших расчетов это несущественно.
Зададим далее априорную вероятность того, что кандидат и в самом деле "свой" (то есть собирается хранить верность группировке). Ну скажем, 0.2 - чтобы найти толкового работника, нужно несколько человек перебрать, может быть и с верными так же. Пусть эта априорная вероятность будет одинакова для людей "с улицы" и "из хорошей семьи" (такое например может быть, если "верность" определяется случайной комбинацией генов, а не полученным воспитанием); поблажку тут делать не будем (кому интересно сделать, будет возможность скачать Excel-файл и самим поэкспериментировать).
Еще немного, и мы сможем все посчитать. Остался последний этап: а какова для самого кандидата вероятность выполнить ответственное задание? Какая-то часть успеха зависит от "верности", какая-то - от личных связей кандидата, но в реальной жизни основную роль все же играет случай. Тут подчиненные схалтурили, там конкуренты подсуетились - вроде бы все делал правильно, а сидим у разбитого корыта. Предположим, что вероятность успеха все же вдвое больше, чем неудачи - 0.66. Вот теперь все численные данные готовы, подставляем их в формулу Байеса:
P(верен <- успех) = P(успех, если верен)*P(априорно верен) / ( P(успех, если верен)*P(априорно верен) + P(успех, если хитрый)*P(априорно не верен) )
- и считаем, на какой по счету проверке наши кандидаты достигнут уровня доверия в 0.95, и какова будет их вероятность этого уровня достигнуть:

Как видите, "для своих" серия проверок работает именно так, как и планировал представитель группировки: отсеивает 4 из 5 кандидатов (вероятность успеха - 0.19). А вот "для чужих" незначительное (0.6:0.4 против 0.75:0.25) снижение доверия к результатам проверки (чужих ведь нужно проверять основательнее, чем своих) оборачивается полной безнадегой: отсеиваются 99 из 100 кандидатов. Отсеиваются, потерпев неудачу на очередном тесте - просто потому, что для них этих тестов слишком много.
Если кому-то покажется, что 1 шанс из 100 - это очень здорово, спустимся на землю. Проверка подобного рода - проект длительностью от 3 месяцев до 3 лет. Неудача в нем - серьезные денежные убытки (из чужих денег, то есть с потерей Вашей репутации, а не самих денег), а в случае особого невезения - уголовное дело. В итоге у Вас имеется прекрасная возможность потратить несколько лет жизни с 99% вероятностью испортить себе эту самую жизнь.
Но разумеется, 1% вероятность у Вас все-таки есть. Если за эти 6-7 лет на Ваше вакантное место не найдется кандидат из "своих" :)
P.S. Ознакомиться с теоремой Байеса "для любознательных" по-прежнему можно здесь. Взять экселовский файл для самостоятельных упражнений можно вот тут.