Квантовый ликбез 25-5. Алгоритм Гровера - повторение и измерение
Предыдущие посты
Здесь мы немного уточним и дополним то, что уже говорилось в общем обзоре алгоритма Гровера. А также поговорим о том, почему квантовые компьютеры до сих пор не окружают нас со всех сторон.
После первого прохода алгоритма, на выходе блока 3, мы получили некоторое усиление "правильного" значения, точнее, увеличение амплитуды вероятности соответсвующей альтернативы. Но "некоторое" нас не устраивает, нам нужно макимально повысить вероятность получения результата. для этого мы повторим действия оракула и усилителя определённое количество раз. В каждом проходе оракул будет изменять знак амплитуды вероятности "правильной" альтернативы с положительного на отрицательный. А усилитель будет увеличивать по модулю "отрицательную" амплитуду вероятности.
В примере после первого прохода у нас следующий расклад:
- амплитуды вероятности "неправильных" альтернатив: +0,1875
- амплитуда вероятности "правильной" альтернативы: +0,6875
После второго прохода:
- амплитуды вероятности "неправильных" альтернатив: +0,078*
- амплитуда вероятности "правильной" альтернативы: +0,953
* Здесь и ниже округлегно до трёх знаков после запятой.
После третьего прохода:
- амплитуды вероятности "неправильных" альтернатив: -0,051
- амплитуда вероятности "правильной" альтернативы: -0,980
Всё, для нашей задачи мы достигли возможного максимума усиления. Убедитесь сами, что если мы сделаем ещё один проход блоков 2 и 3, то получим:
- амплитуды вероятности "неправильных" альтернатив: -0,167
- амплитуда вероятности "правильной" альтернативы: +0,763
То есть, "правильная" амплитуда вероятности после четвёртого прохода уменьшится.
Короче, нужно вовремя остановится. В общем обзоре уже говорилось, что наибольшее усиление достигается после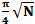
проходов, с округлением до меньшего целого. Но, внимание, это верно для тех задач поиска, где среди всего множества проверяемых значений имеется только одно правильное. Если же значений, удовлятворяющих критерию поиска два или больше, количество проходов блоков 2 и 3 должно быть уменьшено. Так что желательно заранее знать, сколько у нас правильных значений среди проверяемого множества. Это, безусловно, недостаток алгоритма Гровера, но не очень страшный.
Итак, после некоторого количества проходов блоков 2 и 3, мы достигаем максимально возможного усиления "правильных" альтернатив. Остаётся только "прочитать" результат. Для этого мы измеряем все кубиты подрегистра данных. По-очереди или одновременно - это не существенно. Важно зафиксировать результаты измерений и получить готовый ответ в форме двоичного числа 〈xk〉...〈x1〉. Напомню, что в двух угловых скобках мы показывем результат измерения.
На вычислительных схемах неунитарную операцию измерения будем обозначать вот таким символом:
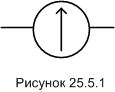
В примере мы с вероятностью примерно 0,961 получим при измерении правильныый ответ: двоичное число 〈1〉〈0〉〈0〉〈1〉.
Поскольку всё же существует небольшая вероятность того, что результат будет неправильным, нам следует проверить полученное значение "вручную" или на классическом компьютере. Если всё сошлось - прекрасно, расчёт окончен, результат получен. Если нет - значит, на первый раз не повезло. Не страшно, мы просто проделаем наши квантовые вычисления снова. Имеется в виду - полностью, начиная от инициализации и с необходимым количеством повторов блоков 2 и 3.
В примере вероятность неудачи составляет около 0,04 - это довольно много. Но у нас в подрегистре данных было всего 4 кубита - "игрушечная" задача. А вообще, чем больше подрегистр данных, тем меньше вероятность ошибки. Для задач, в которых проверяемое множество из N чисел содержит только одно правильное значение, вероятность ошибки составит примерно:
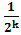
.
Просто для демонстрации: если в подрегистре данных полсотни кубитов, тогда вероятность ошибки составит около одной квадриллионной. При таком раскладе, чтобы получить неправильный результат, надо быть очень, очень невезучим!
Для задач, где правильных решений несколько, вероятность ошибки будет величиной того же порядка, то есть, очень маленькой. При условии, конечно, что мы сделаем оптимальное количество проходов блоков 2 и 3.
Мы тут по ходу дела разбирали "учебный" 4-х кубитный пример и рисовали отдельные кусочки вычислительной схемы. Давайте теперь изобразим эту схему целиком на одной картинке.
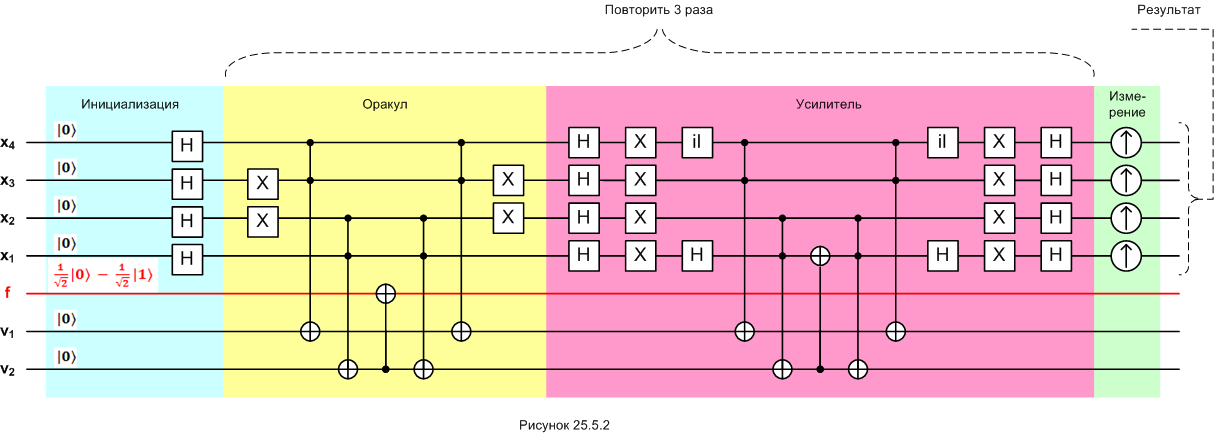
В завершение рассказа об алгоритме Гровера следует ещё раз сказать о следующем. Мы берём систему из нескольких кубитов и приводим её в исходное квантовое состояние. Затем мы оказываем на эту систему ряд воздействий, тем самым заставляя наш квантовый компьютер выполнять заданную программу. При этом квантовое состояние системы меняется строго определённым образом, тут нет места никаким случайностям (возможные сбои оборудования и ошибки оператора оставляем за скобками). В таком разрезе неправильно думать, что квантовое вычисление имеет вероятностный характер: до считывания результата - измерения - квантовая эволюция нашей системы кубитов однозначно детерминирова. Случайность "играет" только при измерении. Но алгоритм Гровера сводит роль случая к мимнимуму, вероятность получить неверный ответ очень невелика.
Тут вы можете спросить: почему же эти замечательные квантовые компьютеры существуют пока только в виде теоретических моделей, типа той, что мы тут изучали, и в виде примитивных экспериментальных образцов? Ответ прост: всё дело в технических трудностях.
Тут ведь что требуется? Во-первых, нужна стабильность кубитов. То есть, они должны сохранять своё квантовое состояние неизменным, пока нам не потребуется целенаправленно его изменить по ходу выполнения алгоритма. Но обеспечить такую стабильность очень трудно: ведь кубит сохраняет стационарное квантовое состояние только в отсутсвии внешних воздействий. Изобретено уже довольно много квантовых систем, потенциально годящихся на роль кубитов, но ни одна из них не обеспечивает требуемой стабильности, не удаётся пока должным образом изолировать кубит от окружающей среды.
Во-вторых, есть трудности с реализацией квантовых операций - гейтов. Необходимо научиться очень точно управлять квантовыми состояниями кубитов. С одиночными гейтами - однокубитными операциями - дело обстоит более-менее нормально. Но надёжных технологий реалихзации двух- и более кубитных операций пока ещё нет.
Но, повторяю, это трудности инженерно-технические, никаких теоретических препятсвий к созданию квантовых компьютеров нет. Так что в скором будущем ждите больших перемен!
Окончание
Здесь мы немного уточним и дополним то, что уже говорилось в общем обзоре алгоритма Гровера. А также поговорим о том, почему квантовые компьютеры до сих пор не окружают нас со всех сторон.
После первого прохода алгоритма, на выходе блока 3, мы получили некоторое усиление "правильного" значения, точнее, увеличение амплитуды вероятности соответсвующей альтернативы. Но "некоторое" нас не устраивает, нам нужно макимально повысить вероятность получения результата. для этого мы повторим действия оракула и усилителя определённое количество раз. В каждом проходе оракул будет изменять знак амплитуды вероятности "правильной" альтернативы с положительного на отрицательный. А усилитель будет увеличивать по модулю "отрицательную" амплитуду вероятности.
В примере после первого прохода у нас следующий расклад:
- амплитуды вероятности "неправильных" альтернатив: +0,1875
- амплитуда вероятности "правильной" альтернативы: +0,6875
После второго прохода:
- амплитуды вероятности "неправильных" альтернатив: +0,078*
- амплитуда вероятности "правильной" альтернативы: +0,953
* Здесь и ниже округлегно до трёх знаков после запятой.
После третьего прохода:
- амплитуды вероятности "неправильных" альтернатив: -0,051
- амплитуда вероятности "правильной" альтернативы: -0,980
Всё, для нашей задачи мы достигли возможного максимума усиления. Убедитесь сами, что если мы сделаем ещё один проход блоков 2 и 3, то получим:
- амплитуды вероятности "неправильных" альтернатив: -0,167
- амплитуда вероятности "правильной" альтернативы: +0,763
То есть, "правильная" амплитуда вероятности после четвёртого прохода уменьшится.
Короче, нужно вовремя остановится. В общем обзоре уже говорилось, что наибольшее усиление достигается после
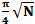
проходов, с округлением до меньшего целого. Но, внимание, это верно для тех задач поиска, где среди всего множества проверяемых значений имеется только одно правильное. Если же значений, удовлятворяющих критерию поиска два или больше, количество проходов блоков 2 и 3 должно быть уменьшено. Так что желательно заранее знать, сколько у нас правильных значений среди проверяемого множества. Это, безусловно, недостаток алгоритма Гровера, но не очень страшный.
Итак, после некоторого количества проходов блоков 2 и 3, мы достигаем максимально возможного усиления "правильных" альтернатив. Остаётся только "прочитать" результат. Для этого мы измеряем все кубиты подрегистра данных. По-очереди или одновременно - это не существенно. Важно зафиксировать результаты измерений и получить готовый ответ в форме двоичного числа 〈xk〉...〈x1〉. Напомню, что в двух угловых скобках мы показывем результат измерения.
На вычислительных схемах неунитарную операцию измерения будем обозначать вот таким символом:

В примере мы с вероятностью примерно 0,961 получим при измерении правильныый ответ: двоичное число 〈1〉〈0〉〈0〉〈1〉.
Поскольку всё же существует небольшая вероятность того, что результат будет неправильным, нам следует проверить полученное значение "вручную" или на классическом компьютере. Если всё сошлось - прекрасно, расчёт окончен, результат получен. Если нет - значит, на первый раз не повезло. Не страшно, мы просто проделаем наши квантовые вычисления снова. Имеется в виду - полностью, начиная от инициализации и с необходимым количеством повторов блоков 2 и 3.
В примере вероятность неудачи составляет около 0,04 - это довольно много. Но у нас в подрегистре данных было всего 4 кубита - "игрушечная" задача. А вообще, чем больше подрегистр данных, тем меньше вероятность ошибки. Для задач, в которых проверяемое множество из N чисел содержит только одно правильное значение, вероятность ошибки составит примерно:
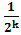
.
Просто для демонстрации: если в подрегистре данных полсотни кубитов, тогда вероятность ошибки составит около одной квадриллионной. При таком раскладе, чтобы получить неправильный результат, надо быть очень, очень невезучим!
Для задач, где правильных решений несколько, вероятность ошибки будет величиной того же порядка, то есть, очень маленькой. При условии, конечно, что мы сделаем оптимальное количество проходов блоков 2 и 3.
Мы тут по ходу дела разбирали "учебный" 4-х кубитный пример и рисовали отдельные кусочки вычислительной схемы. Давайте теперь изобразим эту схему целиком на одной картинке.

В завершение рассказа об алгоритме Гровера следует ещё раз сказать о следующем. Мы берём систему из нескольких кубитов и приводим её в исходное квантовое состояние. Затем мы оказываем на эту систему ряд воздействий, тем самым заставляя наш квантовый компьютер выполнять заданную программу. При этом квантовое состояние системы меняется строго определённым образом, тут нет места никаким случайностям (возможные сбои оборудования и ошибки оператора оставляем за скобками). В таком разрезе неправильно думать, что квантовое вычисление имеет вероятностный характер: до считывания результата - измерения - квантовая эволюция нашей системы кубитов однозначно детерминирова. Случайность "играет" только при измерении. Но алгоритм Гровера сводит роль случая к мимнимуму, вероятность получить неверный ответ очень невелика.
Тут вы можете спросить: почему же эти замечательные квантовые компьютеры существуют пока только в виде теоретических моделей, типа той, что мы тут изучали, и в виде примитивных экспериментальных образцов? Ответ прост: всё дело в технических трудностях.
Тут ведь что требуется? Во-первых, нужна стабильность кубитов. То есть, они должны сохранять своё квантовое состояние неизменным, пока нам не потребуется целенаправленно его изменить по ходу выполнения алгоритма. Но обеспечить такую стабильность очень трудно: ведь кубит сохраняет стационарное квантовое состояние только в отсутсвии внешних воздействий. Изобретено уже довольно много квантовых систем, потенциально годящихся на роль кубитов, но ни одна из них не обеспечивает требуемой стабильности, не удаётся пока должным образом изолировать кубит от окружающей среды.
Во-вторых, есть трудности с реализацией квантовых операций - гейтов. Необходимо научиться очень точно управлять квантовыми состояниями кубитов. С одиночными гейтами - однокубитными операциями - дело обстоит более-менее нормально. Но надёжных технологий реалихзации двух- и более кубитных операций пока ещё нет.
Но, повторяю, это трудности инженерно-технические, никаких теоретических препятсвий к созданию квантовых компьютеров нет. Так что в скором будущем ждите больших перемен!
Окончание