Квантовый ликбез 21-3. Квантовая телепортация - окончание
Предыдущие посты
Тут ненадолго отвлёчемся от телепортации и посмотрим подробнее, что произошло. Заодно освоим, как «работают» наши диаграммы.
До операции [CNOTFA] кубит «F» и пара «AB» не запутаны друг с другом. А вот теперь они запутались. Если Алиса сейчас измерит кубит «F», то состояние пары «AB» будет зависеть от результата этого измерения. В частности, вот что произойдёт, если при измерении кубита получится результат 〈0〉:
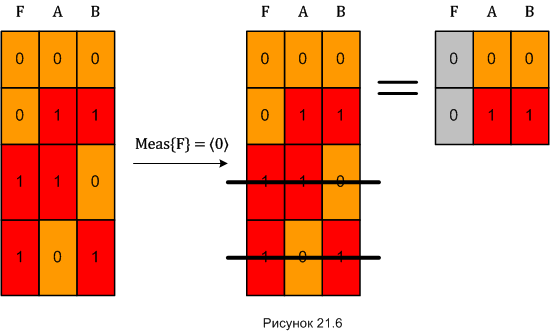
Запись вида Meas{F} = 〈0〉 будет обозначать, что мы измерили кубит «F» и получили результат 〈0〉.
В соответствии с шестым постулатом, такое измерение «вычеркивает» из числа реализуемых все трёхкубитные группы, в который результат измерения кубита «F» предопределён как 〈1〉. Это и показано на рисунке: две нижние строки из левой диаграммы вычёркиваем и получаем состояние, нарисованное справа. Кубит «F» полностью определился, это обстоятельство на диаграмме обозначено серым цветом соответствующих клеточек. Состояние пары «AB» этом случае проецируется вот в это:
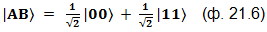
Если же при измерении кубита «F», будет получен результат 〈1〉, тогда произойдёт следующее (промежуточную картинку с вычёркиванием пропускаем):
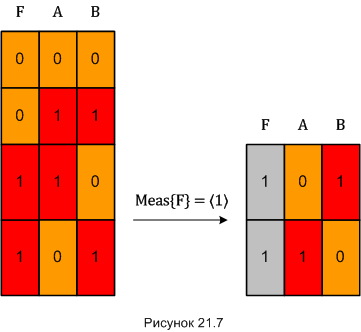
В виде формулы квантовое состояние пары «AB» выглядит теперь так:
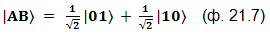
Сравните формулы (ф. 21.6) и (ф.21.7) или правые диаграммы на рисунках 21.6, 21.7: существенно разные состояния пары «AB»!
Но возвращаемся к телепортации. Итак, первым действием Алиса запутала кубит «F» с кубитами «A» и «B» и получила состояние (ф. 21.5). Дальше она подвергает кубит «F» воздействию, которое называется «операция Адамара» и обозначается как [H]. Операция Адамара расщепляет базисные состояния кубита следующим образом:
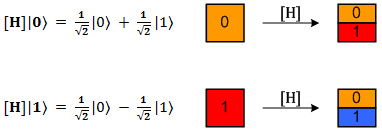
Вот нам и пригодились элементы синего цвета для обозначения групп с отрицательной амплитудой вероятности.
Применение операции [HF] к состоянию (ф. 21.5) приводит к следующему состоянию:
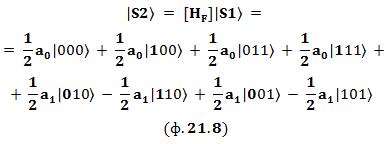
Или вот, пожалуйста, на диаграмме:
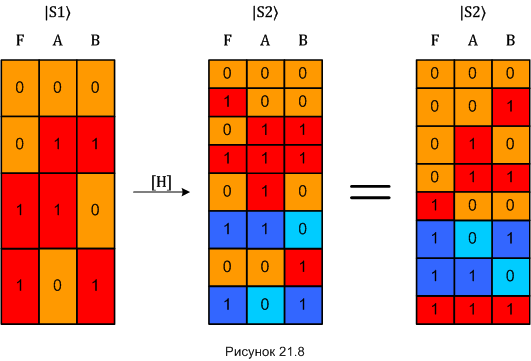
Результат операции показан на центральном рисунке. Было четыре группы. После операции каждая из них расщепилась на две, стало восемь групп.
На правом рисунке показано то же самое состояние, что и на центральном, но группы - строки упорядочены для удобства дальнейшего объяснения.
Теперь Алиса измеряет свои кубиты, сначала кубит «F», затем кубит «A». Изобразим то, что происходит с трёхкубитным состоянием при различных результатах измерений на одной большой картинке:
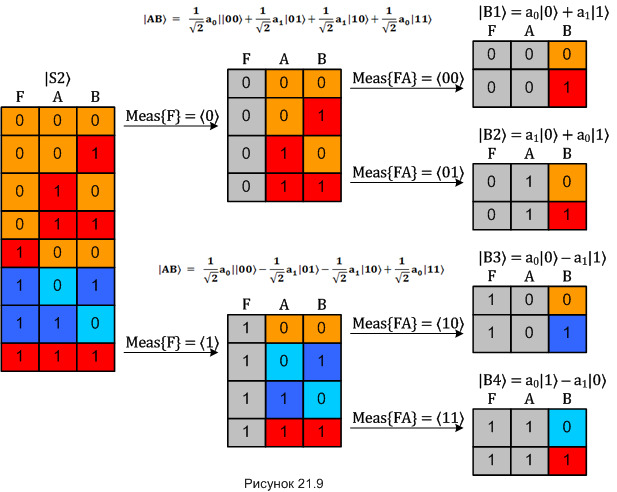
Глядя на диаграмму, видим, что после двух алисиных измерений кубит Боба - кубит «B» - может находится в одном из четырёх состояний. В каком именно - это жестко зависит от результатов, которые получила Алиса. Формулы этих четырёх состояний показаны прямо на рисунке.
Теперь Боб должен слегка «поработать» над своим кубитом. Что именно надо сделать - это Боб может узнать только после того, как получит результаты измерений от Алисы по обычному каналу связи. Четыре инструкции для Боба:
1) Если результат измерений Алисы 〈00〉, значит, кубит «B» находится в состоянии |B1〉. Но посмотрите, это состояние в точности совпадает с исходным состоянием |𝛙〉 кубита «F» (ф. 21.1). Ура! Акт телепортации состояния уже состоялся, Бобу ничего делать не надо.
2) Если результат измерений Алисы 〈01〉, значит, кубит «B» находится в состоянии |B2〉. В этом случае Боб подвергает кубит «B» унитарной операции, которая обозначается как [X]. Эта операция изменят базисные состояния кубита следующим образом:
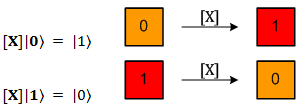
Эта операция превращает состояние |0〉 в состояние |1〉 и наоборот.
При таком воздействии на состояние |B2〉 происходит следующее:
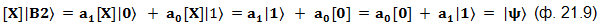
На диаграмме это выглядит так:
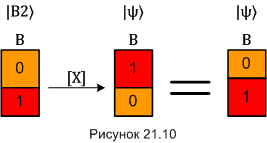
3) Если результат измерений Алисы 〈10〉, значит, кубит «B» находится в состоянии |B3〉. В этом случае Боб подвергает кубит «B» унитарной операции, которая обозначается как [Z]. Эта операция изменят базисные состояния кубита следующим образом:
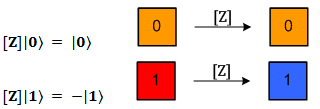
Эта операция оставляет неизменным состояние |0〉 и меняет знак состояния |1〉.
При таком воздействии на состояние |B3〉 происходит следующее:
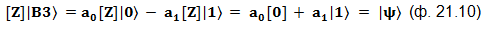
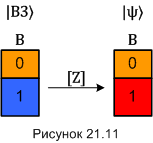
На диаграмме это выглядит так:
4) Если результат измерений Алисы 〈11〉, значит, кубит «B» находится в состоянии |B4〉. В этом случае Боб подвергает кубит «B» двум унитарным операциям: сначала [X], потом [Z].
Происходит следующее:
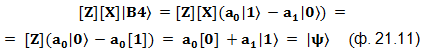
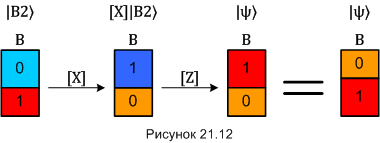
На диаграмме это выглядит так:
Итак, в любом из четырёх случаев, если Боб строго придерживается этих инструкций, кубит приходит в квантовое состояние |𝛙〉 - телепортация работает.
Ещё раз призываю вас проникнуться «волшебством» этого действа. По сути дела, квантовая телепортация заключается в передаче из кубита-источника в кубит-приёмник двух чисел: амплитуд вероятности a0 и a1. В нашем случае это были действительные числа:
a0 = 0,6
a1 = 0,8
Но в общем случае это могут быть два произвольных комплексных числа (удовлетворяющие условию нормирования). С точки зрения классической теории информации для хранения произвольного комплексного числа требуется носитель информации бесконечной ёмкости. Кубит таковым носителем и является, ведь, как мы знаем, он несёт в себе бесконечное количество виртуальных вариантов будущего.
А для перезаписи этой бесконечной информации на другой носитель требуется, по «классике», передать бесконечное количество битов. Но для осуществения квантовой телепортации нам достаточно проделать несколько локальных манипуляций и передать всего лишь два классических бита, и бесконечно разнообразная картина виртуальных вариантов, выражаемая числами a0 и a1, «волшебным» образом перемещается из источника в приёмник.
Если есть неясности по квантовой телепортации - прошу задавать вопросы. Если нет, тогда и с квантовыми вычислениями разберёмся в следующей части.
Продолжение
Тут ненадолго отвлёчемся от телепортации и посмотрим подробнее, что произошло. Заодно освоим, как «работают» наши диаграммы.
До операции [CNOTFA] кубит «F» и пара «AB» не запутаны друг с другом. А вот теперь они запутались. Если Алиса сейчас измерит кубит «F», то состояние пары «AB» будет зависеть от результата этого измерения. В частности, вот что произойдёт, если при измерении кубита получится результат 〈0〉:

Запись вида Meas{F} = 〈0〉 будет обозначать, что мы измерили кубит «F» и получили результат 〈0〉.
В соответствии с шестым постулатом, такое измерение «вычеркивает» из числа реализуемых все трёхкубитные группы, в который результат измерения кубита «F» предопределён как 〈1〉. Это и показано на рисунке: две нижние строки из левой диаграммы вычёркиваем и получаем состояние, нарисованное справа. Кубит «F» полностью определился, это обстоятельство на диаграмме обозначено серым цветом соответствующих клеточек. Состояние пары «AB» этом случае проецируется вот в это:
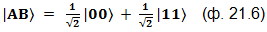
Если же при измерении кубита «F», будет получен результат 〈1〉, тогда произойдёт следующее (промежуточную картинку с вычёркиванием пропускаем):

В виде формулы квантовое состояние пары «AB» выглядит теперь так:
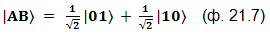
Сравните формулы (ф. 21.6) и (ф.21.7) или правые диаграммы на рисунках 21.6, 21.7: существенно разные состояния пары «AB»!
Но возвращаемся к телепортации. Итак, первым действием Алиса запутала кубит «F» с кубитами «A» и «B» и получила состояние (ф. 21.5). Дальше она подвергает кубит «F» воздействию, которое называется «операция Адамара» и обозначается как [H]. Операция Адамара расщепляет базисные состояния кубита следующим образом:
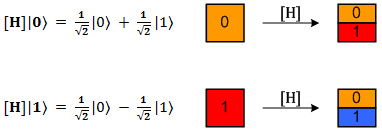
Вот нам и пригодились элементы синего цвета для обозначения групп с отрицательной амплитудой вероятности.
Применение операции [HF] к состоянию (ф. 21.5) приводит к следующему состоянию:
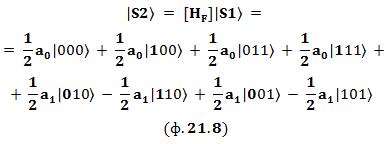
Или вот, пожалуйста, на диаграмме:

Результат операции показан на центральном рисунке. Было четыре группы. После операции каждая из них расщепилась на две, стало восемь групп.
На правом рисунке показано то же самое состояние, что и на центральном, но группы - строки упорядочены для удобства дальнейшего объяснения.
Теперь Алиса измеряет свои кубиты, сначала кубит «F», затем кубит «A». Изобразим то, что происходит с трёхкубитным состоянием при различных результатах измерений на одной большой картинке:

Глядя на диаграмму, видим, что после двух алисиных измерений кубит Боба - кубит «B» - может находится в одном из четырёх состояний. В каком именно - это жестко зависит от результатов, которые получила Алиса. Формулы этих четырёх состояний показаны прямо на рисунке.
Теперь Боб должен слегка «поработать» над своим кубитом. Что именно надо сделать - это Боб может узнать только после того, как получит результаты измерений от Алисы по обычному каналу связи. Четыре инструкции для Боба:
1) Если результат измерений Алисы 〈00〉, значит, кубит «B» находится в состоянии |B1〉. Но посмотрите, это состояние в точности совпадает с исходным состоянием |𝛙〉 кубита «F» (ф. 21.1). Ура! Акт телепортации состояния уже состоялся, Бобу ничего делать не надо.
2) Если результат измерений Алисы 〈01〉, значит, кубит «B» находится в состоянии |B2〉. В этом случае Боб подвергает кубит «B» унитарной операции, которая обозначается как [X]. Эта операция изменят базисные состояния кубита следующим образом:

Эта операция превращает состояние |0〉 в состояние |1〉 и наоборот.
При таком воздействии на состояние |B2〉 происходит следующее:
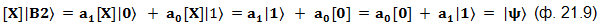
На диаграмме это выглядит так:

3) Если результат измерений Алисы 〈10〉, значит, кубит «B» находится в состоянии |B3〉. В этом случае Боб подвергает кубит «B» унитарной операции, которая обозначается как [Z]. Эта операция изменят базисные состояния кубита следующим образом:

Эта операция оставляет неизменным состояние |0〉 и меняет знак состояния |1〉.
При таком воздействии на состояние |B3〉 происходит следующее:
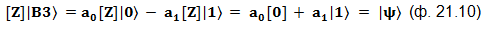
На диаграмме это выглядит так:

4) Если результат измерений Алисы 〈11〉, значит, кубит «B» находится в состоянии |B4〉. В этом случае Боб подвергает кубит «B» двум унитарным операциям: сначала [X], потом [Z].
Происходит следующее:
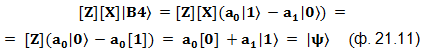
На диаграмме это выглядит так:

Итак, в любом из четырёх случаев, если Боб строго придерживается этих инструкций, кубит приходит в квантовое состояние |𝛙〉 - телепортация работает.
Ещё раз призываю вас проникнуться «волшебством» этого действа. По сути дела, квантовая телепортация заключается в передаче из кубита-источника в кубит-приёмник двух чисел: амплитуд вероятности a0 и a1. В нашем случае это были действительные числа:
a0 = 0,6
a1 = 0,8
Но в общем случае это могут быть два произвольных комплексных числа (удовлетворяющие условию нормирования). С точки зрения классической теории информации для хранения произвольного комплексного числа требуется носитель информации бесконечной ёмкости. Кубит таковым носителем и является, ведь, как мы знаем, он несёт в себе бесконечное количество виртуальных вариантов будущего.
А для перезаписи этой бесконечной информации на другой носитель требуется, по «классике», передать бесконечное количество битов. Но для осуществения квантовой телепортации нам достаточно проделать несколько локальных манипуляций и передать всего лишь два классических бита, и бесконечно разнообразная картина виртуальных вариантов, выражаемая числами a0 и a1, «волшебным» образом перемещается из источника в приёмник.
Если есть неясности по квантовой телепортации - прошу задавать вопросы. Если нет, тогда и с квантовыми вычислениями разберёмся в следующей части.
Продолжение