Квантовый ликбез - 18-2. Квантовое видение в темноте
Предыдущие посты
Конфуций утверждал, что невозможно, мол, увидеть чёрную кошку в тёмной комнате и ошибался, потому что не знал квантовой механики. На самом деле можно, при условии, конечно, что кошка там есть. Иными словами, законы квантовой механики позволяют увидеть предмет в полной темноте, то есть, не осветив его ни единым фотоном. И вообще никак на него в классическом смысле не воздействуя.
Давайте вспомним эксперимент, который мы проводили в шестой части и изобразим его ещё раз на рисунке 18.2.1.
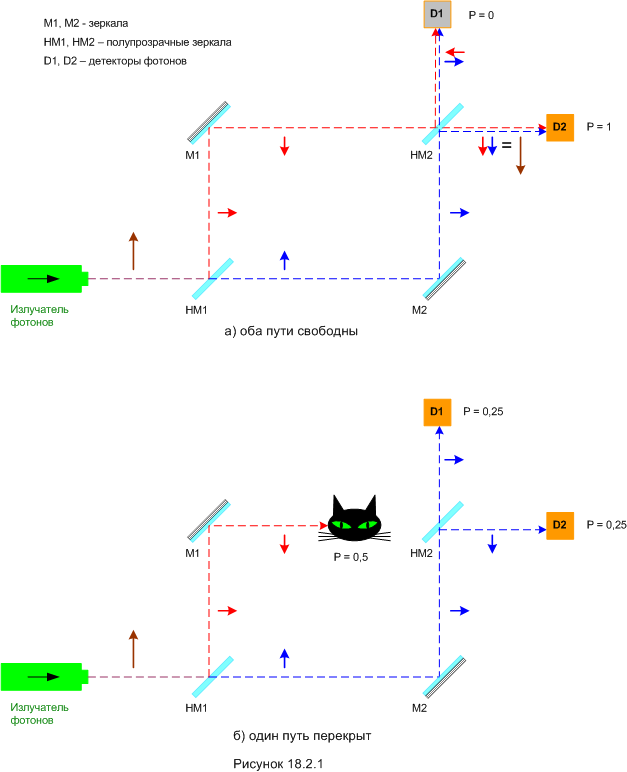
Имеется излучатель одиночных фотонов, два детектора и система зеркал, обеспечивающая два альтернативных, одинаковых по длине пути фотона от излучателя к детекторам. В случае, если оба пути открыты, фотон может попасть только в детектор D2. Почему это происходит - в общих чертах уже объяснялось в шестой части, теперь у нас есть более точное объяснение.
Частица, свободно летящая в пространстве, представляет собой на самом деле вытянутое облако реализуемых виртуальных вариантов. Вектор амплитуды вероятности вдоль этого облака циклически меняется по направлению, образуя подобие волны. На полупрозрачном зеркале это облако разделяется надвое. Причём, в том «полуоблаке», которое «отражается» от зеркала, происходит сдвиг по фазе на четверть волны. Или, что то же самое, проворот всех векторов амплитуд вероятности на четверть оборота в их условном пространстве. А в том, которое проходит зеркало насквозь, никакого сдвига фазы нет. Вот как-то так:

Цветовая кодировка, как вы помните по предыдущему выпуску ликбеза, обозначает направление вектора амплитуды вероятности в данной точке пространства.
Если оба пути открыты (случай «а» на рисунке 18.2.1), полупрозрачного зеркала HM2 достигают два полуоблака, условно - верхнее и нижнее. Зеркало HM2 опять «открывает» два альтернативных пути для каждого из них. На пути к D1 совмещаются виртуальные «четвертинки» облаков, испытавшие первая (прошедшее верхним путём) - три отражения и три четвертьволновых сдвига, вторая (прошедшее нижним путём) - одно отражение. Стало быть, вектора амплитуд вероятности этих двух четвертинок сдвинуты друг относительно друга на пол-оборота, и вступая в деструктивную интерференцию, «гасят» друг друга. Таким образом, если оба пути открыты, вероятность фотона попасть в D1 равняется нулю. А на пути к D2 обе четвертинки прошли через два отражения. Следовательно, никакого сдвига по фазе между ними нет, происходит конструктивная интерференция. Вероятность попасть в D2 равна единице.
Если один из путей закрыт, (случай «б» на рисунке 18.2.1), тогда зеркала HM2 достигает только одно полуоблако, другое поглощается преградой. Обе четвертинки "выжившего" полуоблака после зеркала HM2 на путях к D1 и D2 никакой деструктивной интерференции не подвергаются, так что с равной вероятностью может сработать любой из детекторов.
Иногда говорят ещё, что в случае, если оба пути открыты, частица демонстрирует волновое поведение - интерферирует (сама с собой?). А в случае, если есть только один путь, частица демонстрирует корпускулярное поведение - ведёт себя как маленький шарик.
Давайте теперь посмотрим на этот опыт с другой точки зрения. Допустим, мы, начиная эксперимент, не знаем, есть ли на одном из путей препятствие, но хотим это узнать. Вот мы выпускаем одиночный фотон, дальше возможны три результата.
1. Срабатывает D2. Этот результат нам ничего не говорит, он возможен как при наличии, так и при отсутствии препятствия.
2. Не срабатывает ни один детектор. Теперь очевидно, что препятствие есть и фотон разбился об него. Но это тривиальный классический случай.
3. Срабатывает детектор D1. Тоже понятно, что препятствие есть. Но, обратите внимание: мы обнаружили препятствие, не оказав при этом на него ни малейшего воздействия, ни один реальный фотон в него не попал. Мы буквально «увидели черную кошку в тёмной комнате».
Вот так на самом деле устроен мир. Если с классической точки зрения невозможно наблюдать предметы, никак с ними не взаимодействуя, то квантовая механика такую возможность даёт. Здесь мы рассмотрели самый простой пример «квантового видения в темноте». Тем, кто желает разобраться с этим «чудом» поглубже, рекомендую вот эту статью.
А в следующем посте мы поборемся с антиквантовой конспирологией и поговорим об экспериментах с отложенным выбором.
Продолжение
Конфуций утверждал, что невозможно, мол, увидеть чёрную кошку в тёмной комнате и ошибался, потому что не знал квантовой механики. На самом деле можно, при условии, конечно, что кошка там есть. Иными словами, законы квантовой механики позволяют увидеть предмет в полной темноте, то есть, не осветив его ни единым фотоном. И вообще никак на него в классическом смысле не воздействуя.
Давайте вспомним эксперимент, который мы проводили в шестой части и изобразим его ещё раз на рисунке 18.2.1.

Имеется излучатель одиночных фотонов, два детектора и система зеркал, обеспечивающая два альтернативных, одинаковых по длине пути фотона от излучателя к детекторам. В случае, если оба пути открыты, фотон может попасть только в детектор D2. Почему это происходит - в общих чертах уже объяснялось в шестой части, теперь у нас есть более точное объяснение.
Частица, свободно летящая в пространстве, представляет собой на самом деле вытянутое облако реализуемых виртуальных вариантов. Вектор амплитуды вероятности вдоль этого облака циклически меняется по направлению, образуя подобие волны. На полупрозрачном зеркале это облако разделяется надвое. Причём, в том «полуоблаке», которое «отражается» от зеркала, происходит сдвиг по фазе на четверть волны. Или, что то же самое, проворот всех векторов амплитуд вероятности на четверть оборота в их условном пространстве. А в том, которое проходит зеркало насквозь, никакого сдвига фазы нет. Вот как-то так:

Цветовая кодировка, как вы помните по предыдущему выпуску ликбеза, обозначает направление вектора амплитуды вероятности в данной точке пространства.
Если оба пути открыты (случай «а» на рисунке 18.2.1), полупрозрачного зеркала HM2 достигают два полуоблака, условно - верхнее и нижнее. Зеркало HM2 опять «открывает» два альтернативных пути для каждого из них. На пути к D1 совмещаются виртуальные «четвертинки» облаков, испытавшие первая (прошедшее верхним путём) - три отражения и три четвертьволновых сдвига, вторая (прошедшее нижним путём) - одно отражение. Стало быть, вектора амплитуд вероятности этих двух четвертинок сдвинуты друг относительно друга на пол-оборота, и вступая в деструктивную интерференцию, «гасят» друг друга. Таким образом, если оба пути открыты, вероятность фотона попасть в D1 равняется нулю. А на пути к D2 обе четвертинки прошли через два отражения. Следовательно, никакого сдвига по фазе между ними нет, происходит конструктивная интерференция. Вероятность попасть в D2 равна единице.
Если один из путей закрыт, (случай «б» на рисунке 18.2.1), тогда зеркала HM2 достигает только одно полуоблако, другое поглощается преградой. Обе четвертинки "выжившего" полуоблака после зеркала HM2 на путях к D1 и D2 никакой деструктивной интерференции не подвергаются, так что с равной вероятностью может сработать любой из детекторов.
Иногда говорят ещё, что в случае, если оба пути открыты, частица демонстрирует волновое поведение - интерферирует (сама с собой?). А в случае, если есть только один путь, частица демонстрирует корпускулярное поведение - ведёт себя как маленький шарик.
Давайте теперь посмотрим на этот опыт с другой точки зрения. Допустим, мы, начиная эксперимент, не знаем, есть ли на одном из путей препятствие, но хотим это узнать. Вот мы выпускаем одиночный фотон, дальше возможны три результата.
1. Срабатывает D2. Этот результат нам ничего не говорит, он возможен как при наличии, так и при отсутствии препятствия.
2. Не срабатывает ни один детектор. Теперь очевидно, что препятствие есть и фотон разбился об него. Но это тривиальный классический случай.
3. Срабатывает детектор D1. Тоже понятно, что препятствие есть. Но, обратите внимание: мы обнаружили препятствие, не оказав при этом на него ни малейшего воздействия, ни один реальный фотон в него не попал. Мы буквально «увидели черную кошку в тёмной комнате».
Вот так на самом деле устроен мир. Если с классической точки зрения невозможно наблюдать предметы, никак с ними не взаимодействуя, то квантовая механика такую возможность даёт. Здесь мы рассмотрели самый простой пример «квантового видения в темноте». Тем, кто желает разобраться с этим «чудом» поглубже, рекомендую вот эту статью.
А в следующем посте мы поборемся с антиквантовой конспирологией и поговорим об экспериментах с отложенным выбором.
Продолжение