Модель выборов. Распределение вброса
Первый и второй предыдущие посты, посвящённые проблеме интерпретации результатов выборов, дают наглядное представление о виде перехода от исходной гауссовой кривой к реальной, составленной по официальным данным ЦИК, но ничего не говорят о возможном механизме такого перехода.
Попробуем подробнее разобраться в этом вопросе. Сделаем это на примере голосования в Москве. Распределение голосов здесь имело интересную изломанную двугорбую форму:

Здесь горизонтальная ось является осью явки (от числа зарегистрированных на избирательном участке). По вертикальной оси отложен % голосов избирателей, суммированных по участкам, попавшим в +-0,5% интервал оси явки, т.е. это гистограмма глобальной явки, изображённая в виде графика (всего под кривой 100%).
По поводу возможных причин двугорбости (и того, что эта двугорбость начала проявляться уже в промежуточных отчётах УИК об явке) сломано много копий в посте популяризатора распределений явки oude_rus: Дива -- не прочесть тайну. Рассматривалось множество версий, приводились гипотезы о разной активности избирателей в разных округах Москвы, о разных типах избирателей (вроде мужчин и женщин), о волшебстве Чурова, о разных типах председателей УИК, но к однозначному мнению не пришли.
Посмотрим, как можно прийти к двугорбости, оперируя цифрами различия фальсификаций на разных участках.
Для начала зададимся возможными характеристиками исходного гауссового распределения явки. Оно характеризуется всего лишь двумя характеристиками - средним значением и СКО - среднеквадратическим отклонением.
Среднюю величину вброса 14,35% дает podmoskovnik в своей статье "Математика выборов - 2011" в газете "Троицкий вариант". СКО исходного распределения его методом вычислить нельзя, но из консультаций было уточнено, что оно может находиться в диапазоне 3,4-4,2%.
Примем среднее значение равным 47% (соответствует вбросу 14,3%) со СКО = 4% (по оси явки). Исходная и получившиеся кривые тогда будут такими (площадь под гауссовой кривой - 100%, под кривой показанной явки увеличена соответственно предполагаемому вбросу):
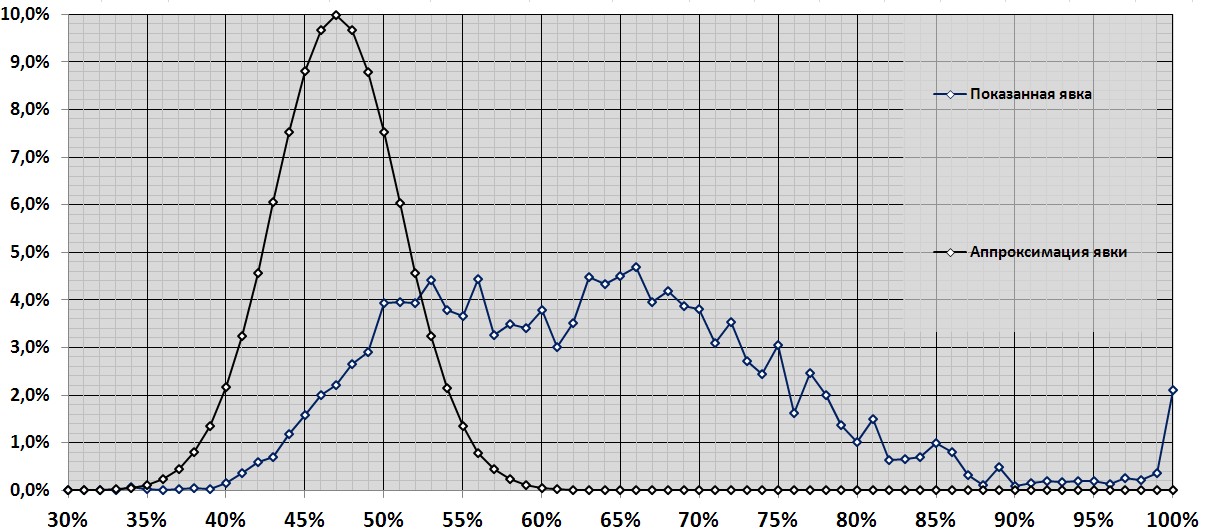
Каким образом из одной кривой получается другая и как влияет вброс на кривую распределения явки? Поскольку вброшенные бюллетени не существуют сами по себе, а складываются с уже имеющимися на участке, процент явки на этом участке увеличивается на процент вброшенных бюллетеней. Например, если исходный процент явки был 47%, а дополнительно вброшено (любым образом, скажем, добавлено при вводе данных в систему ГАС "Выборы") 19% бюллетеней (от зарегистрированного количества избирателей), то явка на этом участке станет равной 66%. Соответственно, этот участок перейдёт в другой разряд гистограммы, а количество бюллетеней в разряде 47% уменьшится на количество голосов, которое было на этом участке до вброса.
Если, предположим, число участков, на которых был вброс 19%, составляет половину от общего их числа (на остальных, скажем, вброса совсем не было), то результирующая кривая общего распределения вброса примет следующий вид:
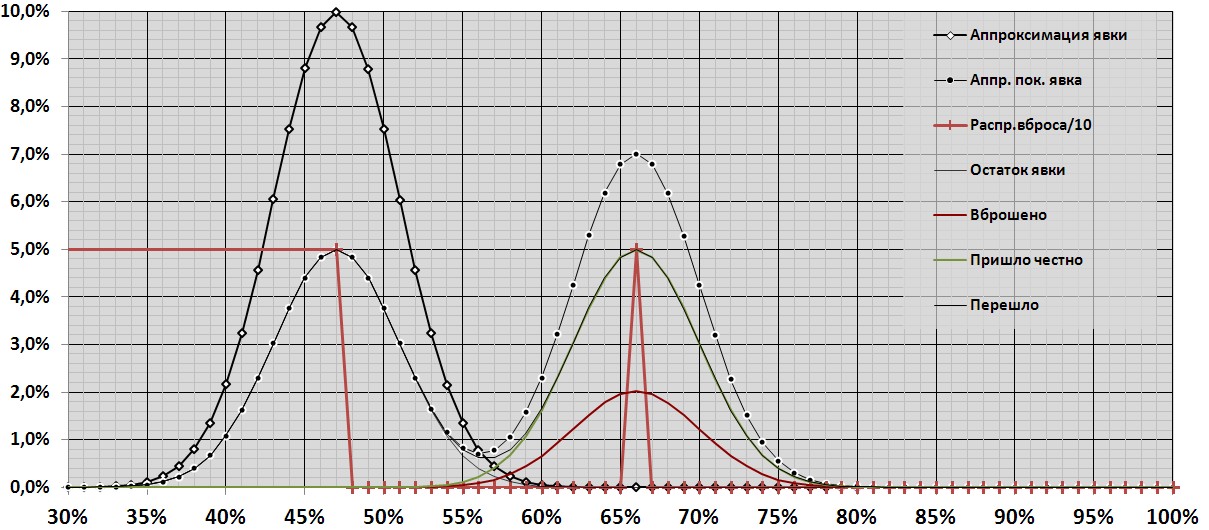
Результирующая кривая (с чёрными круглыми маркерами) приняла двугорбый вид. Распределение вброса для этого случая состоит из 2 значений: 50%- участки без вброса, 50% - участки со вбросом 19%, показаны светло-коричневой кривой с маркерами - крестиками, в удобном масштабе. Для наглядности, хотя распределение вброса идёт от 0%, оно показано от максимума исходной явки, 47%, тогда пик результирующего распределения совпадает с пиком распределения вброса, что удобно для анализа. Кроме этого, на диаграмме тонкими сплошными линиями показаны остаток исходного распределения, перешедшие и вброшенные голоса, а также сумма голосов за вычетом вброса.
Можно подобрать такое распределение вброса, которое минимизирует (например, по МНК) разницу между аппроксимированной кривой после вброса и реально зафиксированной на выборах. Диаграмма, соответствующая такому оптимально подобранному распределению взноса, такова:

Видно, что скачки вброса соответствуют как некоторым круглым значениям явки, таким как 50, 55, 65, 70, 75, 85%, так и некоторым некруглым. Остаточная сумма квадратов отклонения для этого случая (среднее 47%, СКО - 4%) равна 4,1E-4. Если взять другие предполагаемые значения среднего и СКО исходного распределения, то им будут соответствовать свои минимумы остаточного отклонения.
Можно изобразить это графически, сгруппировав минимумы по определённому СКО:

Здесь по вертикальной оси отложены минимальные остатки, по горизонтальной - значения процента вброса (0% вброса соответствует явка по Чурову, равная для Москвы 61,31%). Видно, что для каждого СКО существует свой минимум остатка, соответствующий определённому проценту вброса. В "области Шпилькина", при вбросе 14,3% наилучшее соответствие кривых, выражаемое минимумом остатка, равным 4,1...4,3Е-4, слабо зависит от предполагаемой дисперсии исходного распределения.
Соединим для наглядности минимумы для разных предполагаемых СКО. Видно, что возможный минимум резко уменьшается при малых СКО исходного распределения, начиная с 2,5% (что объясняется упрощением подгонки острым пиком исходного распределения явки). Также минимум резко растёт при СКО, больших 5%, что объясняется трудностями аппроксимации острых горбов растянутой гауссианой исходной явки. Минимальному значению остатка, равному 3,6E-4, соответствует вброс 9,31% при СКО исходной явки 5% (среднее значение исходной явки 52%). На диаграмме это выглядит так:
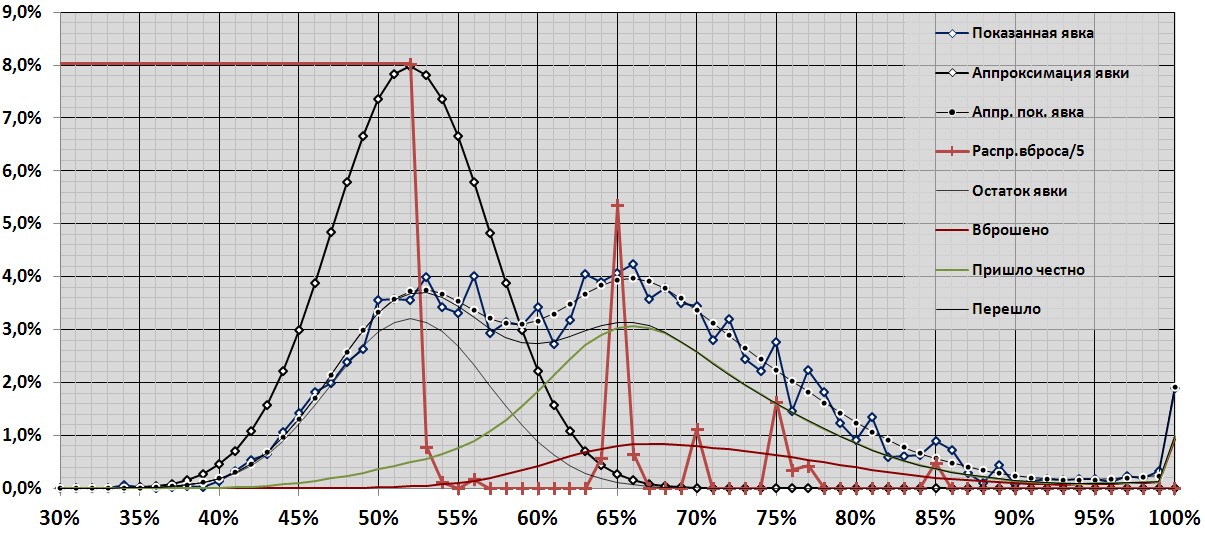
Характер распределения вброса при этих значениях заметно отличается от вброса при предположении исходных данных 47%/4%, хотя можно отметить и определённое сходство.
Таким образом, анализ возможных вариантов распределения вброса только на основании распределения явки не позволяет точно определить параметры исходного распределения, однако позволяет ограничить диапазон вброса значениями 9,3-15,3% с соответствующими СКО исходного распределения 5-2,5%, а также определить долю вброшенных бюллетеней в показанном проценте явки.
Уточним характеристики исходного распределения анализом распределений голосов за партии, исходя из предположения гомологичности действий избирателей.
Но это будет задачей отдельного поста.
Попробуем подробнее разобраться в этом вопросе. Сделаем это на примере голосования в Москве. Распределение голосов здесь имело интересную изломанную двугорбую форму:

Здесь горизонтальная ось является осью явки (от числа зарегистрированных на избирательном участке). По вертикальной оси отложен % голосов избирателей, суммированных по участкам, попавшим в +-0,5% интервал оси явки, т.е. это гистограмма глобальной явки, изображённая в виде графика (всего под кривой 100%).
По поводу возможных причин двугорбости (и того, что эта двугорбость начала проявляться уже в промежуточных отчётах УИК об явке) сломано много копий в посте популяризатора распределений явки oude_rus: Дива -- не прочесть тайну. Рассматривалось множество версий, приводились гипотезы о разной активности избирателей в разных округах Москвы, о разных типах избирателей (вроде мужчин и женщин), о волшебстве Чурова, о разных типах председателей УИК, но к однозначному мнению не пришли.
Посмотрим, как можно прийти к двугорбости, оперируя цифрами различия фальсификаций на разных участках.
Для начала зададимся возможными характеристиками исходного гауссового распределения явки. Оно характеризуется всего лишь двумя характеристиками - средним значением и СКО - среднеквадратическим отклонением.
Среднюю величину вброса 14,35% дает podmoskovnik в своей статье "Математика выборов - 2011" в газете "Троицкий вариант". СКО исходного распределения его методом вычислить нельзя, но из консультаций было уточнено, что оно может находиться в диапазоне 3,4-4,2%.
Примем среднее значение равным 47% (соответствует вбросу 14,3%) со СКО = 4% (по оси явки). Исходная и получившиеся кривые тогда будут такими (площадь под гауссовой кривой - 100%, под кривой показанной явки увеличена соответственно предполагаемому вбросу):

Каким образом из одной кривой получается другая и как влияет вброс на кривую распределения явки? Поскольку вброшенные бюллетени не существуют сами по себе, а складываются с уже имеющимися на участке, процент явки на этом участке увеличивается на процент вброшенных бюллетеней. Например, если исходный процент явки был 47%, а дополнительно вброшено (любым образом, скажем, добавлено при вводе данных в систему ГАС "Выборы") 19% бюллетеней (от зарегистрированного количества избирателей), то явка на этом участке станет равной 66%. Соответственно, этот участок перейдёт в другой разряд гистограммы, а количество бюллетеней в разряде 47% уменьшится на количество голосов, которое было на этом участке до вброса.
Если, предположим, число участков, на которых был вброс 19%, составляет половину от общего их числа (на остальных, скажем, вброса совсем не было), то результирующая кривая общего распределения вброса примет следующий вид:

Результирующая кривая (с чёрными круглыми маркерами) приняла двугорбый вид. Распределение вброса для этого случая состоит из 2 значений: 50%- участки без вброса, 50% - участки со вбросом 19%, показаны светло-коричневой кривой с маркерами - крестиками, в удобном масштабе. Для наглядности, хотя распределение вброса идёт от 0%, оно показано от максимума исходной явки, 47%, тогда пик результирующего распределения совпадает с пиком распределения вброса, что удобно для анализа. Кроме этого, на диаграмме тонкими сплошными линиями показаны остаток исходного распределения, перешедшие и вброшенные голоса, а также сумма голосов за вычетом вброса.
Можно подобрать такое распределение вброса, которое минимизирует (например, по МНК) разницу между аппроксимированной кривой после вброса и реально зафиксированной на выборах. Диаграмма, соответствующая такому оптимально подобранному распределению взноса, такова:

Видно, что скачки вброса соответствуют как некоторым круглым значениям явки, таким как 50, 55, 65, 70, 75, 85%, так и некоторым некруглым. Остаточная сумма квадратов отклонения для этого случая (среднее 47%, СКО - 4%) равна 4,1E-4. Если взять другие предполагаемые значения среднего и СКО исходного распределения, то им будут соответствовать свои минимумы остаточного отклонения.
Можно изобразить это графически, сгруппировав минимумы по определённому СКО:

Здесь по вертикальной оси отложены минимальные остатки, по горизонтальной - значения процента вброса (0% вброса соответствует явка по Чурову, равная для Москвы 61,31%). Видно, что для каждого СКО существует свой минимум остатка, соответствующий определённому проценту вброса. В "области Шпилькина", при вбросе 14,3% наилучшее соответствие кривых, выражаемое минимумом остатка, равным 4,1...4,3Е-4, слабо зависит от предполагаемой дисперсии исходного распределения.
Соединим для наглядности минимумы для разных предполагаемых СКО. Видно, что возможный минимум резко уменьшается при малых СКО исходного распределения, начиная с 2,5% (что объясняется упрощением подгонки острым пиком исходного распределения явки). Также минимум резко растёт при СКО, больших 5%, что объясняется трудностями аппроксимации острых горбов растянутой гауссианой исходной явки. Минимальному значению остатка, равному 3,6E-4, соответствует вброс 9,31% при СКО исходной явки 5% (среднее значение исходной явки 52%). На диаграмме это выглядит так:

Характер распределения вброса при этих значениях заметно отличается от вброса при предположении исходных данных 47%/4%, хотя можно отметить и определённое сходство.
Таким образом, анализ возможных вариантов распределения вброса только на основании распределения явки не позволяет точно определить параметры исходного распределения, однако позволяет ограничить диапазон вброса значениями 9,3-15,3% с соответствующими СКО исходного распределения 5-2,5%, а также определить долю вброшенных бюллетеней в показанном проценте явки.
Уточним характеристики исходного распределения анализом распределений голосов за партии, исходя из предположения гомологичности действий избирателей.
Но это будет задачей отдельного поста.