Гладко было на бумаге
В этой части я расскажу решение задачи об остывании шара в том виде, в котором оно виделось авторам.
Итак, у нас имеется краевая задача на единичном шаре:

Коэффициент температуропроводности
, а начальное условие задано своими замерами с некоторым шагом.
Благодаря симметрии, переходя в сферические координаты получим:
}{\partial&space;r^2}=\frac{1}{a}\frac{\partial&space;T}{\partial&space;t},&space;\\&space;T\left&space;(&space;r,0&space;\right&space;)=f(r),&space;\\&space;T(1,t)=0.&space;\end{matrix}\right.)
В принципе, здесь уже можно было бы задуматься о численном решении, но мы себе еще более упростим жизнь стандартной заменой.
Пусть теперь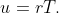
Тогда,аккуратно проделав все выкладки, имеем:
=rf(r),&space;\\&space;u(0,t)=0,&space;\\&space;u(1,t)=0.&space;\end{matrix}\right.)
Т.е. в итоге получаем банальнейшую однородную двухточечную краевую задачу для одномерного уравнения теплопроводности. Замена переменных, которой мы сейчас воспользовались, общеизвестна и описывается в любом уважающем себя учебнике (надо бы и в нашем акцент усилить, хех), но ежели, вдруг, она поражает новизной, я бы посоветовал разок проделать ее полностью.
Ну теперь-то всяко уже пора численно решать!
Взяв простейший явный четырехточечный шаблон

получим простейшую разностную схему:
,)
где
Понятно, что k - счетчик шагов времени, а i - радиуса. Если кого-то эта формула вдруг напугала, то напрасно, мы просто тупо заменили вторую производную по пространственной координате на центральную разность второго порядка,а по времени у нас вообще схема Эйлера.
Собственно, пункт А уже практически сдался. Здесь есть, теоретически, одна мелкая подляна, но шансов споткнуться об нее даже у самого незамутненного решателя достаточно мало. Дело в том, что согласно теории разностных схем, описанная выше конструкция устойчива только при условии
Так как шаг по радиусу нам задан принудительно в условии задачи (замеры начального условия сделаны с шагом 0,04 м), то наша схема устойчива при
Эпоха перфокарт и дефицита машинного времени граничит с античностью и представить себе человека, который возьмет сегодня в такой схеме шаг по времени больше сорока секунд мне физически тяжело.
Найдя численно
остается лишь перейти обратной заменой к T. Тут возникает некоторое неудобство. Если бы нас интересовала температура не в центре, мы бы поделили на r и дело с концом. Но делить на ноль, особенно численно, немного некомфортно. Было бы у нас аналитическое решение, то мы бы просто перешли к пределу, а так авторы задачи рекомендуют некий хитромудрый анализ (см. ниже). Для пункта А, тем не менее, на их мнение мы облокотимся, так как температура у нас функция хорошая-гладкая, и мы вполне можем ее проэкстраполировать Лагранжем по 3-4 соседним точкам [Spoiler (click to open)]трех хватит за глаза.
Короче говоря, чтоб вам не перенапрягаться с программированием, я тут сляпал на коленке версию на C++, можете поиграться:
#include
#include
const std::vector zero_condition = {
100.0,
99.737,
98.951,
97.648,
95.842,
93.549,
90.791,
87.594,
83.987,
80.004,
75.683,
71.062,
66.184,
61.093,
55.834,
50.455,
45.002,
39.523,
34.064,
28.671,
23.387,
18.256,
13.316,
8.604,
4.156,
0.0
};
constexpr double dr = 0.04;
constexpr double dt = 1.0;
constexpr double a = 2e-5;
constexpr double c = a * dt / (dr * dr);
constexpr double t_stop = 10000;
constexpr size_t Nt = static_cast(t_stop / dt + 0.5);
void iterate_layer(std::vector& layer, std::vector& new_layer)
{
for (size_t i = 1; i < layer.size() - 1; ++i)
{
new_layer[i] = layer[i] + c * (layer[i - 1] - 2 * layer[i] + layer[i + 1]);
}
}
int main()
{
std::vector layer[] = { zero_condition, zero_condition };
for (size_t i = 0; i < zero_condition.size(); ++i)
{
layer[0][i]= layer[1][i] *=i*dr;
}
double t = 0.0;
size_t fl = 0;
for (size_t i = 0; i < Nt; ++i)
{
iterate_layer(layer[i % 2], layer[(i + 1) % 2]);
t += dt;
fl = (i + 1) % 2;
}
for (size_t i = 1; i < zero_condition.size(); ++i)
{
layer[fl][i] /= i * dr;
}
auto Lagrange = [&](double x) {return (layer[fl][1] * (x - 2 * dr) * (x - 3 * dr) -
2.0 * layer[fl][2] * (x - dr) * (x - 3 * dr) + layer[fl][3] * (x - 2 * dr) * (x - dr)) / (2 * dr * dr); };
std::cout << Lagrange(0.0);
}
Собственно, пункт А закрыт полностью. Как видите, он вполне по силам обычному старшекурснику и на всеросе такой задачке однозначно не место. Если бы не пункт Б, к которому мы, помолясь, и переходим.
В нем нам предлагается решить ту же краевую задачу но с отрицательным временем, она же ретроспективная задача теплопроводности. Это классическая некорректная задача и попытки ее решить используя разностную схему обречены на провал по причине численной неустойчивости. Основной подход "по взрослому" к таким задачам, если на пальцах - это установление некоторых дополнительных условий на поведение решения (в данном конкретном случае прокатило бы требование монотонности по пространственной координате), после чего задача особым образом регуляризуется. Заинтересовавшихся я отсылаю к классической книжке "Методы решения некорректных задач" за авторством А. Н. Тихонова и В. Я. Арсенина. Загвоздка в том, что этот матаппарат безнадежно тяжел для олимпиадной задачки, а значит надо шаманить что-нибудь заметно проще. К природе некорректности ретроспективной задачи теплопроводности мы еще вернемся в следующей части, а пока добьем таки пункт Б.
Авторами задачи, видимо предполагалось, что вдоволь наигравшись с температурами a la "-10^400", олимпиец возьмется за голову и попробует проанализировать решение уравнения в области положительного времени, там где оно хорошо обусловлено.
На промежутке времени от 0 до 10000 с выглядит наше численное решение следующим образом:

В частности, видно, что в каждый момент времени функция температуры монотонно убывает от центра к границе (см. про монотонность выше). Вдоволь повертев график в разные стороны, наш герой должен был осознать (нет, я не ожидаю, что вы это из приведенного графика увидите), что скорость остывания по времени не зависит от радиуса и решение задачи с положительным временем имеет неожиданно простой вид:
=f\left&space;(&space;r&space;\right&space;)e^{-\tau&space;t}.)
Поднапрягшись, должно получиться более-менее такое значение:

В частности, для интересующего нас центра шара получается мегапростое выражение:
=100e^{-0,00019739208t}.)
С точки зрения авторов, лишь сейчас мы окончательно должны были решить пункт А. Ну нет уж, спасибо Лагранжу (хотя тем, кто дополз аж сюда это позволит слегка улучшить посчитанные в пункте А значения).
Остается последний шаг. Оснований считать, что поведение решения отличается в прошлом у нас нет (строго говоря, эти основания могут быть не видны при измерениях в нулевой момент времени, спрятавшись в погрешностях градусника, но это уже откровенная казуистика; впрочем, к этой теме мы в следующей части еще вернемся), поэтом температуру центра шара в прошлом мы считаем по уже полученной формуле и она таки даст нам правильные значения.
Решаемая таким способом, задачка вполне тянет на всерос, пункт Б откровенно непрост и одновременно интересен, позволяя поиграться с довольно нетривиальными вещами. Однако, есть один нюанс...
Продолжение следует!
Продолжение.
ЗЫ. Кто догадался, куда ветер дует, тот молодец, но просьба в комментариях воздержаться от спойлеров и не ломать интригу. Если есть желание проверить свою догадку - пишите в личку, я всем отвечу. Комментарии не закрываю.
Итак, у нас имеется краевая задача на единичном шаре:

Коэффициент температуропроводности

, а начальное условие задано своими замерами с некоторым шагом.
Благодаря симметрии, переходя в сферические координаты получим:
В принципе, здесь уже можно было бы задуматься о численном решении, но мы себе еще более упростим жизнь стандартной заменой.
Пусть теперь
Тогда,аккуратно проделав все выкладки, имеем:
Т.е. в итоге получаем банальнейшую однородную двухточечную краевую задачу для одномерного уравнения теплопроводности. Замена переменных, которой мы сейчас воспользовались, общеизвестна и описывается в любом уважающем себя учебнике (надо бы и в нашем акцент усилить, хех), но ежели, вдруг, она поражает новизной, я бы посоветовал разок проделать ее полностью.
Ну теперь-то всяко уже пора численно решать!
Взяв простейший явный четырехточечный шаблон

получим простейшую разностную схему:
где
Понятно, что k - счетчик шагов времени, а i - радиуса. Если кого-то эта формула вдруг напугала, то напрасно, мы просто тупо заменили вторую производную по пространственной координате на центральную разность второго порядка,а по времени у нас вообще схема Эйлера.
Собственно, пункт А уже практически сдался. Здесь есть, теоретически, одна мелкая подляна, но шансов споткнуться об нее даже у самого незамутненного решателя достаточно мало. Дело в том, что согласно теории разностных схем, описанная выше конструкция устойчива только при условии
Так как шаг по радиусу нам задан принудительно в условии задачи (замеры начального условия сделаны с шагом 0,04 м), то наша схема устойчива при
Эпоха перфокарт и дефицита машинного времени граничит с античностью и представить себе человека, который возьмет сегодня в такой схеме шаг по времени больше сорока секунд мне физически тяжело.
Найдя численно
остается лишь перейти обратной заменой к T. Тут возникает некоторое неудобство. Если бы нас интересовала температура не в центре, мы бы поделили на r и дело с концом. Но делить на ноль, особенно численно, немного некомфортно. Было бы у нас аналитическое решение, то мы бы просто перешли к пределу, а так авторы задачи рекомендуют некий хитромудрый анализ (см. ниже). Для пункта А, тем не менее, на их мнение мы облокотимся, так как температура у нас функция хорошая-гладкая, и мы вполне можем ее проэкстраполировать Лагранжем по 3-4 соседним точкам [Spoiler (click to open)]трех хватит за глаза.
Короче говоря, чтоб вам не перенапрягаться с программированием, я тут сляпал на коленке версию на C++, можете поиграться:
#include
#include
const std::vector
100.0,
99.737,
98.951,
97.648,
95.842,
93.549,
90.791,
87.594,
83.987,
80.004,
75.683,
71.062,
66.184,
61.093,
55.834,
50.455,
45.002,
39.523,
34.064,
28.671,
23.387,
18.256,
13.316,
8.604,
4.156,
0.0
};
constexpr double dr = 0.04;
constexpr double dt = 1.0;
constexpr double a = 2e-5;
constexpr double c = a * dt / (dr * dr);
constexpr double t_stop = 10000;
constexpr size_t Nt = static_cast
void iterate_layer(std::vector
{
for (size_t i = 1; i < layer.size() - 1; ++i)
{
new_layer[i] = layer[i] + c * (layer[i - 1] - 2 * layer[i] + layer[i + 1]);
}
}
int main()
{
std::vector
for (size_t i = 0; i < zero_condition.size(); ++i)
{
layer[0][i]= layer[1][i] *=i*dr;
}
double t = 0.0;
size_t fl = 0;
for (size_t i = 0; i < Nt; ++i)
{
iterate_layer(layer[i % 2], layer[(i + 1) % 2]);
t += dt;
fl = (i + 1) % 2;
}
for (size_t i = 1; i < zero_condition.size(); ++i)
{
layer[fl][i] /= i * dr;
}
auto Lagrange = [&](double x) {return (layer[fl][1] * (x - 2 * dr) * (x - 3 * dr) -
2.0 * layer[fl][2] * (x - dr) * (x - 3 * dr) + layer[fl][3] * (x - 2 * dr) * (x - dr)) / (2 * dr * dr); };
std::cout << Lagrange(0.0);
}
Собственно, пункт А закрыт полностью. Как видите, он вполне по силам обычному старшекурснику и на всеросе такой задачке однозначно не место. Если бы не пункт Б, к которому мы, помолясь, и переходим.
В нем нам предлагается решить ту же краевую задачу но с отрицательным временем, она же ретроспективная задача теплопроводности. Это классическая некорректная задача и попытки ее решить используя разностную схему обречены на провал по причине численной неустойчивости. Основной подход "по взрослому" к таким задачам, если на пальцах - это установление некоторых дополнительных условий на поведение решения (в данном конкретном случае прокатило бы требование монотонности по пространственной координате), после чего задача особым образом регуляризуется. Заинтересовавшихся я отсылаю к классической книжке "Методы решения некорректных задач" за авторством А. Н. Тихонова и В. Я. Арсенина. Загвоздка в том, что этот матаппарат безнадежно тяжел для олимпиадной задачки, а значит надо шаманить что-нибудь заметно проще. К природе некорректности ретроспективной задачи теплопроводности мы еще вернемся в следующей части, а пока добьем таки пункт Б.
Авторами задачи, видимо предполагалось, что вдоволь наигравшись с температурами a la "-10^400", олимпиец возьмется за голову и попробует проанализировать решение уравнения в области положительного времени, там где оно хорошо обусловлено.
На промежутке времени от 0 до 10000 с выглядит наше численное решение следующим образом:

В частности, видно, что в каждый момент времени функция температуры монотонно убывает от центра к границе (см. про монотонность выше). Вдоволь повертев график в разные стороны, наш герой должен был осознать (нет, я не ожидаю, что вы это из приведенного графика увидите), что скорость остывания по времени не зависит от радиуса и решение задачи с положительным временем имеет неожиданно простой вид:
Поднапрягшись, должно получиться более-менее такое значение:
В частности, для интересующего нас центра шара получается мегапростое выражение:
С точки зрения авторов, лишь сейчас мы окончательно должны были решить пункт А. Ну нет уж, спасибо Лагранжу (хотя тем, кто дополз аж сюда это позволит слегка улучшить посчитанные в пункте А значения).
Остается последний шаг. Оснований считать, что поведение решения отличается в прошлом у нас нет (строго говоря, эти основания могут быть не видны при измерениях в нулевой момент времени, спрятавшись в погрешностях градусника, но это уже откровенная казуистика; впрочем, к этой теме мы в следующей части еще вернемся), поэтом температуру центра шара в прошлом мы считаем по уже полученной формуле и она таки даст нам правильные значения.
Решаемая таким способом, задачка вполне тянет на всерос, пункт Б откровенно непрост и одновременно интересен, позволяя поиграться с довольно нетривиальными вещами. Однако, есть один нюанс...
Продолжение следует!
Продолжение.
ЗЫ. Кто догадался, куда ветер дует, тот молодец, но просьба в комментариях воздержаться от спойлеров и не ломать интригу. Если есть желание проверить свою догадку - пишите в личку, я всем отвечу. Комментарии не закрываю.