(no subject)
Немного странной математики
Я сейчас читаю книжку Cox'а под названием "primes of the form x^2+n y^2", пытаюсь разобрать какие-то основы теории полей классов. Невероятно красивая штука. Насколько я пока понял (а понял я пока немного), философия примерно такая - неразветвлённые расширения с абелевой группой галуа должны соответствовать конечным подгруппам якобиана. А так как у числовых якобиан сам конечный, есть некоторое универсальное неразветвлённое расширение, называемое полем классов Гильберта. И с ним можно играться, и это жутко интересно.
Так как я в теории чисел (да что уж там, вообще ни в чём) не разбираюсь, я постоянно пытался найти знакомые геометрические аналогии с Риманновыми поверхностями. В какой-то момент мне стало интересно - а может ли неразветвлённое накрытие над Риманновой поверхностью (компактной) быть индуцировано из разветвлённого накрытия над сферой. В самом простом случае, когда группа монодромии циклическая, Z/nZ, хотелось бы просто индуцировать из накрытия z->z^n. Топологически никаких препятствий этому конечно нет, а вот представить себе такое отображение тора на сферу, которое индуцирует неразветвлённое накрытие над тором из z->z^n аналитически мне никак не удавалось. Более того, моя интуиция до сих пор говорит мне, что его нет. И тем ни менее, я поигрался с функциями Вейерштрасса и получил следующую картинку:
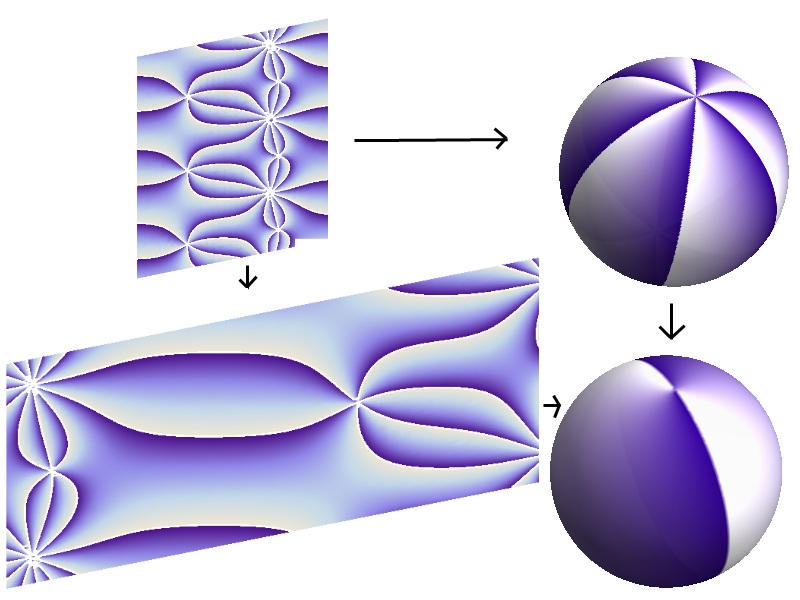
Как говорится, приведённая выше диаграмма коммутативна.
(о параллелограммах слева следует думать как о торе, а сферы просто изображают z->z^3; рассмотрение локальных монодромий показывает, что индуцированное накрытие - неразветвленное; точнее группу его монодромии порождает обход по "вертикальной" петле тора)
Подумываю о выставке абстрактного искусства :)
Я сейчас читаю книжку Cox'а под названием "primes of the form x^2+n y^2", пытаюсь разобрать какие-то основы теории полей классов. Невероятно красивая штука. Насколько я пока понял (а понял я пока немного), философия примерно такая - неразветвлённые расширения с абелевой группой галуа должны соответствовать конечным подгруппам якобиана. А так как у числовых якобиан сам конечный, есть некоторое универсальное неразветвлённое расширение, называемое полем классов Гильберта. И с ним можно играться, и это жутко интересно.
Так как я в теории чисел (да что уж там, вообще ни в чём) не разбираюсь, я постоянно пытался найти знакомые геометрические аналогии с Риманновыми поверхностями. В какой-то момент мне стало интересно - а может ли неразветвлённое накрытие над Риманновой поверхностью (компактной) быть индуцировано из разветвлённого накрытия над сферой. В самом простом случае, когда группа монодромии циклическая, Z/nZ, хотелось бы просто индуцировать из накрытия z->z^n. Топологически никаких препятствий этому конечно нет, а вот представить себе такое отображение тора на сферу, которое индуцирует неразветвлённое накрытие над тором из z->z^n аналитически мне никак не удавалось. Более того, моя интуиция до сих пор говорит мне, что его нет. И тем ни менее, я поигрался с функциями Вейерштрасса и получил следующую картинку:

Как говорится, приведённая выше диаграмма коммутативна.
(о параллелограммах слева следует думать как о торе, а сферы просто изображают z->z^3; рассмотрение локальных монодромий показывает, что индуцированное накрытие - неразветвленное; точнее группу его монодромии порождает обход по "вертикальной" петле тора)
Подумываю о выставке абстрактного искусства :)