Попугайная геометрия (15)

[super_kakadu]

Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠ AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.




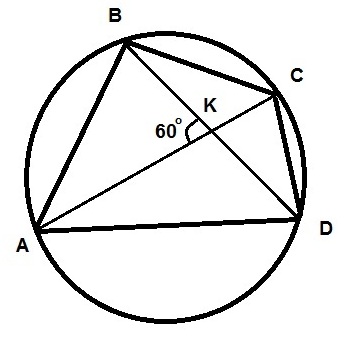
Решение.

1)


Треугольник АСD вписан в окружность радиуса R, тогда, используя расширенную теорему синусов, получаем, что

CD/sinCAD=2R

16/sinCAD=2R (**)

2) Аналогично всё и для треугольника АВD


АВ/sinАDВ=2R

25/sinADВ=2R

3) так как у нас одна и та же окружность, то

25/sinADВ=16/sinCAD , следовательно

25/16=sinADВ/sinСAD    (*)

4) Теперь рассмотрим треугольник АКD


Так как внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним, то

СAD=60°
60°-<СAD
Далее по ходу решения воспользуемся формулой

sin(α-β)=sinα×соsβ - sinβ×соsα   ,

но сначала вернёмся к выражению (*)

sinADВ/sinСAD=25/16

то есть

sin(60°-<СAD)/sinСAD=25/16

(sin60°×соsСAD - sinСAD×соs60°)/sinСAD=25/16
















5) Осталось найти sinСAD, для этого воспольщуемся методом треугольника.

Так как котангенс угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему, то мы можем нарисовать




Тогда можно найти и третью сторону треугольника



получаем, что синус угла равен



Подставив значение синуса угла САD в формулу (**) получаем