The relativity of simultaneity
<< Previous Article: "Spacetime and Coordinates"
We've disussed how an observer, Alice, can apply coordinates to a special-relativistic spacetime using just a clock and rays of light. Now we need to consider how things look to Bob if he's moving with respect to Alice at uniform speed. First let's consider two events, P and Q, that are simultaneous in Alice's frame as shown in figure 1.
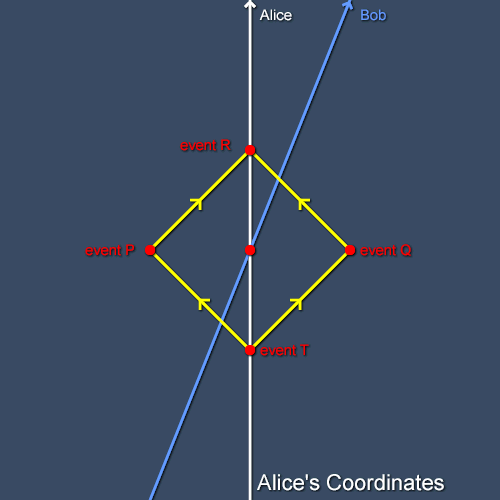
Figure 1 In Alice's frame the events P and Q are simultaneous.
Because of the principle of relativity one inertial frame is as good as another, Bob can use the same procedure as Alice to assign coordinates to the events P and Q. Let's watch him from Alice's frame as he does this. To draw the diagram of this situation we'll have to make use of the second postulate of special relativity: inertial observers always measure the same speed of light in a vacuum. This means that any light rays transmitted or received by Bob travel at 45 degrees to Alice's coordinate axes in just the same way that any rays that Alice transmits or receives herself do. (In this sense, special relativity is simpler than non-relativistic physics, in which we'd have to concern ourselves with the possibility that light emitted by moving observers might travel more rapidly than light emitted by stationary observers.)
As shown in figure 2, Bob must transmit light at event T1 to bounce it off event Q and receive it back at event R1. To bounce light off event P he must transmit it at event T2 and he receives the reflection at event R2. By symmetry - a powerful tool in physics - the same interval elapses on Bob's clock from T1 to R1 as from T2 to R2. Remember from our discussion of the method for assigning coordinates that event Q happens at the time in Bob's frame which is the average of his times at T1 and R1 and similarly event P happens in his frame at the time which is the average of his times at T2 and R2. As the two intervals are the same and T1 is earlier than T2, it follows that event Q happens earlier than event P. This is a striking conclusion: events that are simultaneous in one inertial frame are not simultaneous in other frames. As the description in any inertial frame is as good as that in any other it follows that there is no absolute notion of simultaneity. This is the famous phenomenon of the relativity of simultaneity. It follows directly from the principle of relativity and the constancy of the speed of light.
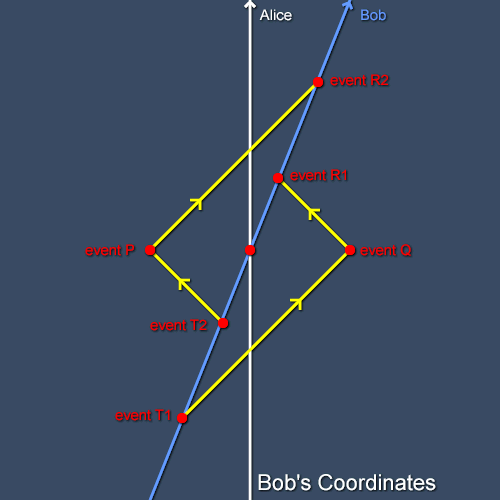
Figure 2 In Bob's frame Q occurs earlier than P.
To investigate the relativity of simultaneity in more detail we must next consider the sets of events which are simultaneous in Bob's frame. Once again we'll watch Bob from Alice's frame. Consider the collection of events and light rays shown in figure 3. The intervals from T1 to T2, T2 to C, C to R2 and R2 to R1 are all equal. This means that the average of the time from T1 to R1 is the time at event C, as is the average time from T2 to R2. Thus, by the procedure for assigning coordinates to events, the events A, B, C, D and E are all simultaneous in Bob's frame (although manifestly not in Alice's frame in which they increase in time from A to E).
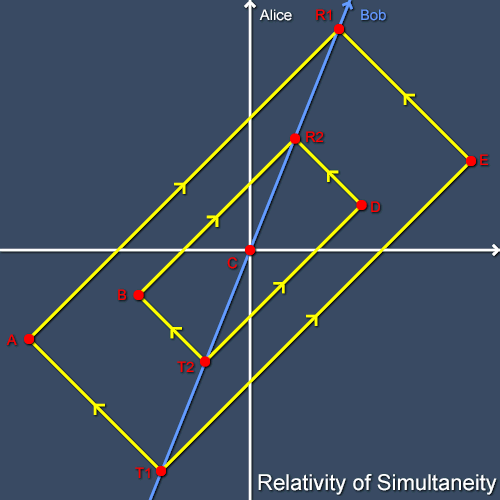
Figure 3 Simultaneous events in Bob's frame as seen from Alice's frame.
Alice and Bob slice up the same spacetime into space and time in different ways because of their relative motion, and neither slicing is in any sense better than the other. (There's nothing special about Alice's frame; we could just as well work entirely in Bob's frame and we'd reach the same conclusion.) This mixing of space and time is very different to the situation in pre-relativistic physics (or most people's intuitive picture of the world) in which everyone agrees on what is space and what is time. Moreover, the experimental evidence strongly suggests that it's a fundamental aspect of the way the world works. This won't be the last time that our naive intuitions turn out to be a poor guide to the nature of the universe.
Finally, let's draw Bob's coordinate grid as seen from Alice's frame. Bob's time axis is his worldline and his space axis passes through all the events simultaneous with event C in his frame, as shown in figure 4. The other spatial gridlines of his coordinate system are all parallel with this simultaneity surface and the temporal gridlines are parallel with his worldline. Therefore, his coordinate grid is skewed as seen by Alice. (Likewise, Alice's coordinate grid is skewed as seen by Bob.) This skewing, however, preserves the speed of light: light rays move one unit of space in one unit of time in Bob's coordinates just as they do in Alice's coordinates. It's just that what constitutes a unit of space or time is different. The relationship between the two sets of coordinates is called a Lorentz transformation. We will have much more to say about these transformations later.
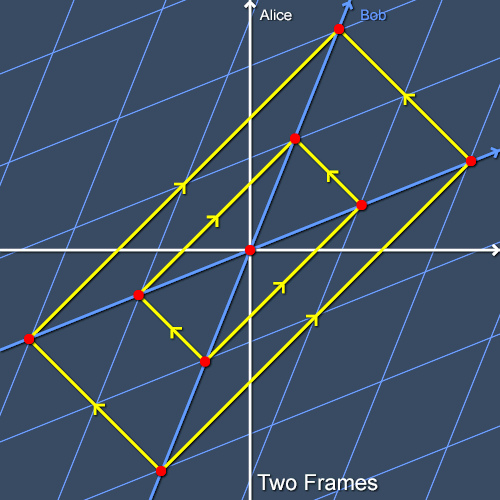
Figure 4 Bob's coordinate system as seen from Alice's frame.
From the discussion so far you will no doubt have the impression that very many things have values that are only valid relative to one inertial observer or another. On pondering the relativity of simultaneity you may start to worry that the theory of special relativity has fatally undermined even such everyday notions as "past" and "future". However, soon we'll see that the spacetime of special relativity has its own absolute causal structure in which past and future acquire new meanings. Later we will meet various absolute quantities that have values that are independent of the state of motion of the observer. A certain solidity will thus be restored to what might now seem a disturbingly insubstantial spacetime.
Next Article: "Relativity, FTL and Causality" >>