Занятие 104: Связывание детей, новый чёт-нечет, медленные колпачки и создание своих головоломок
Оригинал взят у tromentano в Занятие 104: Связывание детей, новый чёт-нечет, медленные колпачки и создание своих головоломок
Многие думают что я вот такой мягкий и терпеливый с детишками. Ан нет, на этой неделе дети даже связывались! :)

Можно ли разъединиться, не разрывая верёвочки, и не снимая их с запястьев? Ох, как они только не вертелись - но не получилось! Пришлось дать пару подсказок, чтобы научились делать этот фокус.

Это не так просто, но очень даже можно догадаться и самому!
[тут подсказка]
После этого мы стали играть в "чёт-нечет": я называю число и кидаю мяч кому-нибудь, если чёт - надо ловить, если нечёт - отбивать (как в "съедобное-несъедобное"). Естественно, всё было бы слишком просто, если бы я не стал называть вместо готовеньких чисел (даже самых огромных) математические выражения, вроде 7*3 или 5*8.
Настя робко сказала, что умножение они с мамой ещё не проходили, я пояснил, что умножать вовсе не обязательно: вот, напрмер, семь восьмёрок получится поделить пополам? Понятно же, что каждую восьмёрку, сколько бы их не было, можно поделить поплам по отдельности - значит и результат чётный. После этого Настя успокоилась и вполне себе бойко стала играть )
Естественно, когда с определением чётности-нечётности результатов простых умножений дети разобрались, я стал "закидывать удочку", загадывая что-нибудь вроде 100000*113, и 95*31.

Потом загадывать выражения стали и сами дети.

Следующее наше дело - игра "Медленные колпачки", для которой нужен реквизит от "Скоростных колпачков". Суть нашего варианта такая: перед каждым игроком выкладываетсяя четыре карты (или только вертикальные, или только горизонтальные). Игрок выбирает одну карту (не показывая другим), и собирает колпачки в комбинацию (тоже не показывая - под столом или пряча под коробкой). Задача остальных игроков - определить, какую карту он загадал.

Каждый игрок в свой ход может задать один вопрос любому другому игроку, вопросы могут быть типа "жёлтый выше чёрного?" или "красный правее синего?". Тот, кому вопрос задали, отвечает только "да" или "нет". Следующий игрок может задать свой один вопрос этому же игроку, или кому-то другому. Если игрок после своего вопроса уверен, какая карта загадана - он может указать на неё, если он правильно показал - то получает эту карту в качестве "добычи" для подсчёта в конце игры (на стол выкладывается новая карта, тот, у кого карту забрали, перевыбирает новую карту и снова собирает комбинацию). А если неправильно - то теряет все уже набранные карты (поэтому указывать имеет смысл только если действительно уверен, а не наугад).
Таким образом, нужно и правильно вопросы задавать, и ответы запоминать, да ещё и думать, кому сейчас вопрос задать, чтобы самому забрать карту, а не просто помочь сведениями следующему игроку.

Игра отлично пошла, даже со всеми условиями правил получилось с первого раза правильно сбалансировать (количество карт, регламент задавания вопросов и пр.)

А тут как раз шикарная игровая "Дома Гнома" опустела - переместились в неё на разминку, самые обычные, нематематические "из круга вышибалы", потому что сегодня у нас ещё одно серьёзное дело запланировано.

На одном из прошлых занятий дети решали " головоломки короля Квадратуса". В этот раз они сами их создавали:

Сделать это можно было по-разному. Проще всего карандашом начертить ковры, потом в них расставить числа, потом сами ковры стереть. Но можно и мысленно "раскладывать" ковры, расставля числа.

Ребята стали придумывать всякие коварные варианты головоломки - с непрямоугольным общим контуром, или с большими числами:
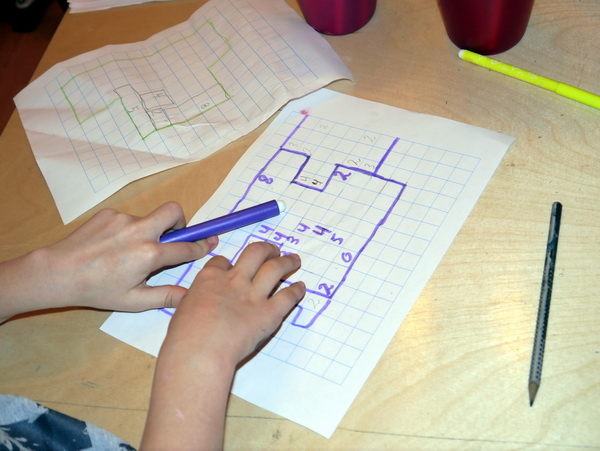
В общем, некоторым родителям пришлось решать созданные на занятии и после занятия головоломки )

Многие думают что я вот такой мягкий и терпеливый с детишками. Ан нет, на этой неделе дети даже связывались! :)
Можно ли разъединиться, не разрывая верёвочки, и не снимая их с запястьев? Ох, как они только не вертелись - но не получилось! Пришлось дать пару подсказок, чтобы научились делать этот фокус.
Это не так просто, но очень даже можно догадаться и самому!
[тут подсказка]

После этого мы стали играть в "чёт-нечет": я называю число и кидаю мяч кому-нибудь, если чёт - надо ловить, если нечёт - отбивать (как в "съедобное-несъедобное"). Естественно, всё было бы слишком просто, если бы я не стал называть вместо готовеньких чисел (даже самых огромных) математические выражения, вроде 7*3 или 5*8.
Настя робко сказала, что умножение они с мамой ещё не проходили, я пояснил, что умножать вовсе не обязательно: вот, напрмер, семь восьмёрок получится поделить пополам? Понятно же, что каждую восьмёрку, сколько бы их не было, можно поделить поплам по отдельности - значит и результат чётный. После этого Настя успокоилась и вполне себе бойко стала играть )
Естественно, когда с определением чётности-нечётности результатов простых умножений дети разобрались, я стал "закидывать удочку", загадывая что-нибудь вроде 100000*113, и 95*31.
Потом загадывать выражения стали и сами дети.
Следующее наше дело - игра "Медленные колпачки", для которой нужен реквизит от "Скоростных колпачков". Суть нашего варианта такая: перед каждым игроком выкладываетсяя четыре карты (или только вертикальные, или только горизонтальные). Игрок выбирает одну карту (не показывая другим), и собирает колпачки в комбинацию (тоже не показывая - под столом или пряча под коробкой). Задача остальных игроков - определить, какую карту он загадал.
Каждый игрок в свой ход может задать один вопрос любому другому игроку, вопросы могут быть типа "жёлтый выше чёрного?" или "красный правее синего?". Тот, кому вопрос задали, отвечает только "да" или "нет". Следующий игрок может задать свой один вопрос этому же игроку, или кому-то другому. Если игрок после своего вопроса уверен, какая карта загадана - он может указать на неё, если он правильно показал - то получает эту карту в качестве "добычи" для подсчёта в конце игры (на стол выкладывается новая карта, тот, у кого карту забрали, перевыбирает новую карту и снова собирает комбинацию). А если неправильно - то теряет все уже набранные карты (поэтому указывать имеет смысл только если действительно уверен, а не наугад).
Таким образом, нужно и правильно вопросы задавать, и ответы запоминать, да ещё и думать, кому сейчас вопрос задать, чтобы самому забрать карту, а не просто помочь сведениями следующему игроку.
Игра отлично пошла, даже со всеми условиями правил получилось с первого раза правильно сбалансировать (количество карт, регламент задавания вопросов и пр.)
А тут как раз шикарная игровая "Дома Гнома" опустела - переместились в неё на разминку, самые обычные, нематематические "из круга вышибалы", потому что сегодня у нас ещё одно серьёзное дело запланировано.
На одном из прошлых занятий дети решали " головоломки короля Квадратуса". В этот раз они сами их создавали:
Сделать это можно было по-разному. Проще всего карандашом начертить ковры, потом в них расставить числа, потом сами ковры стереть. Но можно и мысленно "раскладывать" ковры, расставля числа.
Ребята стали придумывать всякие коварные варианты головоломки - с непрямоугольным общим контуром, или с большими числами:
В общем, некоторым родителям пришлось решать созданные на занятии и после занятия головоломки )