Компьютерная модель эволюции
Эволюция это очень просто: изменчивость, наследственность и естественный отбор. Вот и всё.
Хм, нет, в этой записи дальше ещё какие-то буквы, интересно, зачем.
В чём загадка с точки зрения программиста?
Длина человеческого генома - 1010 бит (примерно, с точностью до порядка). От некоторого первосущества, снабженного сопоставимым по своему устройству генетическим аппаратом, до нас с вами прошло порядка 1010 поколений (это еще более примерная оценка). В каждом поколении на Земле обитало вполне конечное, ограниченное сверху число особей. Также давно известно, что генетический код можно рассматривать как Тьюринг-полный язык программирования.
Итого на Земле исполнялся некоторый генетический алгоритм (в том смысле, в котором это выражение понимается в computer science), единицами отбора в котором были программы на некотором экзотическом Тьюринг-полном языке в некоторой экзотической среде исполнения. Начиная с нуля, этот алгоритм за O(N) поколений ограниченного размера выдал на выходе набор программ длины N=1010, обладающих интеллектом (если точнее, интеллектом обладают результаты их экспрессии, но для Тьюринг-полных языков это достаточно эфемерная разница). Тем, кто на практике занимался генетическими алгоритмами или даже computer science вообще, я думаю, не нужно объяснять, почему этот факт выглядит загадочно. Мы так точно не умеем.
Схожее недоумение возникает и на более школьном уровне. Каким бы набором генов ни был снабжен конкретный человек, он остается человеком - с двумя руками, двумя ногами и головой. Эта особь почти всегда может научиться ходить, говорить, думать - то есть на макроуровне основные признаки вида всегда присутствуют. И опять же на макроуровне он наследует признаки родителей. Как, черт побери, так получается? Так мы тоже не умеем: механическая (например, посимвольная или построчная) смесь двух программ не только не будет проявлять смешанное поведение, но вообще почти никогда не будет корректным кодом.
Существующие "генетические алгоритмы" даже близко не показывают ни такую эффективность, ни такую устойчивость "фенотипа" при сохранении выразительной мощности. Вот почему на протяжении нескольких лет у меня была надежда: а вдруг мы поймем, как в этом смысле работает эволюция, научимся строить аналогичные процессы in silico, и сможем таким способом получать какие-то реально интересные результаты? Думаю, что не только у меня -- в близких мне сообществах, состоящих совсем не из биологов, популярны разговоры об эволюции, книги Докинза (а у тех, кто увлекся серьезней, Кунина) и т.п.
С годами я "всё понял" и могу попробовать передать это понимание тем, кто интересуется тем же самым. Естественно, оно касается только узкого вопроса "как могут выглядеть компьютерные модели эволюции, проявляющие схожие свойства", а не широкого "как на самом деле работает жизнь". Конечно же, второй вопрос на много порядков сложнее; было бы абсурдно пытаться что-то сказать по этому поводу, не будучи биологом. Но и первый в чем-то интересен.
Эта запись -- черновик, коротко описывающий основные идеи; если она вызовет интерес, я постараюсь оформить их более строго, снабдить кодом референсной реализации и перевести на английский.
1. Клетка - непрерывный аналог конечного автомата
С интересующей нас точки зрения клетку можно представить себе как отделенный от внешнего мира мембраной "суп" веществ. Естественно, кроме цитоплазмы в клетке есть ещё много интересного, но наш конечный автомат (state machine) работает именно здесь. Как и у самого привычного программистам конечного автомата, у клетки есть набор состояний и набор правил переходов между этими состояниями. В отличие от простых конечных автоматов, клетка может одновременно находиться в нескольких состояниях в разной степени, а именно, "состоянию S" клетки соответствует концентрация некоторого вещества S внутри неё. "Правила перехода" реализуются за счет того, что различные вещества вступают в реакции друг с другом, а ферменты могут катализировать или ингибировать эти реакции. В зависимости от генетического кода клетки синтезируются разные ферменты, то есть исполняются различные конечные автоматы. В computer science подобные конструкции обычно называют "fuzzy finite state machines".
В реальной живой клетке вещества кроме сигнально-управляющих ролей могут играть и содержательные, например, роль строительного материала или источника энергии. Ближайшим аналогом веществ, играющих одну из содержательных ролей, для симулируемых конечных автоматов являются их выходы. Аналогом "входов" для живой клетки является концентрация тех или иных веществ во внешней среде.
Сложность и разнообразие ферментов таковы, что в некотором приближении процессы изменения этого конечного автомата можно считать непрерывными. Иными словами, для любой конструкции "конечного автомата" возможны малые изменения во множестве разных направлений; случайные "мутации" способны менять его поведение плавно.
Итого, хороший аналог одной клетки - fuzzy finite state machine (нечёткий конечный автомат).
2. Однотипные клетки, собранные в "ткани", являются аналогом рекурсивных алгоритмов
Конечные автоматы, как известно, ограничены в своих возможностях (примерно как регулярные выражения). Для большей выразительности их нужно как-то комбинировать.
В качестве примера рассмотрим следующую задачу: допустим, мы зачем-то хотим, чтобы наши эволюционирующие организмы выучили умение складывать числа в двоичной записи. Для этого подойдет такой организм-гусеница:

"Гусеница" состоит из одинаковых клеток, то есть из нечетких конечных автоматов с одинаковым кодом. У каждой клетки есть три входа и два выхода. Два входа соответствуют битам двух складываемых чисел, один из выходов мы будем интерпретировать как результат, второй нужен для того, чтобы клетка могла как-то "общаться" с соседней (например, в этой конкретной задаче - передать ей бит переноса).
Пока что примем как данность тот факт, что геометрия "гусеницы" такая, какая есть, так уж получилось, что она удачно приспособлена именно для данной конкретной задачи. Если среда настроена так, что таргет (то есть приспособленность "организма") зависит от того, насколько сильно результат его работы будет похож на сумму двух числе, то практически любой "генетический алгоритм" очень быстро выдаст нам популяцию "гусениц", отлично складывающих многозначные числа: конечный автомат, складывающий два бита, то есть пишущий их xor в "выход" и and в "бит переноса", очень прост. На рисунке выше "гусеница" складывает числа 10011 и 10110 и получает 101001.
Если вы вспомните, как именно на собеседованиях пишете код, который обходит деревья, или что-то делает со списками, или занимается тому подобными вещами, вы осознаете, что на его основе всегда можно механическим образом построить эквивалентный код, выглядящий как один и тот же конечный автомат, выполняющийся одновременно во всех узлах (или вершинах) соответствующей структуры данных.
Итак, хороший аналог тканей многоклеточных организмов, состоящих из однотипных клеток -- структуры данных и рекурсивные алгоритмы на них. Эволюция алгоритма, запускаемого над фиксированной структурой данных, не загадочней, чем эволюция нечеткого конечного автомата, и сводится к ней.
3. Онтогенез и "план тела" многоклеточных соответствуют высокоуровневой "архитектуре" программы
В предыдущем пункте мы приняли как данность, что "план тела" гусеницы оказался именно таким, очень удобным для решения интересовавшей нас задачи (сложения чисел). Чтобы это допущение не было неправдоподобным, нужно придумать некий способ перебирать "планы тела" в ходе эволюции, то есть каким-то образом выражать их в виде конечного числа простых правил, обеспечивающих непрерывную изменчивость при малых изменениях этих правил. Априори это звучит как тяжелая, если не невозможная, задача: в самом деле, как непрерывными изменениями превратить, скажем, список в бинарное дерево?
Ответ на этот вопрос показал Макс Гумин своими удивительно красивыми демками под названием MarkovJunior. Общая идея систем, которые он придумал, такая: возьмем регулярную решетку (например, квадратную сетку на двумерной плоскости). Будем считать, что каждый узел решетки может быть раскрашен в один из нескольких цветов, и что на каждом шаге мы случайным образом применяем одно из подходящих локальных "правил перезаписи" (rewrite rules). Каждое из rewrite rules заменяет соседние клетки, соответствующие определенному паттерну, на клетки другого цвета. Этот процесс аналогичен развитию организма из клетки-зародыша: в каждый момент времени каждая клетка "знает" только свою небольшую окрестность и только из этих данных "делает вывод", делиться ей или нет, и если да, то в какие специализированные клетки её потомкам дифференцироваться.
Удивительно простые наборы правил позволяют создавать удивительно сложные системы. Локальные особенности структуры порождают нетривиальную глобальную топологию. Например, 2d-лабиринты создаются "клетками" трёх цветов и такими двумя правилами:
RBB=GGR
RGG=WWR
Результат выглядит примерно так:
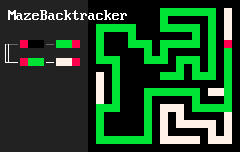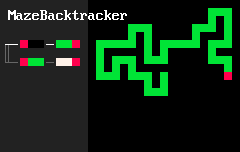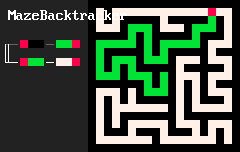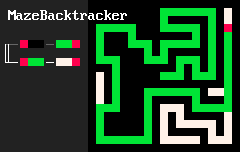
"Организмы", создаваемые подобными правилами на двумерной сетке, скорее всего, ограничены из-за того, что существуют непланарные графы, то есть не любую систему взаимосвязей между разными частями "организма" удастся выразить в таком виде. Но трехмерные сетки лишены этого недостатка. Вот несколько примеров "программ" на MarkovJunior, применённых на трехмерной сетке:

"Организмы", порожденные одной и той же программой, отличаются друг от друга, но, очевидно, принадлежат к одному "виду". У Гумина приоритет применения правил задан жестко, применяется правило с max(priority), но никто не мешает добавить непрерывности и применять правила с вероятностями, заданными как softmax(priority). Итого мы получаем формализм, позволяющий непрерывно переходить от одного распределения "планов тела" в популяции к другому; например, становится понятен план строения, промежуточный между списком и бинарным деревом -- это бинарное дерево, в котором почти у всех (но не у всех) вершин ровно один потомок.
Итак, хороший аналог многоклеточных организмов -- структуры, порождаемые несколькими правилами перезаписи на регулярной сетке (лучше трехмерной). Далее клетка каждого цвета снабжается непрерывным конечным автоматом, соответствующим цвету данной клетки, что позволяет итоговому организму "исполнять программы", используя свои ткани как структуры данных. В реальных многоклеточных организмах онтогенез и метаболизм не разделены абсолютно четко, одни и те же вещества и механизмы могут участвовать и там, и там, но в моделях такое разделение представляется естественным упрощением.
В итоге мы получаем Тьюринг-полный (for all intents and purposes) формализм, допускающий непрерывное изменение поведения при небольших изменениях "исходного кода", а значит, способный к эволюции по очень простой схеме: изменчивость, наследственность и естественный отбор. Вот и всё.
Хм, нет, в этой записи дальше ещё какие-то буквы, интересно, зачем.
В чём загадка с точки зрения программиста?
Длина человеческого генома - 1010 бит (примерно, с точностью до порядка). От некоторого первосущества, снабженного сопоставимым по своему устройству генетическим аппаратом, до нас с вами прошло порядка 1010 поколений (это еще более примерная оценка). В каждом поколении на Земле обитало вполне конечное, ограниченное сверху число особей. Также давно известно, что генетический код можно рассматривать как Тьюринг-полный язык программирования.
Итого на Земле исполнялся некоторый генетический алгоритм (в том смысле, в котором это выражение понимается в computer science), единицами отбора в котором были программы на некотором экзотическом Тьюринг-полном языке в некоторой экзотической среде исполнения. Начиная с нуля, этот алгоритм за O(N) поколений ограниченного размера выдал на выходе набор программ длины N=1010, обладающих интеллектом (если точнее, интеллектом обладают результаты их экспрессии, но для Тьюринг-полных языков это достаточно эфемерная разница). Тем, кто на практике занимался генетическими алгоритмами или даже computer science вообще, я думаю, не нужно объяснять, почему этот факт выглядит загадочно. Мы так точно не умеем.
Схожее недоумение возникает и на более школьном уровне. Каким бы набором генов ни был снабжен конкретный человек, он остается человеком - с двумя руками, двумя ногами и головой. Эта особь почти всегда может научиться ходить, говорить, думать - то есть на макроуровне основные признаки вида всегда присутствуют. И опять же на макроуровне он наследует признаки родителей. Как, черт побери, так получается? Так мы тоже не умеем: механическая (например, посимвольная или построчная) смесь двух программ не только не будет проявлять смешанное поведение, но вообще почти никогда не будет корректным кодом.
Существующие "генетические алгоритмы" даже близко не показывают ни такую эффективность, ни такую устойчивость "фенотипа" при сохранении выразительной мощности. Вот почему на протяжении нескольких лет у меня была надежда: а вдруг мы поймем, как в этом смысле работает эволюция, научимся строить аналогичные процессы in silico, и сможем таким способом получать какие-то реально интересные результаты? Думаю, что не только у меня -- в близких мне сообществах, состоящих совсем не из биологов, популярны разговоры об эволюции, книги Докинза (а у тех, кто увлекся серьезней, Кунина) и т.п.
С годами я "всё понял" и могу попробовать передать это понимание тем, кто интересуется тем же самым. Естественно, оно касается только узкого вопроса "как могут выглядеть компьютерные модели эволюции, проявляющие схожие свойства", а не широкого "как на самом деле работает жизнь". Конечно же, второй вопрос на много порядков сложнее; было бы абсурдно пытаться что-то сказать по этому поводу, не будучи биологом. Но и первый в чем-то интересен.
Эта запись -- черновик, коротко описывающий основные идеи; если она вызовет интерес, я постараюсь оформить их более строго, снабдить кодом референсной реализации и перевести на английский.
1. Клетка - непрерывный аналог конечного автомата
С интересующей нас точки зрения клетку можно представить себе как отделенный от внешнего мира мембраной "суп" веществ. Естественно, кроме цитоплазмы в клетке есть ещё много интересного, но наш конечный автомат (state machine) работает именно здесь. Как и у самого привычного программистам конечного автомата, у клетки есть набор состояний и набор правил переходов между этими состояниями. В отличие от простых конечных автоматов, клетка может одновременно находиться в нескольких состояниях в разной степени, а именно, "состоянию S" клетки соответствует концентрация некоторого вещества S внутри неё. "Правила перехода" реализуются за счет того, что различные вещества вступают в реакции друг с другом, а ферменты могут катализировать или ингибировать эти реакции. В зависимости от генетического кода клетки синтезируются разные ферменты, то есть исполняются различные конечные автоматы. В computer science подобные конструкции обычно называют "fuzzy finite state machines".
В реальной живой клетке вещества кроме сигнально-управляющих ролей могут играть и содержательные, например, роль строительного материала или источника энергии. Ближайшим аналогом веществ, играющих одну из содержательных ролей, для симулируемых конечных автоматов являются их выходы. Аналогом "входов" для живой клетки является концентрация тех или иных веществ во внешней среде.
Сложность и разнообразие ферментов таковы, что в некотором приближении процессы изменения этого конечного автомата можно считать непрерывными. Иными словами, для любой конструкции "конечного автомата" возможны малые изменения во множестве разных направлений; случайные "мутации" способны менять его поведение плавно.
Итого, хороший аналог одной клетки - fuzzy finite state machine (нечёткий конечный автомат).
2. Однотипные клетки, собранные в "ткани", являются аналогом рекурсивных алгоритмов
Конечные автоматы, как известно, ограничены в своих возможностях (примерно как регулярные выражения). Для большей выразительности их нужно как-то комбинировать.
В качестве примера рассмотрим следующую задачу: допустим, мы зачем-то хотим, чтобы наши эволюционирующие организмы выучили умение складывать числа в двоичной записи. Для этого подойдет такой организм-гусеница:

"Гусеница" состоит из одинаковых клеток, то есть из нечетких конечных автоматов с одинаковым кодом. У каждой клетки есть три входа и два выхода. Два входа соответствуют битам двух складываемых чисел, один из выходов мы будем интерпретировать как результат, второй нужен для того, чтобы клетка могла как-то "общаться" с соседней (например, в этой конкретной задаче - передать ей бит переноса).
Пока что примем как данность тот факт, что геометрия "гусеницы" такая, какая есть, так уж получилось, что она удачно приспособлена именно для данной конкретной задачи. Если среда настроена так, что таргет (то есть приспособленность "организма") зависит от того, насколько сильно результат его работы будет похож на сумму двух числе, то практически любой "генетический алгоритм" очень быстро выдаст нам популяцию "гусениц", отлично складывающих многозначные числа: конечный автомат, складывающий два бита, то есть пишущий их xor в "выход" и and в "бит переноса", очень прост. На рисунке выше "гусеница" складывает числа 10011 и 10110 и получает 101001.
Если вы вспомните, как именно на собеседованиях пишете код, который обходит деревья, или что-то делает со списками, или занимается тому подобными вещами, вы осознаете, что на его основе всегда можно механическим образом построить эквивалентный код, выглядящий как один и тот же конечный автомат, выполняющийся одновременно во всех узлах (или вершинах) соответствующей структуры данных.
Итак, хороший аналог тканей многоклеточных организмов, состоящих из однотипных клеток -- структуры данных и рекурсивные алгоритмы на них. Эволюция алгоритма, запускаемого над фиксированной структурой данных, не загадочней, чем эволюция нечеткого конечного автомата, и сводится к ней.
3. Онтогенез и "план тела" многоклеточных соответствуют высокоуровневой "архитектуре" программы
В предыдущем пункте мы приняли как данность, что "план тела" гусеницы оказался именно таким, очень удобным для решения интересовавшей нас задачи (сложения чисел). Чтобы это допущение не было неправдоподобным, нужно придумать некий способ перебирать "планы тела" в ходе эволюции, то есть каким-то образом выражать их в виде конечного числа простых правил, обеспечивающих непрерывную изменчивость при малых изменениях этих правил. Априори это звучит как тяжелая, если не невозможная, задача: в самом деле, как непрерывными изменениями превратить, скажем, список в бинарное дерево?
Ответ на этот вопрос показал Макс Гумин своими удивительно красивыми демками под названием MarkovJunior. Общая идея систем, которые он придумал, такая: возьмем регулярную решетку (например, квадратную сетку на двумерной плоскости). Будем считать, что каждый узел решетки может быть раскрашен в один из нескольких цветов, и что на каждом шаге мы случайным образом применяем одно из подходящих локальных "правил перезаписи" (rewrite rules). Каждое из rewrite rules заменяет соседние клетки, соответствующие определенному паттерну, на клетки другого цвета. Этот процесс аналогичен развитию организма из клетки-зародыша: в каждый момент времени каждая клетка "знает" только свою небольшую окрестность и только из этих данных "делает вывод", делиться ей или нет, и если да, то в какие специализированные клетки её потомкам дифференцироваться.
Удивительно простые наборы правил позволяют создавать удивительно сложные системы. Локальные особенности структуры порождают нетривиальную глобальную топологию. Например, 2d-лабиринты создаются "клетками" трёх цветов и такими двумя правилами:
RBB=GGR
RGG=WWR
Результат выглядит примерно так:
"Организмы", создаваемые подобными правилами на двумерной сетке, скорее всего, ограничены из-за того, что существуют непланарные графы, то есть не любую систему взаимосвязей между разными частями "организма" удастся выразить в таком виде. Но трехмерные сетки лишены этого недостатка. Вот несколько примеров "программ" на MarkovJunior, применённых на трехмерной сетке:

"Организмы", порожденные одной и той же программой, отличаются друг от друга, но, очевидно, принадлежат к одному "виду". У Гумина приоритет применения правил задан жестко, применяется правило с max(priority), но никто не мешает добавить непрерывности и применять правила с вероятностями, заданными как softmax(priority). Итого мы получаем формализм, позволяющий непрерывно переходить от одного распределения "планов тела" в популяции к другому; например, становится понятен план строения, промежуточный между списком и бинарным деревом -- это бинарное дерево, в котором почти у всех (но не у всех) вершин ровно один потомок.
Итак, хороший аналог многоклеточных организмов -- структуры, порождаемые несколькими правилами перезаписи на регулярной сетке (лучше трехмерной). Далее клетка каждого цвета снабжается непрерывным конечным автоматом, соответствующим цвету данной клетки, что позволяет итоговому организму "исполнять программы", используя свои ткани как структуры данных. В реальных многоклеточных организмах онтогенез и метаболизм не разделены абсолютно четко, одни и те же вещества и механизмы могут участвовать и там, и там, но в моделях такое разделение представляется естественным упрощением.
В итоге мы получаем Тьюринг-полный (for all intents and purposes) формализм, допускающий непрерывное изменение поведения при небольших изменениях "исходного кода", а значит, способный к эволюции по очень простой схеме: изменчивость, наследственность и естественный отбор. Вот и всё.