Лента Мебиуса и Гусеница Ники :)
Мы тут снова с детьми всякой интересной математикой занимаемся. Ставили эксперименты с лентой Мебиуса. Ника, кажется, прониклась гораздо больше, чем Лева! Она потом еще долго сидела сама всякое вырезала.
Итак, что такое лента Мебиуса?
Немецкий математик и астроном-теоретик Август Фердинанд Мёбиус (1790-1868) - ученик великого Гаусса, известный геометр, профессор Лейпцигского университета, директор обсерватории. Долгие годы преподавания, долгие годы работы - обычная жизнь профессора.
И вот надо же, это случилось под конец жизни! Пришла удивительная идея, это был самое значительное событие в его жизни! К сожалению, он так и не успел оценить значимость своего изобретения. Статья о знаменитой ленте Мебиуса была опубликована посмертно.
Как называют ленту Мебиуса (иначе лист Мебиуса или петлю Мебиуса) математики?
На языке математики это топологический объект, простейшая односторонняя поверхность с краем в обычном трёхмерном Евклидовом пространстве, где можно попасть из одной точки этой поверхности в любую другую, не пересекая края.
Достаточно сложное определение, не то что детям, даже взрослым оно с первого раза не очень понятно. Поэтому отбрасываем скучные определения и переходим к экспериментам!
Понадобится:
- несколько листов бумаги формата А4, разрезанных на полосы вдоль длинного края
- клей, фломастер и ножницы
Берем бумажную полоску, перекручиваем полоску в пол-оборота поперек (на 180 градусов) и склеиваем концы. - у нас получится лента Мебиуса.
На картинке показано как именно надо перекручивать:

А можно сделать две немного разные ленты Мебиуса: у одной перекручивать перед склейкой полоску по часовой стрелке, а у другой - против часовой стрелки. Так различаются правая и левая ленты Мебиуса.
Эксперимент 1.
Сначала проверим, что лента у нас действительно односторонняя.
Для этого я сделала кроме ленты еще и обычное бумажное кольцо(не перекрученное).

Сначала задаем детям вопрос: если мы будем вести линию по внешней стороне кольца, попадем ли мы на внутреннюю? Нет!!! бодро отвечают дети:)
Проводим эксперимент - действительно, не попадаем... Линия получается либо с внешней, либо с внутренней стороны.
А если мы возьмем ленту Мебиуса?
Тоже не попадем! - также бодро отвечают дети практически хором:)
Экспериментируем!
Ставим в каком-нибудь месте на ленте Мебиуса точку фломастером.

А теперь прочерчиваем вдоль всей нашей ленты линию, пока вам не встретится вновь ваша точка. Мы нигде не перешили через край ленты, и линия у нас с двух сторон! С внутренней и с внешней! Волшебство :)
Так не бывает... - задумчиво сказал Лева.
Это и называется односторонней поверхностью.

Если измерить эту линию точки до точки, она будет в два раза длиннее длины полоски, из которой клеилась Лента.
А если по этой черте заставить ползти, не сворачивая, муравья, то вы получите копию картины художника Мориса Эшера. Бедный муравей на бесконечной дороге! :)

Теперь берем ножницы, попробуем разрезать обычное кольцо по центральной линии. Кольцо превратилось в два отдельных кольца :)

Эксперимент 2.
А теперь попробуем разрезать ленту Мебиуса. Тоже будет два кольца? А вот и нет, лента развернется в длинную замкнутую ленту, закрученную вдвое больше, чем первоначальная. Почему лента Мебиуса при таком разрезе не распадается на отдельные части?
Разрез не касался края ленты, поэтому после разреза край (а значит и вся полоска бумаги) останется целым куском.

Эксперимент 3.
Полученную после первого опыта ленту Мебиуса (закрученную вдвое больше, чем первоначальная, т.е. на 360 градусов) вновь разрежем по ее центральной линии.
Теперь у нас получились две одинаковые, но сцепленные между собой ленты Мебиуса.

Эксперимент 4.
Сделаем новую ленту Мебиуса, но перед склейкой поверните ее не один раз, а три раза (не на 180 градусов, а на 540). Для того, чтобы было удобнее перекручивать, я склеила несколько полос в длину, чтобы лента Мебиуса получилась подлиннее. Теперь режем ее вдоль центральной линии.
Что получилось?
А получилась замкнутая лента, завитая в узел трилистника, т.е. в простой узел с тремя самопересечениями.

PS Если сделать ленту Мебиуса с еще большим числом полуоборотов перед склейкой, то удивительные фигуры, называемые парадромными кольцами.
5. Если разрезать ленту Мебиуса, не посередине, а отступая от края приблизительно на треть её ширины, то получатся две сцепленные ленты, одна - более короткая лента Мебиуса, и другая - длинная лента Мебиуса с двумя полуоборотами.


6. А теперь попробуем изготовить такую модель: в полосе АВСD прорезать щель и продеть сквозь неё один конец. Повернув, на пол оборота, склейте, как показано на рисунке.

Просовываем в щель ножницы и режем. Что получилось? Лента Мебиуса!

Есть еще один интересный объект, связанный с лентой Мебиуса. Это резистор Мебиуса.
Резистор Мебиуса, как объект изобретения, запатентован в США. Это электрический элемент - трехслойная полоса, в которой два проводящих слоя разделены слоем диэлектрика. Полоса скручена на 180 градусов и образует ленту Мебиуса. Такой резистор не имеет собственной индуктивности, и поэтому не создает магнитных помех, однако, обладает существенной паразитной емкостью.
Всем известный символ вторичной переработки - это видоизмененная лента Мебиуса!

Даже памятники ей есть.
например, в Москве (Архитектор А.Налич, на Комсомольском проспекте около кинотеатра “Горизонт”)

И в Минске (Скверик около Центральной Научной библиотеки имени Якуба Коласа)

Есть гипотеза, что спираль ДНК человека сама по себе тоже является фрагментом ленты Мебиуса

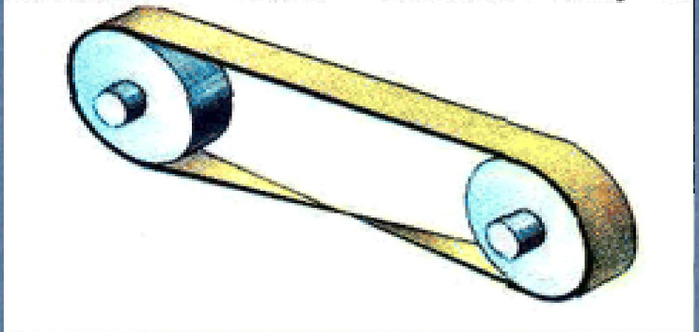
Существуют технические применения ленты Мёбиуса. Полоса ленточного конвейера выполняется в виде ленты Мёбиуса, что позволяет ему работать дольше, потому что вся поверхность ленты изнашивается равномерно. Также в системах записи на непрерывную плёнку применяются ленты Мёбиуса (чтобы удвоить время записи). Во многих матричных принтерах красящая лента также имеет вид листа Мёбиуса для увеличения её ресурса.
Ника еще долго потом резала всякие колечки, попросила меня сделать ей много-много.
Результатом ее игр явилась вот такая гусеница, сделанная ей совершенно самостоятельно.

А так она (гусеница) начиналась.

Итак, что такое лента Мебиуса?
Немецкий математик и астроном-теоретик Август Фердинанд Мёбиус (1790-1868) - ученик великого Гаусса, известный геометр, профессор Лейпцигского университета, директор обсерватории. Долгие годы преподавания, долгие годы работы - обычная жизнь профессора.
И вот надо же, это случилось под конец жизни! Пришла удивительная идея, это был самое значительное событие в его жизни! К сожалению, он так и не успел оценить значимость своего изобретения. Статья о знаменитой ленте Мебиуса была опубликована посмертно.
Как называют ленту Мебиуса (иначе лист Мебиуса или петлю Мебиуса) математики?
На языке математики это топологический объект, простейшая односторонняя поверхность с краем в обычном трёхмерном Евклидовом пространстве, где можно попасть из одной точки этой поверхности в любую другую, не пересекая края.
Достаточно сложное определение, не то что детям, даже взрослым оно с первого раза не очень понятно. Поэтому отбрасываем скучные определения и переходим к экспериментам!
Понадобится:
- несколько листов бумаги формата А4, разрезанных на полосы вдоль длинного края
- клей, фломастер и ножницы
Берем бумажную полоску, перекручиваем полоску в пол-оборота поперек (на 180 градусов) и склеиваем концы. - у нас получится лента Мебиуса.
На картинке показано как именно надо перекручивать:

А можно сделать две немного разные ленты Мебиуса: у одной перекручивать перед склейкой полоску по часовой стрелке, а у другой - против часовой стрелки. Так различаются правая и левая ленты Мебиуса.
Эксперимент 1.
Сначала проверим, что лента у нас действительно односторонняя.
Для этого я сделала кроме ленты еще и обычное бумажное кольцо(не перекрученное).

Сначала задаем детям вопрос: если мы будем вести линию по внешней стороне кольца, попадем ли мы на внутреннюю? Нет!!! бодро отвечают дети:)
Проводим эксперимент - действительно, не попадаем... Линия получается либо с внешней, либо с внутренней стороны.
А если мы возьмем ленту Мебиуса?
Тоже не попадем! - также бодро отвечают дети практически хором:)
Экспериментируем!
Ставим в каком-нибудь месте на ленте Мебиуса точку фломастером.

А теперь прочерчиваем вдоль всей нашей ленты линию, пока вам не встретится вновь ваша точка. Мы нигде не перешили через край ленты, и линия у нас с двух сторон! С внутренней и с внешней! Волшебство :)
Так не бывает... - задумчиво сказал Лева.
Это и называется односторонней поверхностью.

Если измерить эту линию точки до точки, она будет в два раза длиннее длины полоски, из которой клеилась Лента.
А если по этой черте заставить ползти, не сворачивая, муравья, то вы получите копию картины художника Мориса Эшера. Бедный муравей на бесконечной дороге! :)

Теперь берем ножницы, попробуем разрезать обычное кольцо по центральной линии. Кольцо превратилось в два отдельных кольца :)

Эксперимент 2.
А теперь попробуем разрезать ленту Мебиуса. Тоже будет два кольца? А вот и нет, лента развернется в длинную замкнутую ленту, закрученную вдвое больше, чем первоначальная. Почему лента Мебиуса при таком разрезе не распадается на отдельные части?
Разрез не касался края ленты, поэтому после разреза край (а значит и вся полоска бумаги) останется целым куском.

Эксперимент 3.
Полученную после первого опыта ленту Мебиуса (закрученную вдвое больше, чем первоначальная, т.е. на 360 градусов) вновь разрежем по ее центральной линии.
Теперь у нас получились две одинаковые, но сцепленные между собой ленты Мебиуса.

Эксперимент 4.
Сделаем новую ленту Мебиуса, но перед склейкой поверните ее не один раз, а три раза (не на 180 градусов, а на 540). Для того, чтобы было удобнее перекручивать, я склеила несколько полос в длину, чтобы лента Мебиуса получилась подлиннее. Теперь режем ее вдоль центральной линии.
Что получилось?
А получилась замкнутая лента, завитая в узел трилистника, т.е. в простой узел с тремя самопересечениями.

PS Если сделать ленту Мебиуса с еще большим числом полуоборотов перед склейкой, то удивительные фигуры, называемые парадромными кольцами.
5. Если разрезать ленту Мебиуса, не посередине, а отступая от края приблизительно на треть её ширины, то получатся две сцепленные ленты, одна - более короткая лента Мебиуса, и другая - длинная лента Мебиуса с двумя полуоборотами.


6. А теперь попробуем изготовить такую модель: в полосе АВСD прорезать щель и продеть сквозь неё один конец. Повернув, на пол оборота, склейте, как показано на рисунке.

Просовываем в щель ножницы и режем. Что получилось? Лента Мебиуса!

Есть еще один интересный объект, связанный с лентой Мебиуса. Это резистор Мебиуса.
Резистор Мебиуса, как объект изобретения, запатентован в США. Это электрический элемент - трехслойная полоса, в которой два проводящих слоя разделены слоем диэлектрика. Полоса скручена на 180 градусов и образует ленту Мебиуса. Такой резистор не имеет собственной индуктивности, и поэтому не создает магнитных помех, однако, обладает существенной паразитной емкостью.
Всем известный символ вторичной переработки - это видоизмененная лента Мебиуса!

Даже памятники ей есть.
например, в Москве (Архитектор А.Налич, на Комсомольском проспекте около кинотеатра “Горизонт”)

И в Минске (Скверик около Центральной Научной библиотеки имени Якуба Коласа)

Есть гипотеза, что спираль ДНК человека сама по себе тоже является фрагментом ленты Мебиуса

Существуют технические применения ленты Мёбиуса. Полоса ленточного конвейера выполняется в виде ленты Мёбиуса, что позволяет ему работать дольше, потому что вся поверхность ленты изнашивается равномерно. Также в системах записи на непрерывную плёнку применяются ленты Мёбиуса (чтобы удвоить время записи). Во многих матричных принтерах красящая лента также имеет вид листа Мёбиуса для увеличения её ресурса.

Ника еще долго потом резала всякие колечки, попросила меня сделать ей много-много.
Результатом ее игр явилась вот такая гусеница, сделанная ей совершенно самостоятельно.

А так она (гусеница) начиналась.
