Математическая лингвистика
Лингвистика математическая

Лингвистика математическая
Научная дисциплина, применяющая
математические методы Для исследования
языка и использующая электронные
вычислительные машины для моделирования
языка и тех операций, которые человек
осуществляет над языком.
Слова и числа
Пожалуй, до недавнего времени одной из самых "нематематических", самых описательных наук по праву считали лингвистику. А вот теперь говорят о лингвистике математической.
Подобно тому, как теория вероятностей произвела в физике переворот, так и введение в лингвистику вероятностных и количественных методов придало этой гуманитарной науке элементы строгости и точности.
Круг вопросов новой науки очень широк. Сначала познакомимся с одним интересным направлением - с количественным описанием языка.
По мнению специалистов, любой язык характеризуют некоторые простые количественные соотношения. Сколько слов в различных языках, каково различие между числом слов и числом морфем и фонем? Каково соотношение между словами и слогами, фонемами и морфемами?
[Spoiler (click to open)]
Вам не показались эти вопросы слишком "узкими", "вопросами ради вопросов"? Наверное, показались. Но математическое исследование языка - не забава для ученых, не досужее "буквоедство". Практическое значение такого подхода к языку очень велико. Именно количественные характеристики помогают определить природу, характер неизвестной письменности, помогают л ее дешифровке. Нужны они и для описания современных языков, для изучения их истории, для определения их родства.
Статистический подход к языку приводит иногда к поразительным результатам/Выяснилось, например, что у столь различных, с нашей точки зрения, языков, как русский, английский, самоанский, количество информации, приходящейся на букву "Н", оказалось очень близким: несколько более четырех двоичных единиц информации.
А такие "курьезы", такие точные характеристики очень важны для создания словарей машинного перевода, для преподавания иностранных языков, даже для выяснения некоторых вопросов в экспериментальной психологии. И уж конечно, для изучения поэтического творчества.
Выдающийся советский математик академик А. Н. Колмогоров проанализировал, например, соотношение запаса слов с рифмой. Из какого количества слов можно получить те или иные сочетания рифм? Оказалось, 10 слов для выбора одной рифмующейся пары -очень мало. При 20 словах выбор одной рифмы тоже ненадежен. А вот зал ас в 100 слов дает уже тройную рифму. 200 слов дают возможность найти четырехкратную рифму. Значит, при 200 словах можно писать сонеты. 500 слав - запас, который в изобилии дает поэтам десятикратные рифмы. Подсчитали и "взаимоотношение" букв в словах. Если бы все комбинации букв были возможны, то из 30 букв можно составить 30 одно-буквенных слов. Двубуквенных - 302 - было бы уже 900. 303 дали бы 27 000 трехбуквенных слов. 304 равно 810 000 слов четырехбуквенных и т. д. А язык содержит примерно 50 тысяч наиболее употребительных слов. Если принять среднее число букв в слове за семь, то окажется, что только 0,0002% всех возможных комбинаций букв являются словами. И буквы в словах появляются неравномерно. С этой целью исследовали разнообразные тексты. Для русского языка, например, была установлена такая частота повторения: А - 6,2%, О - 9%, И - 6,2%, Н - 5,3%, Ю -0,6% и т. д.
По вероятностным появлениям всех букв можно подсчитать "информационную нагрузку" каждой буквы. Интересно, что в романе "Евгений Онегин" такая "нагрузка" оказалась равной 0,4. Анализ же стихов поэта "средних способностей" дал совершенно другой результат: "информационная нагрузка" буквы в стихах была 0,18 - в 2,2 раза меньше. Как видите, даже чисто математические исследования творчества Пушкина показали гениальность русского поэта: высокую информационную насыщенность его произведений.
Результаты подобных исследований, проводимых лингвистами-математиками, представляют собой большой интерес и для "собственно лингвистов", изучающих тот или иной язык, и для литературоведов, исследующих, как писатели используют язык, каковы особенности их творчества.
Математическая лингвистика, основываясь на статистическом анализе структуры языка, использует для моделирования языка и электронно-вычислительные машины. Именно к таким моделям "операций, которые человек осуществляет над языком", относятся "литературные способности" электронных машин.

Это не хаотическое нагромождение букв. Величина букв русского алфавита на рисунке соответствует их относительной частоте в текстах, а следовательно, вероятности их появления
* * *
Как машина пишет?
На основе статистического анализа языка машина "научилась" осуществлять синтез фразы. Значит, ей не будет стоить большого труда синтезировать - составить согласно программе - предложения из запаса слов, которые находятся в машинной "памяти". Действительно, какая разница машине - искать в "памяти" зашифрованную букву или зашифрованное слово?
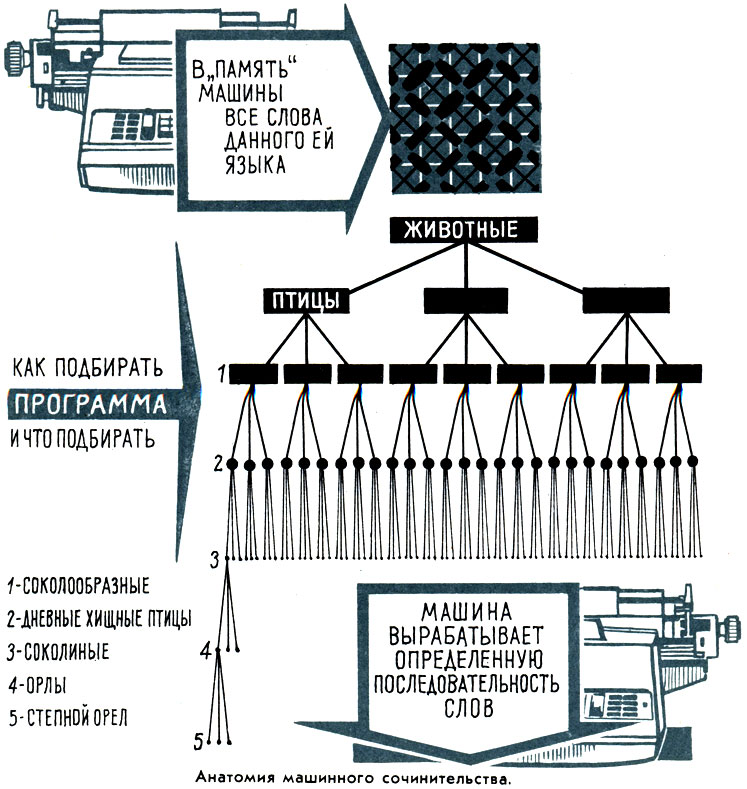
Анатомия машинного сочинительства
Для "литературного творчества" в машину можно вложить словарь, в котором родственные понятия будут записаны близкими кодами:
1001001 - животное,
1000100 - птица,
1001101 - орел и т. д.
Машина по программе и по этим кодам подберет близкие по смыслу слова. Основой "творчества" служит первоначальный текст, введенный в машину. Работа над созданием "литературного произведения" идет циклами. При каждом цикле повторения программы машина расширяет основной текст. Расширяя, отходит от него все дальше и дальше, но "в меру" - не искажает его до полной бессмысленности.
А дальше - процесс построения фраз. Все слова машина грамматически правильно собирает в предложения, используя команды программы.
* * *
В качестве справки: каково же машинное творчество - целое "собрание сочинений", написанных разными машинами за несколько последних лет.
Машина "RCA-301". "научилась" писать белые стихи. Словарный запас "поэта" - 130 слов. Размер стихов жестко задан. Машина пишет 150 четверостиший в минуту. Названий стихам не дает, а только нумерует их.
Стихотворение №027
Пока жизнь создает ошибочные, совершенно пустые образы,
Пока медленное время течет мимо полезных дел,
А звезды уныло кружатся в небе, Люди не могут смеяться.
Поэма № 929
Пока слепо плыл сон над разбитыми надеждами,
Космос с болью сочился над разбитой любовью.
Был из скрытых людей свет твой медленно изгнан,
И небо не спало.
А вот пример творчества "МУКа" - "электронного мозга" Манчестерского университета.
Любовное письмо
Мое маленькое сокровище! Моя вразумительная привязанность чудесно
привлекает твой ласковый восторг. Ты мое любящее обожание,
мое распирающее грудь обожание. Мое братское чувство с затаенным
дыханием ожидает твоего дорогого нетерпения. Обожание моей любви
нежно хранит твой алчный пыл.
Твой тоскующий МУК.
Другой автор - французская вычислительная машина "Калиоппа".
Отрывок из рассказа
[Spoiler (click to open)]
Мой горизонт состоит лишь из красной портьеры, откуда с перерывами
исходит удушливая жара. Едва можно различить мистический силуэт женщины,
гордой и ужасной: эта знатная дама, должно быть, одно из времен года.
Кажется, она прощается. Я больше ничего не вижу и продвигаюсь к занавесу,
который мои руки судорожно раздвигают. Вот, по ту сторону, странный
трагический пейзаж: циветта скребет землю, птицы летают с обеих сторон,
садятся на ветви деревьев, наполовину иссохших. А тут и черепаха,
застывшая неподвижно: она почувствовала мое присутствие.
Но почему она покрыта инеем? Мальчик подбегает; его пухленькие руки,
его серьезное и смуглое лицо придают ему вид молодого героя.
Нетрудно догадаться, что в своем "творчестве" машины удивительно похожи на некоторых ультрамодных западных творцов формалистических произведений. Вероятно, не последнее место в этом занимает то обстоятельство, что программу для машин готовят люди, словарный запас подбирают они же. Короче, от машин-литераторов получают то, что хотят получить!
Как уже говорилось, статистический подход к языку - один из методов математической лингвистики. Другой - не менее интересный и не менее важный - сравнение естественных языков с искусственно построенными языками математической логики. Призвав в союзницы математическую статистику, теорию информации, теорию вероятностей и другие науки, математическая лингвистика создает новые, более гибкие, более простые искусственные языки для электронно-вычислительных машин.
И еще один инструмент исследования в этой области - так называемые анализирующие грамматические модели и модели порождающих грамматик. За этими устрашающими специальными названиями скрывается стремление математической лингвистики разработать модели языка для самых разных целей.
Для каких именно? Здесь придется сказать лишь о том, что сфера применения математической лингвистики широка: создание формальных языков машин, машинный перевод, дешифровка забытых письменностей и некоторые другие. Каждая из них - и увлекательна, и полна неожиданностей, и имеет практический интерес.
В этом убедят вас несколько конкретных примеров.
Именно математическая лингвистика определяет, как лучше осуществить машинный перевод с обычного языка, русского, английского или любого другого, на машинно-информационно-логический, каким только и умеет пользоваться машина. Математическая лингвистика работает и над проблемами записи человеческой речи для конструирования автоматических стенографов и читающих автоматов. Очень гуманна роль этой науки в области исследований, связанных с применением электронно-вычислительных машин для облегчения языкового общения людей, лишенных слуха и зрения.
Начало пути математической лингвистики многообещающе. Поэтому можно ожидать, что .и дальнейший ее путь, дальнейшее ее развитие будет успешным и плодотворным.

Источник: Слова и числа

Лингвистика математическая
Научная дисциплина, применяющая
математические методы Для исследования
языка и использующая электронные
вычислительные машины для моделирования
языка и тех операций, которые человек
осуществляет над языком.
Слова и числа
Пожалуй, до недавнего времени одной из самых "нематематических", самых описательных наук по праву считали лингвистику. А вот теперь говорят о лингвистике математической.
Подобно тому, как теория вероятностей произвела в физике переворот, так и введение в лингвистику вероятностных и количественных методов придало этой гуманитарной науке элементы строгости и точности.
Круг вопросов новой науки очень широк. Сначала познакомимся с одним интересным направлением - с количественным описанием языка.
По мнению специалистов, любой язык характеризуют некоторые простые количественные соотношения. Сколько слов в различных языках, каково различие между числом слов и числом морфем и фонем? Каково соотношение между словами и слогами, фонемами и морфемами?
[Spoiler (click to open)]
Вам не показались эти вопросы слишком "узкими", "вопросами ради вопросов"? Наверное, показались. Но математическое исследование языка - не забава для ученых, не досужее "буквоедство". Практическое значение такого подхода к языку очень велико. Именно количественные характеристики помогают определить природу, характер неизвестной письменности, помогают л ее дешифровке. Нужны они и для описания современных языков, для изучения их истории, для определения их родства.
Статистический подход к языку приводит иногда к поразительным результатам/Выяснилось, например, что у столь различных, с нашей точки зрения, языков, как русский, английский, самоанский, количество информации, приходящейся на букву "Н", оказалось очень близким: несколько более четырех двоичных единиц информации.
А такие "курьезы", такие точные характеристики очень важны для создания словарей машинного перевода, для преподавания иностранных языков, даже для выяснения некоторых вопросов в экспериментальной психологии. И уж конечно, для изучения поэтического творчества.
Выдающийся советский математик академик А. Н. Колмогоров проанализировал, например, соотношение запаса слов с рифмой. Из какого количества слов можно получить те или иные сочетания рифм? Оказалось, 10 слов для выбора одной рифмующейся пары -очень мало. При 20 словах выбор одной рифмы тоже ненадежен. А вот зал ас в 100 слов дает уже тройную рифму. 200 слов дают возможность найти четырехкратную рифму. Значит, при 200 словах можно писать сонеты. 500 слав - запас, который в изобилии дает поэтам десятикратные рифмы. Подсчитали и "взаимоотношение" букв в словах. Если бы все комбинации букв были возможны, то из 30 букв можно составить 30 одно-буквенных слов. Двубуквенных - 302 - было бы уже 900. 303 дали бы 27 000 трехбуквенных слов. 304 равно 810 000 слов четырехбуквенных и т. д. А язык содержит примерно 50 тысяч наиболее употребительных слов. Если принять среднее число букв в слове за семь, то окажется, что только 0,0002% всех возможных комбинаций букв являются словами. И буквы в словах появляются неравномерно. С этой целью исследовали разнообразные тексты. Для русского языка, например, была установлена такая частота повторения: А - 6,2%, О - 9%, И - 6,2%, Н - 5,3%, Ю -0,6% и т. д.
По вероятностным появлениям всех букв можно подсчитать "информационную нагрузку" каждой буквы. Интересно, что в романе "Евгений Онегин" такая "нагрузка" оказалась равной 0,4. Анализ же стихов поэта "средних способностей" дал совершенно другой результат: "информационная нагрузка" буквы в стихах была 0,18 - в 2,2 раза меньше. Как видите, даже чисто математические исследования творчества Пушкина показали гениальность русского поэта: высокую информационную насыщенность его произведений.
Результаты подобных исследований, проводимых лингвистами-математиками, представляют собой большой интерес и для "собственно лингвистов", изучающих тот или иной язык, и для литературоведов, исследующих, как писатели используют язык, каковы особенности их творчества.
Математическая лингвистика, основываясь на статистическом анализе структуры языка, использует для моделирования языка и электронно-вычислительные машины. Именно к таким моделям "операций, которые человек осуществляет над языком", относятся "литературные способности" электронных машин.

Это не хаотическое нагромождение букв. Величина букв русского алфавита на рисунке соответствует их относительной частоте в текстах, а следовательно, вероятности их появления
* * *
Как машина пишет?
На основе статистического анализа языка машина "научилась" осуществлять синтез фразы. Значит, ей не будет стоить большого труда синтезировать - составить согласно программе - предложения из запаса слов, которые находятся в машинной "памяти". Действительно, какая разница машине - искать в "памяти" зашифрованную букву или зашифрованное слово?

Анатомия машинного сочинительства
Для "литературного творчества" в машину можно вложить словарь, в котором родственные понятия будут записаны близкими кодами:
1001001 - животное,
1000100 - птица,
1001101 - орел и т. д.
Машина по программе и по этим кодам подберет близкие по смыслу слова. Основой "творчества" служит первоначальный текст, введенный в машину. Работа над созданием "литературного произведения" идет циклами. При каждом цикле повторения программы машина расширяет основной текст. Расширяя, отходит от него все дальше и дальше, но "в меру" - не искажает его до полной бессмысленности.
А дальше - процесс построения фраз. Все слова машина грамматически правильно собирает в предложения, используя команды программы.
* * *
В качестве справки: каково же машинное творчество - целое "собрание сочинений", написанных разными машинами за несколько последних лет.
Машина "RCA-301". "научилась" писать белые стихи. Словарный запас "поэта" - 130 слов. Размер стихов жестко задан. Машина пишет 150 четверостиший в минуту. Названий стихам не дает, а только нумерует их.
Стихотворение №027
Пока жизнь создает ошибочные, совершенно пустые образы,
Пока медленное время течет мимо полезных дел,
А звезды уныло кружатся в небе, Люди не могут смеяться.
Поэма № 929
Пока слепо плыл сон над разбитыми надеждами,
Космос с болью сочился над разбитой любовью.
Был из скрытых людей свет твой медленно изгнан,
И небо не спало.
А вот пример творчества "МУКа" - "электронного мозга" Манчестерского университета.
Любовное письмо
Мое маленькое сокровище! Моя вразумительная привязанность чудесно
привлекает твой ласковый восторг. Ты мое любящее обожание,
мое распирающее грудь обожание. Мое братское чувство с затаенным
дыханием ожидает твоего дорогого нетерпения. Обожание моей любви
нежно хранит твой алчный пыл.
Твой тоскующий МУК.
Другой автор - французская вычислительная машина "Калиоппа".
Отрывок из рассказа
[Spoiler (click to open)]
Мой горизонт состоит лишь из красной портьеры, откуда с перерывами
исходит удушливая жара. Едва можно различить мистический силуэт женщины,
гордой и ужасной: эта знатная дама, должно быть, одно из времен года.
Кажется, она прощается. Я больше ничего не вижу и продвигаюсь к занавесу,
который мои руки судорожно раздвигают. Вот, по ту сторону, странный
трагический пейзаж: циветта скребет землю, птицы летают с обеих сторон,
садятся на ветви деревьев, наполовину иссохших. А тут и черепаха,
застывшая неподвижно: она почувствовала мое присутствие.
Но почему она покрыта инеем? Мальчик подбегает; его пухленькие руки,
его серьезное и смуглое лицо придают ему вид молодого героя.
Нетрудно догадаться, что в своем "творчестве" машины удивительно похожи на некоторых ультрамодных западных творцов формалистических произведений. Вероятно, не последнее место в этом занимает то обстоятельство, что программу для машин готовят люди, словарный запас подбирают они же. Короче, от машин-литераторов получают то, что хотят получить!
Как уже говорилось, статистический подход к языку - один из методов математической лингвистики. Другой - не менее интересный и не менее важный - сравнение естественных языков с искусственно построенными языками математической логики. Призвав в союзницы математическую статистику, теорию информации, теорию вероятностей и другие науки, математическая лингвистика создает новые, более гибкие, более простые искусственные языки для электронно-вычислительных машин.
И еще один инструмент исследования в этой области - так называемые анализирующие грамматические модели и модели порождающих грамматик. За этими устрашающими специальными названиями скрывается стремление математической лингвистики разработать модели языка для самых разных целей.
Для каких именно? Здесь придется сказать лишь о том, что сфера применения математической лингвистики широка: создание формальных языков машин, машинный перевод, дешифровка забытых письменностей и некоторые другие. Каждая из них - и увлекательна, и полна неожиданностей, и имеет практический интерес.
В этом убедят вас несколько конкретных примеров.
Именно математическая лингвистика определяет, как лучше осуществить машинный перевод с обычного языка, русского, английского или любого другого, на машинно-информационно-логический, каким только и умеет пользоваться машина. Математическая лингвистика работает и над проблемами записи человеческой речи для конструирования автоматических стенографов и читающих автоматов. Очень гуманна роль этой науки в области исследований, связанных с применением электронно-вычислительных машин для облегчения языкового общения людей, лишенных слуха и зрения.
Начало пути математической лингвистики многообещающе. Поэтому можно ожидать, что .и дальнейший ее путь, дальнейшее ее развитие будет успешным и плодотворным.

Источник: Слова и числа