Головной мозг vs. Нейросети. Биотехнологии будущего (окончание)

Мировая экономика становится все более «оцифрованной» благодаря многочисленным новым системам информационных технологий, основанным на искусственном интеллекте и машинном обучении - нейросетям. Эти технологии позволяют существенно повысить эффективность производственных процессов, но, если судить по статистическим данным, не ускоряют рост производительности в экономике: наоборот, за последние 4 года наметилась стагнация. Это так называемый современный парадокс производительности (подробнее см. https://econs.online/articles/opinions/iskusstvennyy-intellekt-i-paradoks-proizvoditelnosti/). В исследованиях головного мозга, напротив, наблюдается существенный прорыв, однако нейробиология по-прежнему не способна хоть как-то повлиять на усовершенствование механизмов современных нейросетей. Почему так? Ведь доказано, что принципы работы нейросети сходны с механизмом работы нейронов головного мозга.
Возможно, развязка кроется в самом подходе к конструированию нейросети - ведь вопрос о том, сколько наблюдений нужно иметь для обучения любой нейросети, часто оказывается непростым. Существует ряд правил, увязывающих число необходимых наблюдений с размерами сети (простейшее из них гласит, что число наблюдений должно быть в десять раз больше числа связей в сети). На самом деле это число зависит также от (заранее неизвестной) сложности того отображения, которое нейронная сеть стремится воспроизвести. С ростом количества переменных количество требуемых наблюдений растет нелинейно, так что уже при довольно небольшом (например, пятьдесят) числе переменных может потребоваться огромное число наблюдений. Эта трудность известна как "проклятие размерности" (подробнее см. http://statsoft.ru/home/textbook/modules/stneunet.html).
Если же наблюдать за активностью здорового мозга, то мы не увидим никаких лишних нейронов, каждый нейрон будет задействован, в разной степени, и конечно, каждому будет присвоена своя роль. Каким же образом это делает мозг, и каким должен быть алгоритм нейрона, чтобы это происходило, при низкой эффективности отдельно взятого нейрона?
Парадокс эффективности нейрона можно объяснить тем, что при увеличении количества нейронов в нервной системе уменьшается «внимание» процессов эволюции к отдельным нейронам. Поэтому нейроны кольчатого червя, можно выразиться, работают как часы, очень точно, нейроны же виноградной улитки и человека такой точностью похвастаться не могут, в их работе можно увидеть и спонтанную активность так и отсутствие ответа там, где он должен быть, так и его нестабильность. Чем же обусловлены такие значительные отличия?
Итак, сложной активности нейрона можно сопоставить две теории:
1) нейрон - это сложный вычислитель, алгоритм работы которого сложно понять и обосновать, либо
2) нейрон просто работает очень нестабильно, что компенсируется его избыточным количеством, что является самым простым решением с точки зрения эволюции. Примените к этим теориям правило бритвы Оккама, согласно которой нужно отставить идеи, которые имеют самое простое объяснение, и, вероятнее всего, эти идеи будут верными (подробнее о «бритве Оккама» тут: https://lana-artifex.livejournal.com/2955.html).
С одной стороны, парадокс эффективности нейрона даёт нам позитивную надежду, что необходимых вычислительных мощностей для моделирования мозга потребуется значительно меньше, чем при прямой оценке по количеству нейронов и синапсов в мозге человека. С другой стороны, это очень сильно усложняет изучение биологического мозга. Мы можем создать достаточно подробную модель небольшого фрагмента коры мозга, затратив большие вычислительные мощности, и в этой модели не увидеть каких-либо значимых процессов, которые указывали бы на то, как протекают когнитивные механизмы в нервной системе. Такие попытки уже неоднократно проводились.
На первый взгляд, самый простой и прямолинейный подход в создании общей теории работы мозга - это создание подробной модели мозга, в соответствии с множеством научных фактов известных о нейроне и синапсах. Моделирование - это самый практичный научный инструмент в изучении каких-либо сложных систем. Модель буквально раскрывает суть изучаемого объекта, позволяет погружаться и влиять на внутренние процессы, протекающие в моделируемой системе, давая возможность их глубже понимать.
У нейрона нет никаких исключительных органелл, которые производили бы вычисления, но его мембрана имеет ряд особенностей, и позволяют выполнять нейрону определённую работу. Это работу можно определить с помощью системы уравнений, называемой моделью Ходжкина-Хаксли, которая была разработана в 1952 году, за что её авторы получили нобелевскую премию.
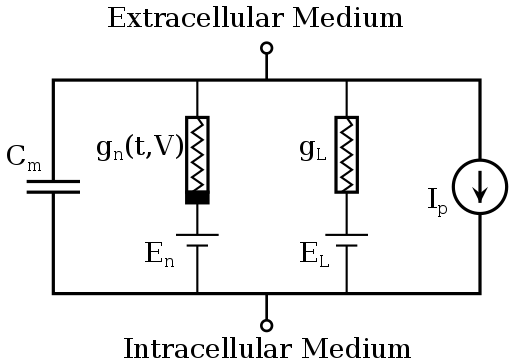
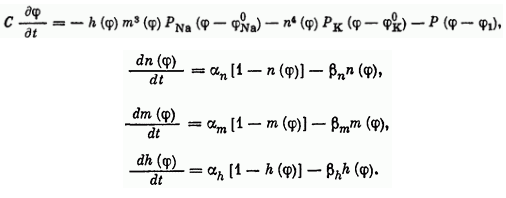
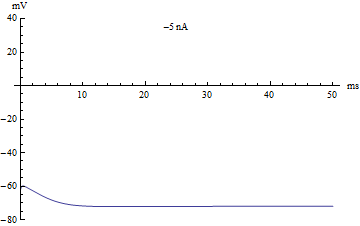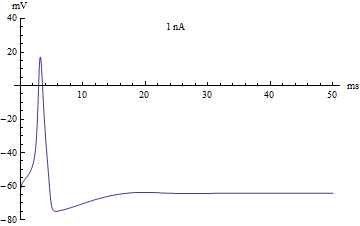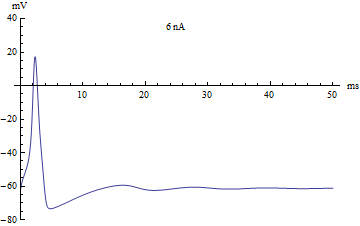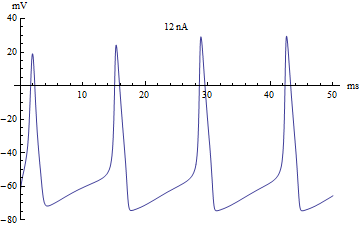
Эти на первый взгляд головоломные формулы содержат несколько коэффициентов, определяющих некоторые параметры мембраны нейрона, такие как скорость реакции ионных каналов, их проводимость и т.д. Эта волшебная модель описывает сразу несколько явлений, помимо изменения заряда на поверхности мембраны нейрона.
Во-первых, она описывает функцию активации нейрона, или механизм суммации, он достаточно прост. - Если исходный заряд недостаточен, то модель остаётся в равновесном состоянии. Если же заряд переходит через определённый порог, то модель отвечает одним спайком. Если заряд в значительной степени превышает данный порог, то модель отвечает серией спайков. В компьютерных нейронных сетях используется большое разнообразие вариантов функции активации, самой близкой к биологии может являться функция Хевисайда (единичная ступенька) и линейный выпрямитель (Rectifier). Но нужно понимать, что мы описываем достаточно простой аспект работы нейрона - суммацию.
Можно применить очень простой вариант модели суммации, который образно можно представить в виде сосуда, накапливающего в себе фактор побудительного воздействия. В случае если этот фактор превышал определённый порог, то нейрон активизировался. Чтобы этот сумматор работал в реальном времени, из образного сосуда фактор воздействия медленно истекал.

Эта модель суммации позволяла производить суммацию сигналов, которые приходили на нейрон асинхронно, и она достаточно реалистично работает. На мой взгляд, чем проще описывать этот процесс, тем лучше, и это непринципиальное отличие биологических и компьютерных сетей.
Во-вторых, модель Ходжкина-Хаксли описывает изменение заряда в одной точке мембраны, но если мы, к примеру, создадим топологически точную 3D модель нейрона и разобьём эту модель на равномерную сетку, мы сможем применить модель Ходжкина-Хаксли в каждой вершине (узле) этой сетки, с условием влияния заряда на значение в соседних вершинах по сетке. Тем самым мы получим модель распространения возбуждения по нейрону близко к тому, как это происходит в живом нейроне.
Главные выводы, которые можно сделать из этой модели, это то, что возбуждение, возникнув на любом участке мембраны, распространяется на всю мембрану, в том числе распространяется по длинному аксону к самым удалённым синапсам. Модель Ходжкина-Хаксли очень ресурсозатратна, поэтому для целей моделирования используют менее затратные модели с очень схожими графиками, таких придумано сразу несколько моделей.
В рамках проекта Human Brain Project (https://ru.wikipedia.org/wiki/Human_Brain_Project) была создана модель небольшого фрагмента коры мозга мыши, при это м её создатели учли очень многое. -
3D модели нейронов были воссозданы по реальным нейронам, использовался один из вариантов моделей Ходжкина-Хаксли, учитывались различные типы нейронов и нейромедиаторов, и нет сомнений в том, что модель действительно соответствует биологическому аналогу. На это потрачено множество ресурсов и времени, но так и не дало значимых результатов по причине того, что в столь малом размере из-за парадокса эффективности нейрона невозможно было увидеть сколько-нибудь значимых процессов. Поэтому путь подробного повторения биологии является очень и очень трудоёмким. Залог успеха - это прежде всего, возможность понимания того, как работает нервная ткань и нейроны в более широком масштабе.
Давайте теперь рассмотрим то, как мозг обрабатывает информацию на частном примере, - а именно на обработке зрительной информации. Мы составим схему нейронной сети, выполняющей эту задачу.

Информация с сетчатки глаза по зрительному нерву передаётся в таламус, там информация практически не подвергается значимым преобразованиям. Далее она передается в первичную зрительную зону коры головного мозга (V1). В коре головного мозга выделяют шесть слоёв, но эти слои делятся по гистологическим или морфологическим признакам.

Вероятно, в схеме данной нейросети мы имеем дело с двумя слоями, так как некоторые структуры повторяются дважды. Но и при этом мы имеем дело скорее не с двумя отдельными самостоятельными слоями, а, скорее, со слоями нервных клеток, работающих в тандеме.
Охарактеризуем зону зрительной коры V1 как первый слой, в котором происходит обработка информации. Зона V1 также имеет обратные связи с таламусом. Подобные обратные связи имеются и между всеми последующими слоями. Эти связи формируют циклические передачи возбуждения между слоями, называемыми реверберациями.
После зоны V1 информация передаётся в следующую зону V2, все последующие зоны будут иметь меньшие площади. В зависимости от того, что наблюдает мозг, - был ли это объект, символ, лицо человека, место или что-то другое, - информация из V2 может передаваться в различные области V3, V4, V5. То есть уже на этой зрительной области V2 происходит серьёзная категоризация зрительных образов. И примерно уже на третьем или четвёртом слое можно будет выделить нейроны-детекторы определённых образов. К примеру, мы сможем выделить нейрон-детектор буквы «А», цифры 3 или лица Дженнифер Энистон:)). По активации этих нейронов-детекторов мы сможем судить об том, что именно в данный момент наблюдает мозг.
Это достаточно простая архитектура биологической нейросети, если сравнить её с архитектурой компьютерных нейросетей, специализированных на распознавании визуальных образов (так называемых «свёрточных» нейронных сетей).
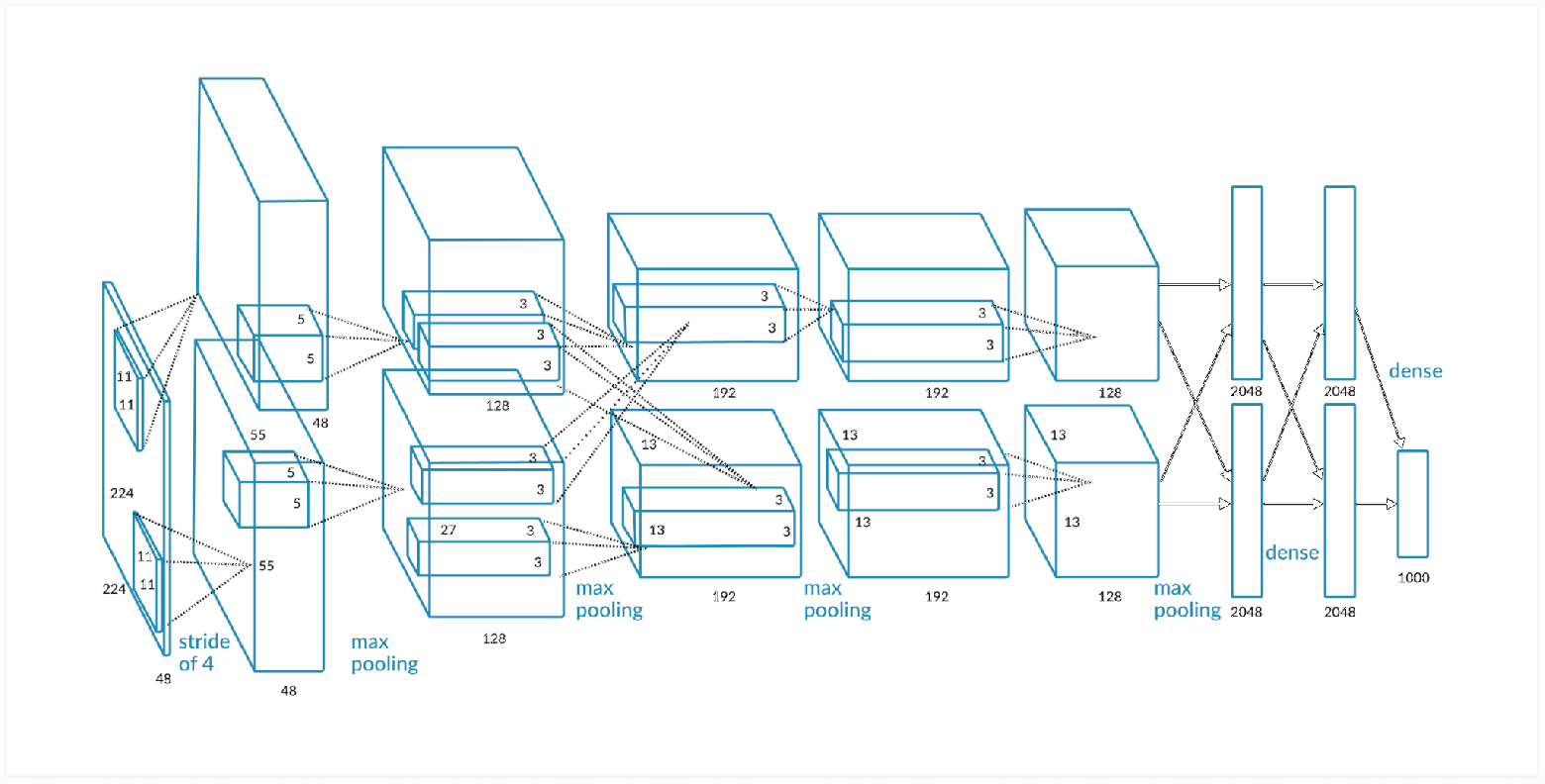
AlexNet - свёрточная нейронная сеть для классификации изображений
Есть схожие моменты в обеих нейросетях, - это иерархия свёрточных слоёв, т.е. каждый последующий слой будет иметь всё меньшее количество параметров. Но у слоёв данного типа компьютерных сетей нет рекуррентных связей, и конечно, их наличие не является критерием для успешного распознавания образов, так как природа ревербераций в живом мозге до конца не изучена. Есть гипотеза, что реверберации связаны с явлением моментальной памяти, той памяти, которая позволяет нам, к примеру, не сбиться при наборе номера телефона или его произношении. Реверберирующая активность как бы задерживается, обозначая участки, по которым проходит эта активность, тем самым создается контекст обрабатываемой информации.
Человек может распознать сложные образы за доли секунды, скорость распространения потенциала действия по мембране - от 1 до 120 м/с, синаптическая задержка в химических синапсах составляет 0,2-0,5мс, что говорит о том, что за время распознавания может задействоваться цепочка не более чем ста нейронов.
Вышеописанное говорит о том, что в нашей черепной коробке присутствует нейронная сеть, работающая быстрее и эффективнее любой компьютерной нейронной сети, при этом организованна она относительно просто, и выполняет относительно несложные преобразования информации. Понимание этого и подстрекает учёных производить поиск алгоритма сети, который бы выполнял задачу распознавания образов с применением значительно меньших вычислительных ресурсов, чем современные нейронные сети. При этом также нужно помнить о параметрах, которые нужно выбрать при обучении такой нейросети. Но это уже тема для большой научной статьи, не в рамках этого блога.
По материалам научно-популярных книг о нейробиологии и квантовой механике: С. Ллойд («Программируя Вселенную»), С. Доронин («Квантовая магия»)