порядок рождения
Скотт Александр, автор широко известного в узких кругах гиковского блога про психологию-политику-философию, провел подробный опрос читателей, на который ответили семь тысяч человек, и обнаружил очень сильный эффект порядка рождения: напр., если взять всех читателей, у которых есть ровно 1 брат или сестра, то среди них у 71% этот брат или сестра младшая. Вдумайтесь: не у половины из них, а почти у трех четвертей!! Вот запись Скотта: http://slatestarcodex.com/2018/01/08/fight-me-psychologists-birth-order-effects-exist-and-are-very-strong/. Я поверить в такой сильный эффект не мог, решил, что тут какая-то ошибка, скачал данные и проверил сам:
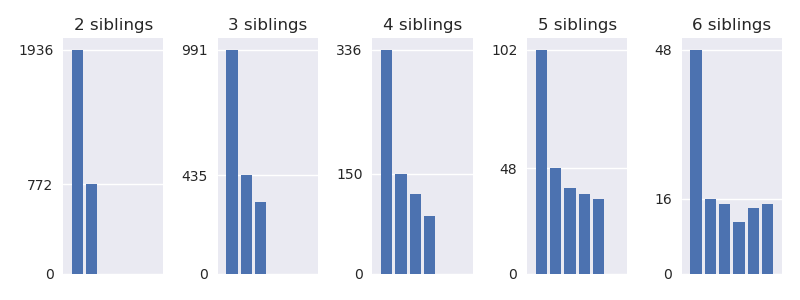
На левой панели кол-во старших и младших читателей в семьях из двух детей, потом кол-во старших, средних и младших в семьях из трех, и т.д. Но может быть, тут какой-то странный эффект возраста (напр., большинству читателей 20 лет и их младшие братья/сестры еще не доросли)? Нет, вот как выглядит процент по возрастам (и заодно по полам):
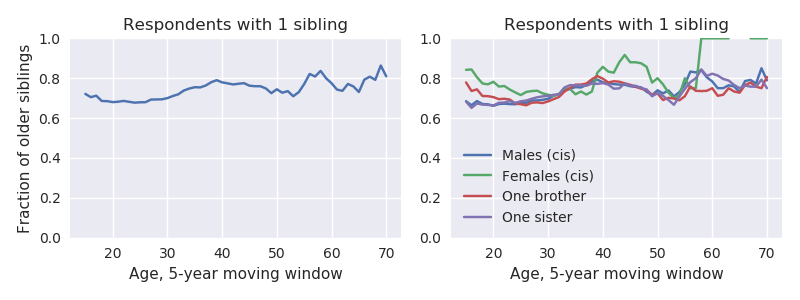
Я постулировал простенькую модель, в которой шансы быть читателем Скотта экспоненциально падают с номером рождения, и зафитил ее с помощью maximum likelihood (используя биномиальные likelihoods) к данным по семьям всех размеров. Вот что получилось:
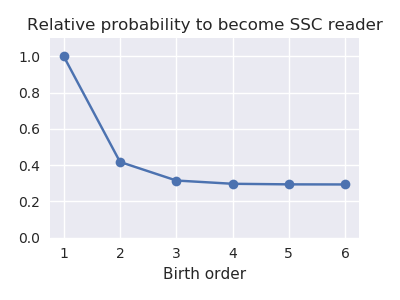
У второго ребенка шансы примерно 0.4, асимптота получается примерно 0.3. Т.е. вероятность, что старший ребенок окажется читателем Скотта превышает в ДВА С ПОЛОВИНОЙ раза эту вероятность для остальных детей. Как такое вообще может быть?
Если посмотреть литературу, то, оказывается, эффект birth order на IQ довольно надежно установлен: у старших детей IQ в среднем выше. Но этот эффект ничтожен: по разным оценкам, разницы между первым и вторым ребенком от d=0.1 до d=0.2, т.е. в среднем разница в 2-3 пункта IQ при стандарнтном отклонении в 15 пунктов. (Согласно последней статье в списке, эффект обусловлен не порядком рождения как таковым, а кол-вом старших братьев/сестер не умерших в младенчестве, т.е. если старший ребенок быстро умер, то повышенный IQ в среднем будет у второго, и т.д.; см. картинку.)
http://science.sciencemag.org/content/182/4117/1096
http://www.sciencedirect.com/science/article/pii/S0160289607000062
http://science.sciencemag.org/content/316/5832/1717

Предположим, что эффект составляет d=0.2. Предположим также, что читателями Скотта становятся люди с IQ>130, т.е. с z>2 (оценка кажется разумной). Тогда шансы второго ребенка должны составлять примерно 0.6 от шансов первого -- довольно существенный эффект (важно понимать, что очень небольшая разница в среднем может привести к большой разнице в хвосте распределения), но все-таки далеко не 0.4. Даже при отсеве в z>3, что уже малоправдоподобно, получается всего 0.53. Чтобы получить 0.4, никакого отсева не хватит, и нужно предположить как минимум эффект в d=0.5, а это гораздо выше, чем показывают имеющиеся данные.
Удивительно.

На левой панели кол-во старших и младших читателей в семьях из двух детей, потом кол-во старших, средних и младших в семьях из трех, и т.д. Но может быть, тут какой-то странный эффект возраста (напр., большинству читателей 20 лет и их младшие братья/сестры еще не доросли)? Нет, вот как выглядит процент по возрастам (и заодно по полам):

Я постулировал простенькую модель, в которой шансы быть читателем Скотта экспоненциально падают с номером рождения, и зафитил ее с помощью maximum likelihood (используя биномиальные likelihoods) к данным по семьям всех размеров. Вот что получилось:

У второго ребенка шансы примерно 0.4, асимптота получается примерно 0.3. Т.е. вероятность, что старший ребенок окажется читателем Скотта превышает в ДВА С ПОЛОВИНОЙ раза эту вероятность для остальных детей. Как такое вообще может быть?
Если посмотреть литературу, то, оказывается, эффект birth order на IQ довольно надежно установлен: у старших детей IQ в среднем выше. Но этот эффект ничтожен: по разным оценкам, разницы между первым и вторым ребенком от d=0.1 до d=0.2, т.е. в среднем разница в 2-3 пункта IQ при стандарнтном отклонении в 15 пунктов. (Согласно последней статье в списке, эффект обусловлен не порядком рождения как таковым, а кол-вом старших братьев/сестер не умерших в младенчестве, т.е. если старший ребенок быстро умер, то повышенный IQ в среднем будет у второго, и т.д.; см. картинку.)
http://science.sciencemag.org/content/182/4117/1096
http://www.sciencedirect.com/science/article/pii/S0160289607000062
http://science.sciencemag.org/content/316/5832/1717

Предположим, что эффект составляет d=0.2. Предположим также, что читателями Скотта становятся люди с IQ>130, т.е. с z>2 (оценка кажется разумной). Тогда шансы второго ребенка должны составлять примерно 0.6 от шансов первого -- довольно существенный эффект (важно понимать, что очень небольшая разница в среднем может привести к большой разнице в хвосте распределения), но все-таки далеко не 0.4. Даже при отсеве в z>3, что уже малоправдоподобно, получается всего 0.53. Чтобы получить 0.4, никакого отсева не хватит, и нужно предположить как минимум эффект в d=0.5, а это гораздо выше, чем показывают имеющиеся данные.
Удивительно.