Math Education
According to this morning's paper (or it might have been yesterday's -- I read articles from both days this morning), 40% of students entering college (nationally) are placed into remedial courses for English or math. Forty. Percent. That's HUGE!
(...although it does help to explain why students were so ill-prepared for precalculus last fall...)
Checking the course listings for this fall at MV, and after some quick math (quick enough that I didn't re-count to make sure I didn't double count, etc.), around 42% of the sections offered in math this fall (excluding online & hybrid courses) are remedial math courses (MA045 & MA050 -- combined, there are 37 sections of these classes being taught). These courses meet five hours a week and are non-credit bearing. A vast majority of these classes have wait-lists or are full. (course listings)
There are various reasons for there to be a high number of students at a community college in particular taking remedial classes (for example, there's a higher number of returning students who haven't taken math in several years), but "the vast majority of students who take remedial courses in college do so to gain the skills and knowledge they should have gotten in high school and which are necessary for them to succeed in 'regular' college classes" (Paying Double, page 2). In other words, high schools are not doing an effective job of giving students a solid foundation in math.
A report sponsored by the Carnegie Foundation has this to say about how math is taught in our schools:
Although our focus here is on the community college students, it is important to
acknowledge that the methods used to teach mathematics in K-12 schools are not
succeeding, and that the limitations of students' mathematical proficiency are cumulative and
increasingly obvious over time.
The limitations in K-12 teaching methods have been well-documented in the research
literature. The Trends In International Mathematics and Science Study (TIMSS) video
studies (Stigler & Hiebert, 1999; Hiebert et al., 2003) showed that the most common
teaching methods used in the U.S. focus almost entirely on practicing routine procedures
with virtually no emphasis on understanding of core mathematics concepts that might help
students forge connections among the numerous mathematical procedures that make up the
mathematics curriculum in the U.S. The high-achieving countries in TIMSS, in contrast, use
instructional methods that focus on actively engaging students with understanding
mathematical concepts. Procedures are taught, of course, but are connected with the
concepts on which they are based. In the U.S., procedures are more often presented as step-by-
step actions that students must memorize, not as moves that make sense mathematically.
Given that U.S. students are taught mathematics as a large number of apparently unrelated
procedures that must be memorized, it is not surprising that they forget most of them by the
time they enter the community college. It is true that some students figure out on their own
that mathematics makes sense and that procedures forgotten can be reconstructed based on
a relatively small number of core concepts. And even a few students who don't figure this
out are smart enough to actually remember the procedures they are taught in school. But
many students don't figure this out, and these are the ones that swell the ranks of students
who fail the placement tests and end up in developmental mathematics.
--Stigler et. al., page 3
Yes! Yes! Yes! This is exactly the way I approach math: understanding the why you do the steps you do in math will not only help you remember what to do, but also better enable you to generalize to a new problem later on. I've met with opposition on this philosophy by Experienced Math Teachers, saying that some students can't learn the "why" and don't need to in order to do whatever it is they're going to be doing in the future. Maybe I'm not experienced enough to be bitter, but I disagree. I think students want to understand math but are frustrated that they "don't get it." It's like...let's say you're baking and all you do is memorize recipes. Then sure, you can bake a cake. But suppose you're now told to create your own cake. If you don't know what ingredients are important to the rising process or the flavor or the texture and so on, then you're limited only to the one cake you know how to bake and you can never grow. Understanding the chemical responses is more difficult than memorizing the recipes, but if you're to be successful at baking, you need to know at least the basics. Similarly, if you're to be successful at math, you need to have a fundamental understanding of why things work the way they do.
(I only skimmed a bit of the quoted article (and intend to read it all later), but it's encouraging to know that I'm not alone in this line of thinking. After hearing stuff this year from others who've been in the biz longer than I, I was beginning to think perhaps I was a foolish young optimist. At least now I know there are a handful of foolish older optimists as well ^__^)
Meanwhile, there are also those students that say, "But I got A's in high school -- how can I be failing now?" According to a study done in 2008 by the Strong American Schools, "nearly four out of five remedial students had a high school GPA of 3.0 or higher." (CNSNews.com) When schools with better results get more state funding, it's only natural that grades are going to be inflated. Unfortunately, what results is an overall poor assessment of student learning, which is now leading to poor preparedness for college. However, new data suggests that the problem of grade-inflation may not necessarily originate in high school.
One of the larger puzzles in NY education over the past few years is determining why students in elementary school score well on state exams in English and math, but then by the time students reach middle school or high school, scores drop considerably. Apparently, the Utica OD reports, that there's been some "tougher grading" on state exams in 2010 than in 2009, which has lead to fewer students passing. In other words, the state has changed the guidelines regarding how state exams are to be graded to be more rigorous in 2010. And the difference in scores is staggering.
For example, the average percent of students in Oneida County that passed the state math exam in 2009 was 90.3%. Compare that to a passing rate of 61.3% in 2010. Additionally, of the 14 schools that reported a passing success rate of 100% in 2009, half of them reported a passing success rate of 60% or less in 2010.
Although the difference is incredible, I think the "tougher" grading may just be a more accurate assessment. Now, I don't know much about the exams or how they were changed or how the grading was made "tougher" but if the average passing rate of 3rd-to-8th-graders is actually 61.3%, that means that 38.7% of students that age are or should be in remedial classes. The 40% of college students enrolled in remedial courses, then, is not so much a surprise if students as far back as 3rd grade are not being accurately assessed.
Because I've always been interested in this sort of stuff, I constructed some tables using the data from the OD (which you can find here). I looked at only Oneida County schools (because of the way the data's reported, I had to retype it all in Excel to be able to work with it, so I figured I'd limit myself to just one county) and the students being assessed are in grades 3 through 8. I also combined some of the info with data from the New York Schools website.
And now, witness the result of a morning of number crunching & HTML tables!
Average percent of Oneida County students that passed
the state math
exam in 2009 and 2010 (by grade level)
3rd Grade
4th Grade
5th Grade
6th Grade
7th Grade
8th Grade
2009
94.0
87.8
91.0
87.0
93.5
86.8
2010
58.3
63.5
61.5
60.9
65.4
59.1
Average Percent of Students in Grades 3-8 Who Passed
the State Math Exam
in Oneida County (by school district)
School District
Total Number of
Students *
2009
2010
Adirondack Central
1,460
91.4%
51.7%
Camden Central
2,741
91.3%
66.3%
Clinton Central
1,511
91.9%
66.5%
Holland Patent Central
1,775
89.5%
57.3%
New Hartford Central
2,656
95.6%
74.4%
New York Mills Union Free
602
90.6%
70.7%
Oriskany Central
739
94.9%
58.8%
Remsen Central
567
88.8%
53.9%
Rome City
5,817
87.2%
51.2%
Sauquoit Valley Central
1,237
95.6%
71.6%
Utica City
9,041
82.2%
49.4%
Vernon-Verona-Sherrill City
2,372
94.5%
70.9%
Waterville Central
936
92.6%
63.1%
Westmoreland Central
1,106
90.4%
60.2%
Whitesboro Central
3,671
94.4%
74.3%
* This info comes
from the
New York Schools website.
Oneida County Schools with Biggest Difference
in % of Students
Passing from 2009 to 2010
Difference
School
District
Grade
-70.6
Forestport Elementary
Adirondack Central
3
-58.2
Stokes Elementary
Rome City
3
-56.9
Bellamy Elementary
Rome City
4
-56.1
North Bay Area
Camden Central
3
-53.7
Remsen
Remsen Central
3
-52.6
Martin Luther King Jr Elementary
Utica City
4
-52.3
Oriskany
Oriskany Central
3
-52.3
Sauquoit Valley
Sauquoit Valley Central
3
-52.2
Oriskany
Oriskany Central
8
-50.9
John E Joy Elementary
Rome City
3
Oneida County Schools with Smallest Difference
in % of Students
Passing from 2009 to 2010
Difference
School
District
Grade
-1.3
E A Mcallister Elementary
Vernon-Verona-Sherrill City
6
+2.1
Harts Hill School
Whitesboro Central
4
+2.9
North Bay Area
Camden Central
4
-4.9
E A Mcallister Elementary
Vernon-Verona-Sherrill City
4
-5.3
New York Mills
New York Mills Union Free
6
-6.7
New York Mills
New York Mills Union Free
4
-7.2
Thomas Jefferson Elementary
Utica City
5
-7.5
Sauquoit Valley
Sauquoit Valley Central
8
-7.9
Sauquoit Valley
Sauquoit Valley Central
4
-8.9
Hughes Elementary School
New Hartford Central
3
And, for the halibut, here's a scatter plot of district passing rates, to see if the 2009% passing rate and the 2010% passing rate were at all correlated. It would seem not very (r = 0.521)...
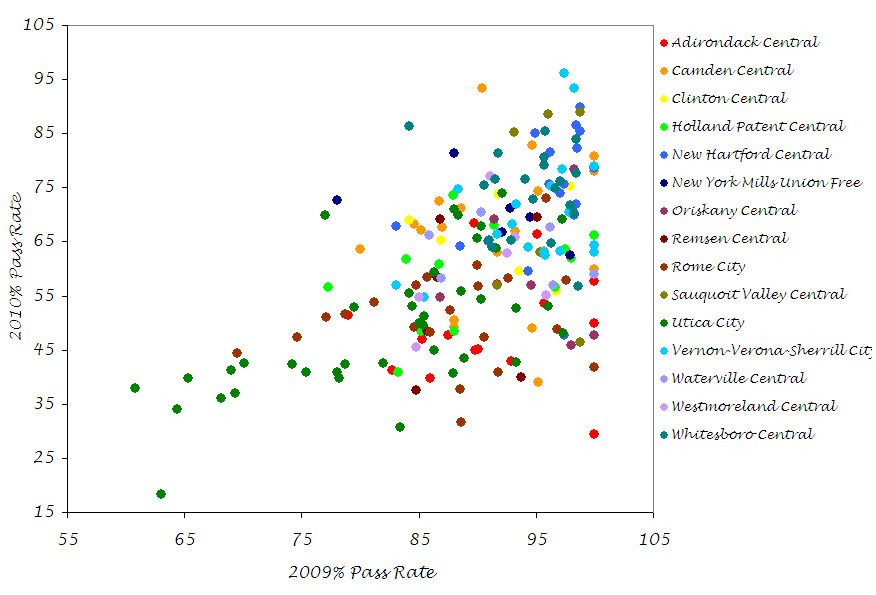
(click for full size image)
I find all this stuff fascinating anyway, but it's particularly appropriate since I'll be teaching remedial math this year. These are the courses I'm most concerned about because of the way they're taught, although I've also heard a rumor that they're thinking of changing that. Right now, my understanding is that things are fairly similar to the rigid old-school method described here (just under the "too many rules" subheading). It's definitely going to be an interesting semester, that's for sure.
On a related note, I guess you can tell what you're truly passionate about when you keep researching & writing through breakfast and lunch, and suddenly you discover it's 3:15pm when just a moment ago it was only a few minutes 'til 9:00am.
...I'm'a go find some food, I think...
(...although it does help to explain why students were so ill-prepared for precalculus last fall...)
Checking the course listings for this fall at MV, and after some quick math (quick enough that I didn't re-count to make sure I didn't double count, etc.), around 42% of the sections offered in math this fall (excluding online & hybrid courses) are remedial math courses (MA045 & MA050 -- combined, there are 37 sections of these classes being taught). These courses meet five hours a week and are non-credit bearing. A vast majority of these classes have wait-lists or are full. (course listings)
There are various reasons for there to be a high number of students at a community college in particular taking remedial classes (for example, there's a higher number of returning students who haven't taken math in several years), but "the vast majority of students who take remedial courses in college do so to gain the skills and knowledge they should have gotten in high school and which are necessary for them to succeed in 'regular' college classes" (Paying Double, page 2). In other words, high schools are not doing an effective job of giving students a solid foundation in math.
A report sponsored by the Carnegie Foundation has this to say about how math is taught in our schools:
Although our focus here is on the community college students, it is important to
acknowledge that the methods used to teach mathematics in K-12 schools are not
succeeding, and that the limitations of students' mathematical proficiency are cumulative and
increasingly obvious over time.
The limitations in K-12 teaching methods have been well-documented in the research
literature. The Trends In International Mathematics and Science Study (TIMSS) video
studies (Stigler & Hiebert, 1999; Hiebert et al., 2003) showed that the most common
teaching methods used in the U.S. focus almost entirely on practicing routine procedures
with virtually no emphasis on understanding of core mathematics concepts that might help
students forge connections among the numerous mathematical procedures that make up the
mathematics curriculum in the U.S. The high-achieving countries in TIMSS, in contrast, use
instructional methods that focus on actively engaging students with understanding
mathematical concepts. Procedures are taught, of course, but are connected with the
concepts on which they are based. In the U.S., procedures are more often presented as step-by-
step actions that students must memorize, not as moves that make sense mathematically.
Given that U.S. students are taught mathematics as a large number of apparently unrelated
procedures that must be memorized, it is not surprising that they forget most of them by the
time they enter the community college. It is true that some students figure out on their own
that mathematics makes sense and that procedures forgotten can be reconstructed based on
a relatively small number of core concepts. And even a few students who don't figure this
out are smart enough to actually remember the procedures they are taught in school. But
many students don't figure this out, and these are the ones that swell the ranks of students
who fail the placement tests and end up in developmental mathematics.
--Stigler et. al., page 3
Yes! Yes! Yes! This is exactly the way I approach math: understanding the why you do the steps you do in math will not only help you remember what to do, but also better enable you to generalize to a new problem later on. I've met with opposition on this philosophy by Experienced Math Teachers, saying that some students can't learn the "why" and don't need to in order to do whatever it is they're going to be doing in the future. Maybe I'm not experienced enough to be bitter, but I disagree. I think students want to understand math but are frustrated that they "don't get it." It's like...let's say you're baking and all you do is memorize recipes. Then sure, you can bake a cake. But suppose you're now told to create your own cake. If you don't know what ingredients are important to the rising process or the flavor or the texture and so on, then you're limited only to the one cake you know how to bake and you can never grow. Understanding the chemical responses is more difficult than memorizing the recipes, but if you're to be successful at baking, you need to know at least the basics. Similarly, if you're to be successful at math, you need to have a fundamental understanding of why things work the way they do.
(I only skimmed a bit of the quoted article (and intend to read it all later), but it's encouraging to know that I'm not alone in this line of thinking. After hearing stuff this year from others who've been in the biz longer than I, I was beginning to think perhaps I was a foolish young optimist. At least now I know there are a handful of foolish older optimists as well ^__^)
Meanwhile, there are also those students that say, "But I got A's in high school -- how can I be failing now?" According to a study done in 2008 by the Strong American Schools, "nearly four out of five remedial students had a high school GPA of 3.0 or higher." (CNSNews.com) When schools with better results get more state funding, it's only natural that grades are going to be inflated. Unfortunately, what results is an overall poor assessment of student learning, which is now leading to poor preparedness for college. However, new data suggests that the problem of grade-inflation may not necessarily originate in high school.
One of the larger puzzles in NY education over the past few years is determining why students in elementary school score well on state exams in English and math, but then by the time students reach middle school or high school, scores drop considerably. Apparently, the Utica OD reports, that there's been some "tougher grading" on state exams in 2010 than in 2009, which has lead to fewer students passing. In other words, the state has changed the guidelines regarding how state exams are to be graded to be more rigorous in 2010. And the difference in scores is staggering.
For example, the average percent of students in Oneida County that passed the state math exam in 2009 was 90.3%. Compare that to a passing rate of 61.3% in 2010. Additionally, of the 14 schools that reported a passing success rate of 100% in 2009, half of them reported a passing success rate of 60% or less in 2010.
Although the difference is incredible, I think the "tougher" grading may just be a more accurate assessment. Now, I don't know much about the exams or how they were changed or how the grading was made "tougher" but if the average passing rate of 3rd-to-8th-graders is actually 61.3%, that means that 38.7% of students that age are or should be in remedial classes. The 40% of college students enrolled in remedial courses, then, is not so much a surprise if students as far back as 3rd grade are not being accurately assessed.
Because I've always been interested in this sort of stuff, I constructed some tables using the data from the OD (which you can find here). I looked at only Oneida County schools (because of the way the data's reported, I had to retype it all in Excel to be able to work with it, so I figured I'd limit myself to just one county) and the students being assessed are in grades 3 through 8. I also combined some of the info with data from the New York Schools website.
And now, witness the result of a morning of number crunching & HTML tables!
Average percent of Oneida County students that passed
the state math
exam in 2009 and 2010 (by grade level)
3rd Grade
4th Grade
5th Grade
6th Grade
7th Grade
8th Grade
2009
94.0
87.8
91.0
87.0
93.5
86.8
2010
58.3
63.5
61.5
60.9
65.4
59.1
Average Percent of Students in Grades 3-8 Who Passed
the State Math Exam
in Oneida County (by school district)
School District
Total Number of
Students *
2009
2010
Adirondack Central
1,460
91.4%
51.7%
Camden Central
2,741
91.3%
66.3%
Clinton Central
1,511
91.9%
66.5%
Holland Patent Central
1,775
89.5%
57.3%
New Hartford Central
2,656
95.6%
74.4%
New York Mills Union Free
602
90.6%
70.7%
Oriskany Central
739
94.9%
58.8%
Remsen Central
567
88.8%
53.9%
Rome City
5,817
87.2%
51.2%
Sauquoit Valley Central
1,237
95.6%
71.6%
Utica City
9,041
82.2%
49.4%
Vernon-Verona-Sherrill City
2,372
94.5%
70.9%
Waterville Central
936
92.6%
63.1%
Westmoreland Central
1,106
90.4%
60.2%
Whitesboro Central
3,671
94.4%
74.3%
* This info comes
from the
New York Schools website.
Oneida County Schools with Biggest Difference
in % of Students
Passing from 2009 to 2010
Difference
School
District
Grade
-70.6
Forestport Elementary
Adirondack Central
3
-58.2
Stokes Elementary
Rome City
3
-56.9
Bellamy Elementary
Rome City
4
-56.1
North Bay Area
Camden Central
3
-53.7
Remsen
Remsen Central
3
-52.6
Martin Luther King Jr Elementary
Utica City
4
-52.3
Oriskany
Oriskany Central
3
-52.3
Sauquoit Valley
Sauquoit Valley Central
3
-52.2
Oriskany
Oriskany Central
8
-50.9
John E Joy Elementary
Rome City
3
Oneida County Schools with Smallest Difference
in % of Students
Passing from 2009 to 2010
Difference
School
District
Grade
-1.3
E A Mcallister Elementary
Vernon-Verona-Sherrill City
6
+2.1
Harts Hill School
Whitesboro Central
4
+2.9
North Bay Area
Camden Central
4
-4.9
E A Mcallister Elementary
Vernon-Verona-Sherrill City
4
-5.3
New York Mills
New York Mills Union Free
6
-6.7
New York Mills
New York Mills Union Free
4
-7.2
Thomas Jefferson Elementary
Utica City
5
-7.5
Sauquoit Valley
Sauquoit Valley Central
8
-7.9
Sauquoit Valley
Sauquoit Valley Central
4
-8.9
Hughes Elementary School
New Hartford Central
3
And, for the halibut, here's a scatter plot of district passing rates, to see if the 2009% passing rate and the 2010% passing rate were at all correlated. It would seem not very (r = 0.521)...

(click for full size image)
I find all this stuff fascinating anyway, but it's particularly appropriate since I'll be teaching remedial math this year. These are the courses I'm most concerned about because of the way they're taught, although I've also heard a rumor that they're thinking of changing that. Right now, my understanding is that things are fairly similar to the rigid old-school method described here (just under the "too many rules" subheading). It's definitely going to be an interesting semester, that's for sure.
On a related note, I guess you can tell what you're truly passionate about when you keep researching & writing through breakfast and lunch, and suddenly you discover it's 3:15pm when just a moment ago it was only a few minutes 'til 9:00am.
...I'm'a go find some food, I think...