Math HW full score! <3
I got full score on my latest math HW! We had a rather interesting proof on there about the direct sums of a series of subspaces being isomorphic to a function that returns an ordered tuple with a value at only ONE of the coordinates.
^___^ I feel proud! Our grader put "good!" on it!
A very interesting proof we did recently was this:
golem.ph.utexas.edu/category/2010/09/bimonoids_from_biproducts.html#more
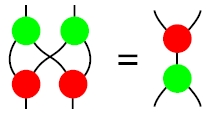
Here, the green circle represents a diagonal map - in other words, we take a vector (v) and we send it off in two directions, changing it to (v,v). The red circle represents a codiagonal map which takes two vectors, say (v,w) and changes them to v+w.
So you can see that the two inputs on the LEFT can be represented as v and w. We are saying we are going to first put these two inputs through the diagonal map, changing it from (v,w) --> (v,v,w,w).
Then we shall switch them up as the lines indicate, a v and a w to each side. That's represented by (v,v,w,w) --> (v,w,v,w). We then run them through the codiagonal, which adds elements. (v,w,v,w,)--> (v+w,v+w)
So in all, the transformations run like this: (v,w,) --> (v,v,w,w) --> (v,w,v,w) --> (v+w,v+w)
---------------------
Now we'll prove that this result is the same as the diagram on the RIGHT. So here, we have two inputs, v and w, which are fed into the red blob. (v,w)-->(v+w)
It goes to the green blob, which sends them off in two directions. (v+w) --> (v+w,v+w)
Obviously, we've reached the same conclusion as the left.
-------------------
Now, the question is, how is this used in real life? I have no idea. ^__^ But it's a rather interesting and almost contradictory result.
^___^ I feel proud! Our grader put "good!" on it!
A very interesting proof we did recently was this:
golem.ph.utexas.edu/category/2010/09/bimonoids_from_biproducts.html#more

Here, the green circle represents a diagonal map - in other words, we take a vector (v) and we send it off in two directions, changing it to (v,v). The red circle represents a codiagonal map which takes two vectors, say (v,w) and changes them to v+w.
So you can see that the two inputs on the LEFT can be represented as v and w. We are saying we are going to first put these two inputs through the diagonal map, changing it from (v,w) --> (v,v,w,w).
Then we shall switch them up as the lines indicate, a v and a w to each side. That's represented by (v,v,w,w) --> (v,w,v,w). We then run them through the codiagonal, which adds elements. (v,w,v,w,)--> (v+w,v+w)
So in all, the transformations run like this: (v,w,) --> (v,v,w,w) --> (v,w,v,w) --> (v+w,v+w)
---------------------
Now we'll prove that this result is the same as the diagram on the RIGHT. So here, we have two inputs, v and w, which are fed into the red blob. (v,w)-->(v+w)
It goes to the green blob, which sends them off in two directions. (v+w) --> (v+w,v+w)
Obviously, we've reached the same conclusion as the left.
-------------------
Now, the question is, how is this used in real life? I have no idea. ^__^ But it's a rather interesting and almost contradictory result.