Неконструктивное доказательство.
Играясь с иррациональными числами, можно задаться вопросом: а существуют ли два иррациональных числа 
и
, таких, что число
, то есть является рациональным?
Все те же лица, плюс птички:

Ответ на поставленный вопрос положительный, причем этому факту есть простое и изящное доказательство.
Теорема.
Существуют такие иррациональные
и
, что
.
Доказательство.
Мы знаем, что число
- иррационально. Положим
Возможны два варианта: либо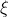
рационально, и тогда теорема доказано, либо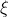
иррационально. Но тогда
^{\sqrt{2}}=\sqrt{2}^{2}&space;=2\in\mathbb{Q}.)
Теорема доказана.
Забавно, что доказательство не позволяет дать ответ на вопрос какие две пары иррациональных чисел удовлетворяют условию теоремы. Сейчас уже известно, что
- иррационально, то есть искомая пара это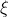
и
. Однако, доказать иррациональность
оказывается очень непросто. Этот факт следует из теоремы Гельфонда-Шнайдера, доказанной в 1934 (sic!) году советским математиком Александром Гельфондом и, независимо, в 1935 году немецким математиком Теодором Шнайдером,
А вообще, теорема Гельфонда-Шнайдера является решением 7-й проблемы Гильберта, на минуточку.
Остается лишь отметить, что опираясь на существование трансцендентных чисел, можно достаточно легко строить в явном виде иррациональные числа
и
, такие, что
. Однако, это уже совсем другая история.
UPD. В качестве упражнения, попробуйте доказать иррациональность числа
. Тогда
^{2\log_23}=3\in\mathbb{Q}.)
и
, таких, что число
, то есть является рациональным?
Все те же лица, плюс птички:

Ответ на поставленный вопрос положительный, причем этому факту есть простое и изящное доказательство.
Теорема.
Существуют такие иррациональные
и
, что
.
Доказательство.
Мы знаем, что число
- иррационально. Положим
Возможны два варианта: либо
рационально, и тогда теорема доказано, либо
иррационально. Но тогда
Теорема доказана.
Забавно, что доказательство не позволяет дать ответ на вопрос какие две пары иррациональных чисел удовлетворяют условию теоремы. Сейчас уже известно, что
- иррационально, то есть искомая пара это
и
. Однако, доказать иррациональность
оказывается очень непросто. Этот факт следует из теоремы Гельфонда-Шнайдера, доказанной в 1934 (sic!) году советским математиком Александром Гельфондом и, независимо, в 1935 году немецким математиком Теодором Шнайдером,
А вообще, теорема Гельфонда-Шнайдера является решением 7-й проблемы Гильберта, на минуточку.
Остается лишь отметить, что опираясь на существование трансцендентных чисел, можно достаточно легко строить в явном виде иррациональные числа
и
, такие, что
. Однако, это уже совсем другая история.
UPD. В качестве упражнения, попробуйте доказать иррациональность числа
. Тогда