Международная система единиц для попаданца. Часть 1.
Книг, в которых главный герой проваливается в прошлое либо попадает в параллельные и не очень миры, в своем теле или переносом сознания, нынче написано превеликое множество. Изрядная часть попаданцев, из тех, коим повезло загреметь в менее технически развитый социум, начинают испытывать тягу к прогрессорству. Дальнейшая скорость движения осчастливленных дикарей в светлое индустриальное общество ограничивается лишь здравым смыслом автора.
Вместе с тем, при провале в достаточно отдаленное прошлое, в особенности при перемещении сознания, первым шагом на пути технического прогресса должно стать построение основных эталонных единиц СИ: метра, секунды, килограмма, а, в перспективе, и ампера. Первым и, пожалуй, единственным, попавшимся мне в руки художественным произведением, автор которого полностью осознал важность указанной задачи стал "Кембрийский период" Владимира Коваленко (aka k_und_k). Респект и уважуха, да.

Главный герой оказывается перемещен в прошлое и поселен в теле местного фольклорного персонажа, сиды (на иллюстрации справа, как я понимаю). В настоящий момент история насчитывает уже три тома, причем последний был написан и выложен в открытый доступ автором на средства, добровольно пожертвованные читателями. Один из первых, насколько мне известно, подобных случаев в русскоговорящем интернете.
К сожалению, решение задачи, найденное автором, оставляет желать лучшего: главная героиня, Немайн, измеряла высоту речного обрыва, сбрасывая камни в воду и подсчитывая количество ударов пульса за время падения (ровно 5, если кому интересно). Моя нижняя оценка относительной погрешности такого метода дает 10%, что, пожалуй, многовато.
Для решения сформулированной в пятницу "Задачке о попаданце" было предложено изрядное количество различных подходов, эксплуатирующих самые разные физические явления (и не только). К сожалению, далеко не все решения удовлетворяют драконовскому условию 1% относительной погрешности.
В первой части я опишу подход, который представляется мне наиболее предпочтительным и точным. Во второй части (завтра/послезавтра) - разберем иные предложенные варианты.
Начнем с метра и секунды.
Одновременно построить эталон длины и времени нам позволит применение математического маятника. Так как по условию, наш герой остается на Земле, то ускорение свободного падения нам известно.
Период математического маятника описывается формулой:

Здесь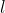
- длина подвеса, а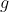
- ускорение свободного падения.
Отсюда
^2)
В свою очередь, период колебаний маятника модно найти, посчитав число колебаний за определенный, заранее известный период времени:

Окончательно:
^2.)
В качестве этолонного промежутка времени, очевидно, нужно использовать сутки. Да, невозможно не согласиться, что путь этот крайне трудозатратный, однако использование различных геометрических построений, сокращающих необходимое время наблюдения, одновременно значительно увеличивают погрешность.
Критически настроенный читатель может в этом месте заявить: ну и откуда следует, что предлагаемый метод удовлетворяет условию на погрешность?
Продемонстрируем это.
Методом логарифмирования, получим что верхняя оценка относительной погрешности формулы определения длины равна:

Ускорение свободного падения зависит от географических координат точки, однако мы можем заведомо считать
Соответственно,

При выборе подходящей яркой звезды, наблюдая ее заход за достаточно удаленный объект с четкой границей (например, за гору, Стоунхендж тоже подойдет), можно добиться достаточно точной отсечки границы звездных суток, с абсолютной погрешностью менее 30 секунд, что дает нам относительную погрешность

В итоге и получим, что верхняя оценка относительной погрешности
Реальная погрешность будет, разумеется, меньше.
Можно ли улучшить этот результат? Разумеется!
Во-первых, мы можем проводить наблюдения не одни, а несколько суток подряд, считая, считая, считая колебания маятника. Трудоемкость измерений существенно возрастет, но и точность вырастет значительно. Однако, временная компонента и так определяется очень точно.
Во-вторых, определив, пусть и грубо, географическую широту места наблюдения, можно воспользоваться широтной эмпирической формулой:

Точность ее столь высока, что в нашем случае мы можем считать ее погрешность пренебрежимо малой. Другое дело, что воспользоваться ею, без микрокалькулятора в руках, в условиях античности - не так-то и просто. Хотя, разумеется, и вполне возможно.
Остается определить килограмм. Большинство читателей в этот момент предложило опереться на известную плотность воды 1 г/см3, сконструировав прямоугольный сосуд. Не отрицая реализуемость подобного решения, считаю, что изящный трюк, предложенный автором "Кембрийского периода", более технологичен. Он предлагает вырезать из плавучего материала (дерева, разумеется), прямоугольный параллелепипед и затем поместить его в воду. Отмерив, насколько глубоко погрузился брусок, мы можем найти объем вытесненной им воды, вес которой, по закону Архимеда, будет равен весу бруска. Вот вам и готовый эталон массы. А какой формы бочка, в которой брусок купать - вовсе безразлично.
Совсем въедливый читатель заметит здесь, что тем же самым логарифмическим методом мы получим относительную погрешность килограмма, как производной от метра величины:

Что дает нам 1.1% - больше, чем требуется условием. Так что, придется, придется нашему естествоиспытателю улучшать точность построения эталона длины до погрешности 0.33%. Горек хлеб античного метролога.
Продолжение.
Вместе с тем, при провале в достаточно отдаленное прошлое, в особенности при перемещении сознания, первым шагом на пути технического прогресса должно стать построение основных эталонных единиц СИ: метра, секунды, килограмма, а, в перспективе, и ампера. Первым и, пожалуй, единственным, попавшимся мне в руки художественным произведением, автор которого полностью осознал важность указанной задачи стал "Кембрийский период" Владимира Коваленко (aka k_und_k). Респект и уважуха, да.

Главный герой оказывается перемещен в прошлое и поселен в теле местного фольклорного персонажа, сиды (на иллюстрации справа, как я понимаю). В настоящий момент история насчитывает уже три тома, причем последний был написан и выложен в открытый доступ автором на средства, добровольно пожертвованные читателями. Один из первых, насколько мне известно, подобных случаев в русскоговорящем интернете.
К сожалению, решение задачи, найденное автором, оставляет желать лучшего: главная героиня, Немайн, измеряла высоту речного обрыва, сбрасывая камни в воду и подсчитывая количество ударов пульса за время падения (ровно 5, если кому интересно). Моя нижняя оценка относительной погрешности такого метода дает 10%, что, пожалуй, многовато.
Для решения сформулированной в пятницу "Задачке о попаданце" было предложено изрядное количество различных подходов, эксплуатирующих самые разные физические явления (и не только). К сожалению, далеко не все решения удовлетворяют драконовскому условию 1% относительной погрешности.
В первой части я опишу подход, который представляется мне наиболее предпочтительным и точным. Во второй части (завтра/послезавтра) - разберем иные предложенные варианты.
Начнем с метра и секунды.
Одновременно построить эталон длины и времени нам позволит применение математического маятника. Так как по условию, наш герой остается на Земле, то ускорение свободного падения нам известно.
Период математического маятника описывается формулой:
Здесь
- длина подвеса, а
- ускорение свободного падения.
Отсюда
В свою очередь, период колебаний маятника модно найти, посчитав число колебаний за определенный, заранее известный период времени:
Окончательно:
В качестве этолонного промежутка времени, очевидно, нужно использовать сутки. Да, невозможно не согласиться, что путь этот крайне трудозатратный, однако использование различных геометрических построений, сокращающих необходимое время наблюдения, одновременно значительно увеличивают погрешность.
Критически настроенный читатель может в этом месте заявить: ну и откуда следует, что предлагаемый метод удовлетворяет условию на погрешность?
Продемонстрируем это.
Методом логарифмирования, получим что верхняя оценка относительной погрешности формулы определения длины равна:
Ускорение свободного падения зависит от географических координат точки, однако мы можем заведомо считать
Соответственно,
При выборе подходящей яркой звезды, наблюдая ее заход за достаточно удаленный объект с четкой границей (например, за гору, Стоунхендж тоже подойдет), можно добиться достаточно точной отсечки границы звездных суток, с абсолютной погрешностью менее 30 секунд, что дает нам относительную погрешность
В итоге и получим, что верхняя оценка относительной погрешности
Реальная погрешность будет, разумеется, меньше.
Можно ли улучшить этот результат? Разумеется!
Во-первых, мы можем проводить наблюдения не одни, а несколько суток подряд, считая, считая, считая колебания маятника. Трудоемкость измерений существенно возрастет, но и точность вырастет значительно. Однако, временная компонента и так определяется очень точно.
Во-вторых, определив, пусть и грубо, географическую широту места наблюдения, можно воспользоваться широтной эмпирической формулой:

Точность ее столь высока, что в нашем случае мы можем считать ее погрешность пренебрежимо малой. Другое дело, что воспользоваться ею, без микрокалькулятора в руках, в условиях античности - не так-то и просто. Хотя, разумеется, и вполне возможно.
Остается определить килограмм. Большинство читателей в этот момент предложило опереться на известную плотность воды 1 г/см3, сконструировав прямоугольный сосуд. Не отрицая реализуемость подобного решения, считаю, что изящный трюк, предложенный автором "Кембрийского периода", более технологичен. Он предлагает вырезать из плавучего материала (дерева, разумеется), прямоугольный параллелепипед и затем поместить его в воду. Отмерив, насколько глубоко погрузился брусок, мы можем найти объем вытесненной им воды, вес которой, по закону Архимеда, будет равен весу бруска. Вот вам и готовый эталон массы. А какой формы бочка, в которой брусок купать - вовсе безразлично.
Совсем въедливый читатель заметит здесь, что тем же самым логарифмическим методом мы получим относительную погрешность килограмма, как производной от метра величины:
Что дает нам 1.1% - больше, чем требуется условием. Так что, придется, придется нашему естествоиспытателю улучшать точность построения эталона длины до погрешности 0.33%. Горек хлеб античного метролога.
Продолжение.