bootstrap и квантили
Есть подозрение, что в bootstrap-семплировании для некоторых статистик можно избежать собственно семлирования, честно по формуле посчитав мат-ожидание результата или [2.5%, 97.5%] интервал распределения результата.
Выборка с возвращением в bootstrap - это тоже самое что и семплирование из эмпирического распределения выборки
обозначим эту эмпирическую функцию распределения как F̂
применим F̂-1 к равномерно распределённой на [0, 1] величине U(0,1), получим снова распределение F̂
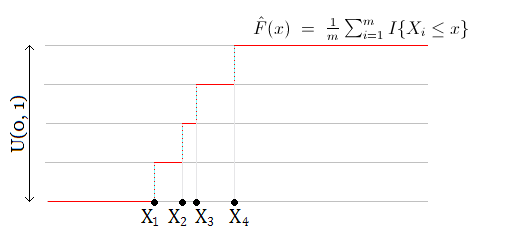
Чтобы создать одну bootstrap-выборку - можно взять выборку из n штук из U(0, 1) чисел и применить к ним F̂-1
медиана bootstrap-выборки - это применение F̂-1 к i-й порядковой статистике, где i равно n/2.
i-я порядковая статистика U(0, 1) - это вдоль и поперёк изученное бета-распределение
Берем это бета-распределение, берем его [2.5%, 97.5%] интервал распределения (через неполную бета-функцию или приближение нормальным распределением), втыкаем его границы в F̂-1, получаем интервал в котором (97.5% - 2.5%) будет bootstrap-медиана
Таким же образом можно получать остальные квантили, не только медиану.
Велосипед? Или грабли? Или это настолько очевидно, что так всегда и делается?
Выборка с возвращением в bootstrap - это тоже самое что и семплирование из эмпирического распределения выборки
обозначим эту эмпирическую функцию распределения как F̂
применим F̂-1 к равномерно распределённой на [0, 1] величине U(0,1), получим снова распределение F̂
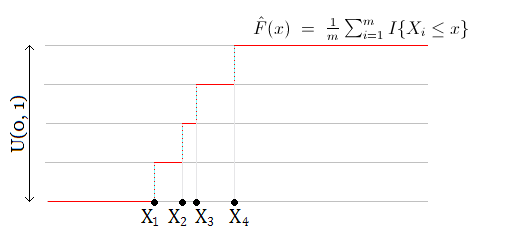
Чтобы создать одну bootstrap-выборку - можно взять выборку из n штук из U(0, 1) чисел и применить к ним F̂-1
медиана bootstrap-выборки - это применение F̂-1 к i-й порядковой статистике, где i равно n/2.
i-я порядковая статистика U(0, 1) - это вдоль и поперёк изученное бета-распределение
Берем это бета-распределение, берем его [2.5%, 97.5%] интервал распределения (через неполную бета-функцию или приближение нормальным распределением), втыкаем его границы в F̂-1, получаем интервал в котором (97.5% - 2.5%) будет bootstrap-медиана
Таким же образом можно получать остальные квантили, не только медиану.
Велосипед? Или грабли? Или это настолько очевидно, что так всегда и делается?