bayes theorem illustration
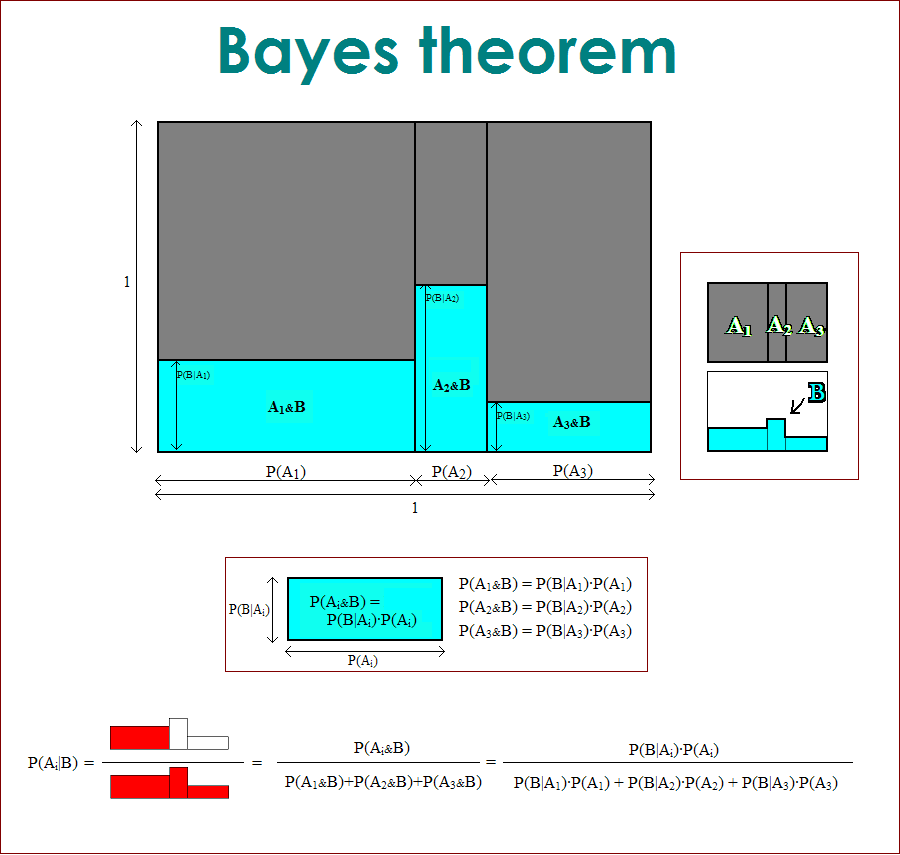
Когда в универе впервые рассказали про теорему байеса, было непонятно что это такое. Ну взяли определение
P(A|B) = P(A&B)/P(B),
разделили на такое же симметричное равенство
P(B|A) = P(A&B)/P(A),
P(A&B) сократилось, получили теорему байеса
P(A|B) = P(B|A)·P(A)/P(B)
Совершенно тривиальное доказательство на уровне подстановки букв. Одновременно с этим - непонятно, как привязано к реальности. Постоянно путаешь, что там в знаменателе, что в числителе, что надо ставить справа от |, а что слева. Почему B или A - это априорные или апостериорные вероятности, ведь B от A в доказательстве ничем не отличаются (P(болезнь|видимый симптом) - апостериорная, P(болезнь вообще) - априорная).
У нас препод был формалист, он даже не объяснил почему условная вероятность называется условной. Вот вам детки определения, вот аксиомы. Борелевскаясигмаалгебра - это минимальнаясигмаалгебрасодержащаявсеоткрытыеподмножества, переходим к интегралу лебега. Подстанавливаем буквы в формулы, получаем новые формулы.
Тогда нарисовал себе картинку, что бы легче было применять её для решения задач типа:
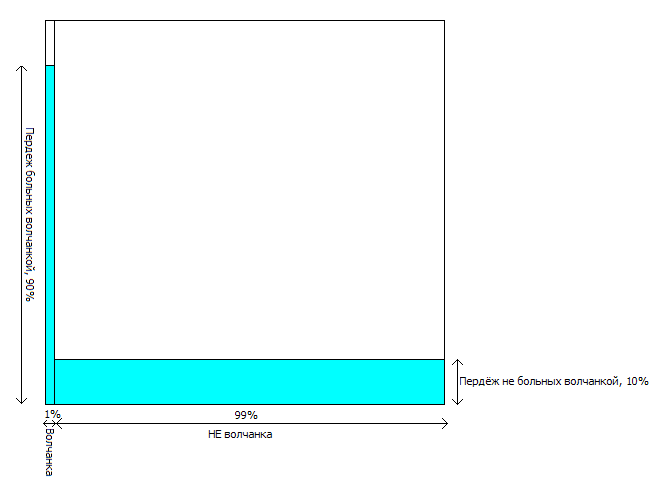
Если пациента у волчанка, то он пердит с вероятностью 90%, если болеет не волчанкой - то пердит с вероятностью 10%, всего волчанкой болеют 1% пациентов. Пациент пернул, надо выяснить насколько велика вероятность волчанки.
И визуальное решение задачи про волчанку. Видно, что, несмотря на кажущуюся надёжность симптома пердежа, среди больных с этим с симптомом доля больных волчанкой (вертикальный синий прямоугольник справа) заметно меньше, чем доля не больных (синий прямоугольник снизу справа):
P(A|B) = P(A&B)/P(B),
разделили на такое же симметричное равенство
P(B|A) = P(A&B)/P(A),
P(A&B) сократилось, получили теорему байеса
P(A|B) = P(B|A)·P(A)/P(B)
Совершенно тривиальное доказательство на уровне подстановки букв. Одновременно с этим - непонятно, как привязано к реальности. Постоянно путаешь, что там в знаменателе, что в числителе, что надо ставить справа от |, а что слева. Почему B или A - это априорные или апостериорные вероятности, ведь B от A в доказательстве ничем не отличаются (P(болезнь|видимый симптом) - апостериорная, P(болезнь вообще) - априорная).
У нас препод был формалист, он даже не объяснил почему условная вероятность называется условной. Вот вам детки определения, вот аксиомы. Борелевскаясигмаалгебра - это минимальнаясигмаалгебрасодержащаявсеоткрытыеподмножества, переходим к интегралу лебега. Подстанавливаем буквы в формулы, получаем новые формулы.
Тогда нарисовал себе картинку, что бы легче было применять её для решения задач типа:
Если пациента у волчанка, то он пердит с вероятностью 90%, если болеет не волчанкой - то пердит с вероятностью 10%, всего волчанкой болеют 1% пациентов. Пациент пернул, надо выяснить насколько велика вероятность волчанки.

И визуальное решение задачи про волчанку. Видно, что, несмотря на кажущуюся надёжность симптома пердежа, среди больных с этим с симптомом доля больных волчанкой (вертикальный синий прямоугольник справа) заметно меньше, чем доля не больных (синий прямоугольник снизу справа):
