Историческая динамика. Взгляд с позиций синергетики (часть 1)
(источник)
Историческая динамика. Взгляд с позиций синергетики
( Historical Dynamics. Synergetics Approach
Preprint, Inst. Appl. Math., the Russian Academy of Science)
Курдюмов С.П., Малинецкий Г.Г., Подлазов А.В.
(S.P.Kurdyumov, G.G.Malinetski, A.V.Podlazov)
ИПМ им. М.В.Келдыша РАН
Москва, 2004
Аннотация
В 1994 году была выдвинута исследовательская программа, связанная с построением теоретической истории. В основе этой программы лежало исследование возможных траекторий исторического развития с помощью компьютерного моделирования, широкого использования методов естественных и гуманитарных наук. Этот подход может сыграть исключительно важную роль с точки зрения стратегического планирования как на национальном, так и на глобального уровне. В последующие годы удалось существенно продвинуться в реализации междисциплинарного проекта, связанного с теоретической историей. Работа посвящена обсуждению нескольких принципиальных результатов, полученных в ходе этих исследований.
Abstract
The research program of theoretical history creation was put forward in 1994. This program was based on the investigation of possible historical development trajectories on basis by means of computer simulation, broad use of methods of natural and humanitarian sciences. This approach can be vary important from the point of view of the strategic planning on both national and global levels. During the ensuing years we succeeded in the realization of interdisciplinary project of theoretical history. Here we consider several fundamental results of these researches.
Со времен Ф. Броделя ведущим процессом в исторической науке стала дифференциация и специализация. Развивались экономическая история, историческая демография, историческая культурология, историческая география и т.д. Как и предсказывал французский исследователь, родились историческая психология и историческая социология. Сейчас настоятельно ощущается потребность в междисциплинарном синтезе, в подходах, позволяющих из множества аспектов, изучаемых различными науками, выделить главное, найти ключевые причинно-следственные связи и наиболее важные переменные.
В качестве основы для такого подхода наиболее естественно использовать теорию самоорганизации, или синергетику. Поэтому большой интерес представляют проекты, направленные на развитие своеобразного синергетического подхода в истории. Здесь возникает новый взгляд на традиционные исторические проблемы, связанный с реконструкцией прошедшего, с попыткой увидеть неожиданные, парадоксальные связи в событиях прошлого. И напротив, в событиях прошлого, кажущихся случайными и трудно объяснимыми, удается проследить универсальные системные механизмы. С другой стороны, создаваемые модели исторических процессов могут оказаться принципиально важными для анализа мировой динамики и для стратегического планирования.
При этом прошлое выступает как своеобразный полигон, обеспечивающий верификацию создаваемых концепций и математических описаний. Это позволяет взглянуть на историю не только как на ретроспективную науку, подобную астрономии или эволюционной биологии, где эксперимент невозможен и можно лишь восходить от следствий к причинам, но и как на перспективную, где существует и обратный ход - от выявленных при анализе исторического материала взаимосвязей, типичных сценариев событий к задачам прогноза.
ПАРАМЕТРЫ ПОРЯДКА В ИСТОРИЧЕСКИХ ПРОЦЕССАХ
Для использования представлений и методов синергетики принципиально наличие параметров порядка (одной или нескольких ведущих переменных, определяющих динамику всех остальных процессов). [1,2] Таим параметром при анализе многих исторических процессов является численность населения.
Математическое моделирование демографических процессов восходит еще к XVIII веку. Английский монах Мальтус сформулировал популяционный принцип. В соответствии с ним рост человечества описывается геометрической прогрессией, в то же время производство пищи растет по арифметической прогрессии. Исходя из этого принципа, Мальтус делал вывод о неизбежности войн, в которых будет истребляться значительная часть человечества.
Исследования профессора С.П. Капицы [3] показали, что Мальтус был неправ. В течение всей истории человечества его численность росла быстрее, чем по геометрической прогрессии, как утверждал Мальтус.
Она росла по гиперболическому закону
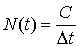
, (1)
где Dt = t‑2025, N - численность человечества, а C - постоянная, равная приблизительно 200 млрд. чел.×год. Это очень быстрый рост. К примеру, в 1700 году жителей на Земле было в 10 раз меньше, чем теперь. В начале царствования Петра I в России было всего 10 миллионов человек.
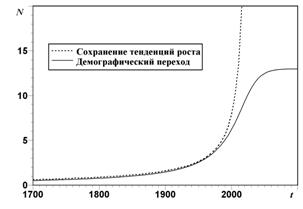
Рис. 1. Рост народонаселения мира
Графики, представляющие два различных сценария будущего развития, стремительно расходятся.
При сохранении тенденций, действовавших в течении всей предшествующей истории, численность человечества стала бы бесконечной приблизительно к 2025 г.
При демографическом переходе происходит замедление роста с вероятной стабилизаций народонаселения.
В настоящее время население мира растет на более чем на 1% в год при среднегодовом приросте свыше 70 миллионов человек.
Быстрый рост населения прежде всего в развивающихся странах в 50‑60‑е годы, во многом связанный с увеличением продолжительности жизни, обусловленной повышением качества медицинского обслуживания, получил название демографического взрыва.
В эти годы многие ученые считали, что ограничение численности населения в будущем будет связано с нехваткой продовольствия, поскольку и в настоящее время по данным ООН более 1 миллиарда человек голодает.
Однако ситуация оказалась совсем иной. Ученые, анализируя рост населения разных стран и мира в целом, столкнулись с важным и интересным явлением - демографическим переходом. Этот переход - постепенное изменение закона роста численности населения, замедление этого роста и последующая стабилизация численности (см. рис. 1 и рис. 2).
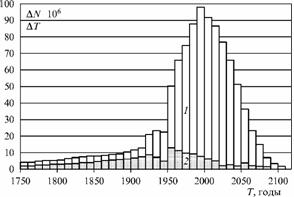
Рис. 2. Демографический переход
Прирост населения мира с 1750 по 2100 гг., усредненный за декады.
1 - развивающиеся страны, 2 - развитые.
Причем демографический переход происходит не в слаборазвитых странах, для которых характерны нехватка продовольствия и энергии, а в странах благополучных. Впервые демографический переход наблюдали в прошлом веке во Франции и Швеции. В настоящее время он произошел в большинстве европейских стран. В некоторых из них, например в Норвегии и Германии, рождаемость оказалась в последние десятилетия настолько низкой, что правительства этих стран начали активно привлекать иммигрантов для работы в ряде секторов экономики. Естественно, демографический переход кардинально меняет возрастную структуру общества (см. рис. 3). Продолжительность жизни возрастает, а население стареет, что непосредственно отражается на экономике и социальной структуре общества.
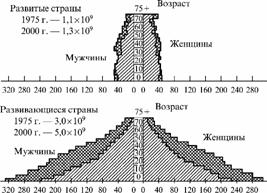
Рис. 3. Распределение населения мира по возрасту и полу в 1975 и 2000 г.г.
При демографическом переходе меняется возрастная структура.
Общество стареет, у него появляются новые проблемы.
Ожидающие нас в XXI веке изменения радикальны. Страна или город, в которых из десятилетия в десятилетие живет одно и то же число людей, должна иметь совсем другие технологии, другую мораль, другие культурные нормы. Банальнейший аналог здесь - средневековье, когда деревням было не под силу прокормить слишком большие города.
С позиций этой теории и теории режимов с обострением (пример величины, растущей в режиме с обострением дает закон (1)) [4], была проанализирована география расселения и выявлены условия, при которых возможно качественное изменение системы расселения - переход "экспансия-сосредоточение" [5,6]. Для миграции населения был введен некоторый феноменологический нелинейный закон. Проведенный анализ модели показал, что стадия экспансии, происходящей с уменьшением плотности населения, может быть характерна не для ослабленных этносов, как можно было бы предположить, а для обществ, имеющих большой потенциал развития. И затем случайные субъективные факторы могут прервать этот процесс, резко увеличив концентрацию населения в одном или нескольких городах или регионах.
ДЕМОГРАФИЧЕСКИЙ ПЕРЕХОД И ЖИЗНЕСБЕРЕГАЮЩИЕ ТЕХНОЛОГИИ
Нелинейность, присущая закону роста числа людей на планете, в соответствии с концепцией С.П. Капицы, обусловлена "информационным взаимодействием", действовавшим и миллион лет назад, и ныне. Эта теория имеет ряд внутренних трудностей и не объясняет непротиворечивым образом демографический переход, происходящий в последние десятилетия. Кроме того эта теория не позволяет выявить другие параметры порядка и предсказать траекторию мирового сообщества в случае их изменения.
В последние годы была развита альтернативная теория, связывающая нелинейность демографических процессов с развитием жизнесберегающих технологий (т.е. технологий, помогающих спасать людей и увеличивать продолжительность их жизни). С этих позиций, демографический переход связан с "насыщением" имеющихся технологий. На этой основе удается выявить системные механизмы гражданских войн, объяснить неоднократно наблюдавшийся в истории эффект "насыщения имперских технологий" (поздний Рим, крушение ряда других империй) и предсказать "полосу нестабильности", в которую вступает человечество в начавшемся веке. [7,8] Обсудим этот результат более подробно.
Формулу (1) можно переписать в виде дифференциального уравнения

. (2)
Его вид говорит о самоускоряющемся росте N или, что тоже самое, о сокращение масштаба времени, на котором происходят существенные демографические изменения, т.е. об ускорении хода истории.
Ключевым для описания процесса роста народонаселения является понятие жизнесберегающих технологий, под которыми понимаются любые знания, навыки или традиции, которые могут быть использованы для спасения человека от смерти или продления его жизни. Уровень развития жизнесберегающих технологий p будем характеризовать уменьшением среднего коэффициента смертности kd, достигнутым благодаря их действию, т.е. p = Dkd = kd ‑ kd0, гдеkd0 » 0,06 год‑1 коэффициент смертности первобытного человека. [7,8]
В предположении постоянства среднего коэффициента рождаемости для скорости роста народонаселения получаем уравнение
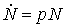
. (3)
Жизнесберегающие технологии не требуют для своего создания какого-то специального механизма. Являясь основой существования человечества, сутью человеческой культуры, они создаются людьми в процессе повседневной жизнедеятельности, т.е. на основе уже имеющихся жизнесберегающих технологий. Соответственно, для скорости их появления можно записать уравнение
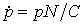
, (4)
константа C в котором определяет трудозатраты, необходимые на увеличение p в e раз при постоянном N.
Интегрируя систему (3)-(4), получаем основное уравнение теоретической демографии
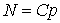
. (5)
Оно означает, что уровень развития жизнесберегающих технологий p, описывающий скорость роста народонаселения, характеризует в то же время размер экологической ниши человечества.
Может так случиться, что предписанный уравнением (5) баланс между уровнем жизнесберегающих технологий и населением по каким-то причинам где-то локально нарушается. Если в результате войн, эпидемий, стихийных бедствий и т.п. катаклизмов население уменьшается, то status quoвосстанавливается в течение всего лишь нескольких поколений. Если же, напротив, по каким-то причинам произошло чрезмерное увеличение численности населения, не сопровождаемое одновременным развитием технологий, то для появляющихся людей может просто не найтись места в социальной структуре общества, которая адекватна достигнутому уровню развития жизнесберегающих технологий. Возникающий при этом избыток людской численности обычно снимается посредством войн, которые в своем большинстве имеют демографическую, а не экономическую природу. [7,8]
Подстановка решения (5) в уравнение (3) немедленно приводит к уравнению (2), полученному ранее путем анализа демографических данных.

Рис. 4. Развитие технологий в последние века
В отличии от общего технологического уровня, уровень жизнесберегающих технологий выходит на насыщение.
Развитие жизнесберегающих имеет естественный предел, обусловленный тем, что нельзя спасти от смерти больше людей, чем их всего живет. Т.е. уровень жизнесберегающих технологий должен выйти на насыщение, в то время как рост общего технологического уровня будет продолжаться, как показано на рис. 4. Прекращение развития жизнесберегающих технологий означает, что уравнение (4) справедливо лишь до определенного предела.
Сегодня средний коэффициент смертности в наиболее развитых странах приближается к значению kd¥ » 0,01 год‑1, которое, по-видимому, определяется биологическим пределом продолжительности человеческой жизни. Соответственно, предельный уровень развития жизнесберегающих технологий есть p¥ = kd0‑kd¥ » 0,05 год‑1. Данное обстоятельство не означает ограниченности возможностей технологического развития вообще. Просто создаваемые технологии становятся все менее эффективными (по отношению, скажем, к их экономической значимости) с точки зрения спасения жизней.
Как следует из формулы (5), предельная численность человечества составляет N¥ = Cp¥ » 10 млрд.чел. Это значение не может быть превышено, поскольку избыток населения, не востребованный жизнесберегающими технологиями, будет неизбежно уничтожен. При этом способы устранения "лишних людей" могут быть самыми разными (войны, эпидемии, геноцид, крестовые походы, переселение народов).
УНИВЕРСАЛЬНЫЕ СИСТЕМНЫЕ МЕХАНИЗМЫ В ИСТОРИЧЕСКОЙ ДИНАМИКЕ
Единство всемирного исторического процесса, лежащее в основе многих историко-философских концепций, имеет количественное выражение. В соответствии с теорией Ф. Броделя, это относительное постоянство численности населения различных регионов [11]. Однако есть не менее важное свидетельство в пользу трактовки мира, как целостной развивающейся системы. Это степенной характер зависимостей, характеризующих систему расселения. Так, например, зависимость между числом жителей города и его рангом (номером в списке городов, упорядоченном в порядке убывания населения) представляет собой обратную пропорциональность (закон Ауэрбаха), т.е. имеет степенной вид (см. рис. 5). Такой же вид имеет зависимость ранг-размер для населения крупных стран (см. рис. 6).
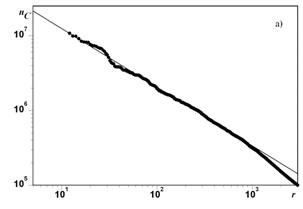
Рис. 5. Зависимость ранг-размер для городов, насчитывающих свыше 100 тыс. жителей
Степенная зависимость населения от ранга хорошо описывает порядка 30% крупнейших городов.
По данным [9].
Аналогичные степенные формулы известны в экономике (закон Парето), лингвистике (закон Эсту-Ципфа), наукометрии (законы Брэдфорда и Лотки) и ряде других областей. Степенной характер распределений говорит об отсутствии для рассматриваемых систем характерных масштабов, т.е. о сложности систем и наличии у них целостных свойств [12,13]. Можно предложить простое системное объяснение этого важного факта, построена и изучена соответствующая математическая модель.

Рис. 6. Зависимость ранг-размер для распределения стран по населению
Зависимость имеет степенной вид для пяти-шести десятков сотни крупнейших стран. Наблюдающееся далее отклонение от степенной зависимости можно интерпретировать как "нехватку" небольших стран или как недостаток населения в них.
По данным [10].
Развитие многих социально-экономических систем происходит таким образом, что скорость роста составляющих их объектов тем больше, чем больше сами объекты (по принципу "на деньгу деньга бежит"). Причем прирост, как правило, оказывается прямо пропорционален уже достигнутому уровню, т.е., с математической точки зрения, такие системы являются линейными. Вместе с тем, как известно, процессы самоорганизации, приводящие к сложному поведению, имеют место только в нелинейных системах (например, в отрытых нелинейных системах с локальными правилами степенные распределения могут возникать в результате самоорганизации в критическое состояние [12]). Таким образом, должен существовать механизм, обеспечивающий сложность линейных систем, не связанный с самоорганизацией.
Как было показано [7,14], для возникновения степенных распределений в линейных системах достаточно, чтобы их части обладали информацией об интегральных характеристиках системы. Иными словами, необходимо, чтобы система обладала "зачатками" целостности, которые в результате действия линейных механизмов "распространяются" на ее свойства. Таким образом, сложность может возникать либо в результате самоорганизации в нелинейных системах, либо в линейных системах с элементами целостности. Можно сказать, что целостность и нелинейность в каком-то смысле комплементарны.
Этот результат синергетики имеет для истории и ряда других гуманитарных дисциплин принципиальный характер. "Информация о целом", когда ей располагают отдельные элементы, становится "материальной силой". При этом сами элементы могут оказываться простейшими сущностями. Естественно, неверная информация о целом, может кардинально изменить свойства объекта, лишив его тех свойств, которыми он обладал бы при нормальном течении событий. Можно сказать, что выявленный системный механизм создает основу для анализа информационного управления обществом.
[Что ещё интересного в СО-сообществах 3-го круга:]_____________________________________________
Что ещё интересного в СО-сообществах 3-го круга:
2 Академия, Марсианский трактор, Мир Полдня, Школа Полдня, ЗОНА СИНГУЛЯРНОСТИ. 3geo + оЗадачник:
субъект "умный" очень легко поддаётся "магии толпы"
Экранизация проекта по использованию лунного ракетного топлива для вывода грузов с Земли и Марса
Картинка из будущего трансгуманизма от трансгуманиста
Оптическая иллюзия с восемью тираннозаврами
Основные положения теории четырёхмерного строения атома
"Точка G" мировой экономики
Шифрование в условиях древности
Историческая динамика. Взгляд с позиций синергетики
( Historical Dynamics. Synergetics Approach
Preprint, Inst. Appl. Math., the Russian Academy of Science)
Курдюмов С.П., Малинецкий Г.Г., Подлазов А.В.
(S.P.Kurdyumov, G.G.Malinetski, A.V.Podlazov)
ИПМ им. М.В.Келдыша РАН
Москва, 2004
Аннотация
В 1994 году была выдвинута исследовательская программа, связанная с построением теоретической истории. В основе этой программы лежало исследование возможных траекторий исторического развития с помощью компьютерного моделирования, широкого использования методов естественных и гуманитарных наук. Этот подход может сыграть исключительно важную роль с точки зрения стратегического планирования как на национальном, так и на глобального уровне. В последующие годы удалось существенно продвинуться в реализации междисциплинарного проекта, связанного с теоретической историей. Работа посвящена обсуждению нескольких принципиальных результатов, полученных в ходе этих исследований.
Abstract
The research program of theoretical history creation was put forward in 1994. This program was based on the investigation of possible historical development trajectories on basis by means of computer simulation, broad use of methods of natural and humanitarian sciences. This approach can be vary important from the point of view of the strategic planning on both national and global levels. During the ensuing years we succeeded in the realization of interdisciplinary project of theoretical history. Here we consider several fundamental results of these researches.
Со времен Ф. Броделя ведущим процессом в исторической науке стала дифференциация и специализация. Развивались экономическая история, историческая демография, историческая культурология, историческая география и т.д. Как и предсказывал французский исследователь, родились историческая психология и историческая социология. Сейчас настоятельно ощущается потребность в междисциплинарном синтезе, в подходах, позволяющих из множества аспектов, изучаемых различными науками, выделить главное, найти ключевые причинно-следственные связи и наиболее важные переменные.
В качестве основы для такого подхода наиболее естественно использовать теорию самоорганизации, или синергетику. Поэтому большой интерес представляют проекты, направленные на развитие своеобразного синергетического подхода в истории. Здесь возникает новый взгляд на традиционные исторические проблемы, связанный с реконструкцией прошедшего, с попыткой увидеть неожиданные, парадоксальные связи в событиях прошлого. И напротив, в событиях прошлого, кажущихся случайными и трудно объяснимыми, удается проследить универсальные системные механизмы. С другой стороны, создаваемые модели исторических процессов могут оказаться принципиально важными для анализа мировой динамики и для стратегического планирования.
При этом прошлое выступает как своеобразный полигон, обеспечивающий верификацию создаваемых концепций и математических описаний. Это позволяет взглянуть на историю не только как на ретроспективную науку, подобную астрономии или эволюционной биологии, где эксперимент невозможен и можно лишь восходить от следствий к причинам, но и как на перспективную, где существует и обратный ход - от выявленных при анализе исторического материала взаимосвязей, типичных сценариев событий к задачам прогноза.
ПАРАМЕТРЫ ПОРЯДКА В ИСТОРИЧЕСКИХ ПРОЦЕССАХ
Для использования представлений и методов синергетики принципиально наличие параметров порядка (одной или нескольких ведущих переменных, определяющих динамику всех остальных процессов). [1,2] Таим параметром при анализе многих исторических процессов является численность населения.
Математическое моделирование демографических процессов восходит еще к XVIII веку. Английский монах Мальтус сформулировал популяционный принцип. В соответствии с ним рост человечества описывается геометрической прогрессией, в то же время производство пищи растет по арифметической прогрессии. Исходя из этого принципа, Мальтус делал вывод о неизбежности войн, в которых будет истребляться значительная часть человечества.
Исследования профессора С.П. Капицы [3] показали, что Мальтус был неправ. В течение всей истории человечества его численность росла быстрее, чем по геометрической прогрессии, как утверждал Мальтус.
Она росла по гиперболическому закону
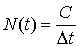
, (1)
где Dt = t‑2025, N - численность человечества, а C - постоянная, равная приблизительно 200 млрд. чел.×год. Это очень быстрый рост. К примеру, в 1700 году жителей на Земле было в 10 раз меньше, чем теперь. В начале царствования Петра I в России было всего 10 миллионов человек.

Рис. 1. Рост народонаселения мира
Графики, представляющие два различных сценария будущего развития, стремительно расходятся.
При сохранении тенденций, действовавших в течении всей предшествующей истории, численность человечества стала бы бесконечной приблизительно к 2025 г.
При демографическом переходе происходит замедление роста с вероятной стабилизаций народонаселения.
В настоящее время население мира растет на более чем на 1% в год при среднегодовом приросте свыше 70 миллионов человек.
Быстрый рост населения прежде всего в развивающихся странах в 50‑60‑е годы, во многом связанный с увеличением продолжительности жизни, обусловленной повышением качества медицинского обслуживания, получил название демографического взрыва.
В эти годы многие ученые считали, что ограничение численности населения в будущем будет связано с нехваткой продовольствия, поскольку и в настоящее время по данным ООН более 1 миллиарда человек голодает.
Однако ситуация оказалась совсем иной. Ученые, анализируя рост населения разных стран и мира в целом, столкнулись с важным и интересным явлением - демографическим переходом. Этот переход - постепенное изменение закона роста численности населения, замедление этого роста и последующая стабилизация численности (см. рис. 1 и рис. 2).

Рис. 2. Демографический переход
Прирост населения мира с 1750 по 2100 гг., усредненный за декады.
1 - развивающиеся страны, 2 - развитые.
Причем демографический переход происходит не в слаборазвитых странах, для которых характерны нехватка продовольствия и энергии, а в странах благополучных. Впервые демографический переход наблюдали в прошлом веке во Франции и Швеции. В настоящее время он произошел в большинстве европейских стран. В некоторых из них, например в Норвегии и Германии, рождаемость оказалась в последние десятилетия настолько низкой, что правительства этих стран начали активно привлекать иммигрантов для работы в ряде секторов экономики. Естественно, демографический переход кардинально меняет возрастную структуру общества (см. рис. 3). Продолжительность жизни возрастает, а население стареет, что непосредственно отражается на экономике и социальной структуре общества.

Рис. 3. Распределение населения мира по возрасту и полу в 1975 и 2000 г.г.
При демографическом переходе меняется возрастная структура.
Общество стареет, у него появляются новые проблемы.
Ожидающие нас в XXI веке изменения радикальны. Страна или город, в которых из десятилетия в десятилетие живет одно и то же число людей, должна иметь совсем другие технологии, другую мораль, другие культурные нормы. Банальнейший аналог здесь - средневековье, когда деревням было не под силу прокормить слишком большие города.
С позиций этой теории и теории режимов с обострением (пример величины, растущей в режиме с обострением дает закон (1)) [4], была проанализирована география расселения и выявлены условия, при которых возможно качественное изменение системы расселения - переход "экспансия-сосредоточение" [5,6]. Для миграции населения был введен некоторый феноменологический нелинейный закон. Проведенный анализ модели показал, что стадия экспансии, происходящей с уменьшением плотности населения, может быть характерна не для ослабленных этносов, как можно было бы предположить, а для обществ, имеющих большой потенциал развития. И затем случайные субъективные факторы могут прервать этот процесс, резко увеличив концентрацию населения в одном или нескольких городах или регионах.
ДЕМОГРАФИЧЕСКИЙ ПЕРЕХОД И ЖИЗНЕСБЕРЕГАЮЩИЕ ТЕХНОЛОГИИ
Нелинейность, присущая закону роста числа людей на планете, в соответствии с концепцией С.П. Капицы, обусловлена "информационным взаимодействием", действовавшим и миллион лет назад, и ныне. Эта теория имеет ряд внутренних трудностей и не объясняет непротиворечивым образом демографический переход, происходящий в последние десятилетия. Кроме того эта теория не позволяет выявить другие параметры порядка и предсказать траекторию мирового сообщества в случае их изменения.
В последние годы была развита альтернативная теория, связывающая нелинейность демографических процессов с развитием жизнесберегающих технологий (т.е. технологий, помогающих спасать людей и увеличивать продолжительность их жизни). С этих позиций, демографический переход связан с "насыщением" имеющихся технологий. На этой основе удается выявить системные механизмы гражданских войн, объяснить неоднократно наблюдавшийся в истории эффект "насыщения имперских технологий" (поздний Рим, крушение ряда других империй) и предсказать "полосу нестабильности", в которую вступает человечество в начавшемся веке. [7,8] Обсудим этот результат более подробно.
Формулу (1) можно переписать в виде дифференциального уравнения

. (2)
Его вид говорит о самоускоряющемся росте N или, что тоже самое, о сокращение масштаба времени, на котором происходят существенные демографические изменения, т.е. об ускорении хода истории.
Ключевым для описания процесса роста народонаселения является понятие жизнесберегающих технологий, под которыми понимаются любые знания, навыки или традиции, которые могут быть использованы для спасения человека от смерти или продления его жизни. Уровень развития жизнесберегающих технологий p будем характеризовать уменьшением среднего коэффициента смертности kd, достигнутым благодаря их действию, т.е. p = Dkd = kd ‑ kd0, гдеkd0 » 0,06 год‑1 коэффициент смертности первобытного человека. [7,8]
В предположении постоянства среднего коэффициента рождаемости для скорости роста народонаселения получаем уравнение
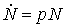
. (3)
Жизнесберегающие технологии не требуют для своего создания какого-то специального механизма. Являясь основой существования человечества, сутью человеческой культуры, они создаются людьми в процессе повседневной жизнедеятельности, т.е. на основе уже имеющихся жизнесберегающих технологий. Соответственно, для скорости их появления можно записать уравнение
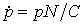
, (4)
константа C в котором определяет трудозатраты, необходимые на увеличение p в e раз при постоянном N.
Интегрируя систему (3)-(4), получаем основное уравнение теоретической демографии
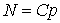
. (5)
Оно означает, что уровень развития жизнесберегающих технологий p, описывающий скорость роста народонаселения, характеризует в то же время размер экологической ниши человечества.
Может так случиться, что предписанный уравнением (5) баланс между уровнем жизнесберегающих технологий и населением по каким-то причинам где-то локально нарушается. Если в результате войн, эпидемий, стихийных бедствий и т.п. катаклизмов население уменьшается, то status quoвосстанавливается в течение всего лишь нескольких поколений. Если же, напротив, по каким-то причинам произошло чрезмерное увеличение численности населения, не сопровождаемое одновременным развитием технологий, то для появляющихся людей может просто не найтись места в социальной структуре общества, которая адекватна достигнутому уровню развития жизнесберегающих технологий. Возникающий при этом избыток людской численности обычно снимается посредством войн, которые в своем большинстве имеют демографическую, а не экономическую природу. [7,8]
Подстановка решения (5) в уравнение (3) немедленно приводит к уравнению (2), полученному ранее путем анализа демографических данных.

Рис. 4. Развитие технологий в последние века
В отличии от общего технологического уровня, уровень жизнесберегающих технологий выходит на насыщение.
Развитие жизнесберегающих имеет естественный предел, обусловленный тем, что нельзя спасти от смерти больше людей, чем их всего живет. Т.е. уровень жизнесберегающих технологий должен выйти на насыщение, в то время как рост общего технологического уровня будет продолжаться, как показано на рис. 4. Прекращение развития жизнесберегающих технологий означает, что уравнение (4) справедливо лишь до определенного предела.
Сегодня средний коэффициент смертности в наиболее развитых странах приближается к значению kd¥ » 0,01 год‑1, которое, по-видимому, определяется биологическим пределом продолжительности человеческой жизни. Соответственно, предельный уровень развития жизнесберегающих технологий есть p¥ = kd0‑kd¥ » 0,05 год‑1. Данное обстоятельство не означает ограниченности возможностей технологического развития вообще. Просто создаваемые технологии становятся все менее эффективными (по отношению, скажем, к их экономической значимости) с точки зрения спасения жизней.
Как следует из формулы (5), предельная численность человечества составляет N¥ = Cp¥ » 10 млрд.чел. Это значение не может быть превышено, поскольку избыток населения, не востребованный жизнесберегающими технологиями, будет неизбежно уничтожен. При этом способы устранения "лишних людей" могут быть самыми разными (войны, эпидемии, геноцид, крестовые походы, переселение народов).
УНИВЕРСАЛЬНЫЕ СИСТЕМНЫЕ МЕХАНИЗМЫ В ИСТОРИЧЕСКОЙ ДИНАМИКЕ
Единство всемирного исторического процесса, лежащее в основе многих историко-философских концепций, имеет количественное выражение. В соответствии с теорией Ф. Броделя, это относительное постоянство численности населения различных регионов [11]. Однако есть не менее важное свидетельство в пользу трактовки мира, как целостной развивающейся системы. Это степенной характер зависимостей, характеризующих систему расселения. Так, например, зависимость между числом жителей города и его рангом (номером в списке городов, упорядоченном в порядке убывания населения) представляет собой обратную пропорциональность (закон Ауэрбаха), т.е. имеет степенной вид (см. рис. 5). Такой же вид имеет зависимость ранг-размер для населения крупных стран (см. рис. 6).

Рис. 5. Зависимость ранг-размер для городов, насчитывающих свыше 100 тыс. жителей
Степенная зависимость населения от ранга хорошо описывает порядка 30% крупнейших городов.
По данным [9].
Аналогичные степенные формулы известны в экономике (закон Парето), лингвистике (закон Эсту-Ципфа), наукометрии (законы Брэдфорда и Лотки) и ряде других областей. Степенной характер распределений говорит об отсутствии для рассматриваемых систем характерных масштабов, т.е. о сложности систем и наличии у них целостных свойств [12,13]. Можно предложить простое системное объяснение этого важного факта, построена и изучена соответствующая математическая модель.

Рис. 6. Зависимость ранг-размер для распределения стран по населению
Зависимость имеет степенной вид для пяти-шести десятков сотни крупнейших стран. Наблюдающееся далее отклонение от степенной зависимости можно интерпретировать как "нехватку" небольших стран или как недостаток населения в них.
По данным [10].
Развитие многих социально-экономических систем происходит таким образом, что скорость роста составляющих их объектов тем больше, чем больше сами объекты (по принципу "на деньгу деньга бежит"). Причем прирост, как правило, оказывается прямо пропорционален уже достигнутому уровню, т.е., с математической точки зрения, такие системы являются линейными. Вместе с тем, как известно, процессы самоорганизации, приводящие к сложному поведению, имеют место только в нелинейных системах (например, в отрытых нелинейных системах с локальными правилами степенные распределения могут возникать в результате самоорганизации в критическое состояние [12]). Таким образом, должен существовать механизм, обеспечивающий сложность линейных систем, не связанный с самоорганизацией.
Как было показано [7,14], для возникновения степенных распределений в линейных системах достаточно, чтобы их части обладали информацией об интегральных характеристиках системы. Иными словами, необходимо, чтобы система обладала "зачатками" целостности, которые в результате действия линейных механизмов "распространяются" на ее свойства. Таким образом, сложность может возникать либо в результате самоорганизации в нелинейных системах, либо в линейных системах с элементами целостности. Можно сказать, что целостность и нелинейность в каком-то смысле комплементарны.
Этот результат синергетики имеет для истории и ряда других гуманитарных дисциплин принципиальный характер. "Информация о целом", когда ей располагают отдельные элементы, становится "материальной силой". При этом сами элементы могут оказываться простейшими сущностями. Естественно, неверная информация о целом, может кардинально изменить свойства объекта, лишив его тех свойств, которыми он обладал бы при нормальном течении событий. Можно сказать, что выявленный системный механизм создает основу для анализа информационного управления обществом.
[Что ещё интересного в СО-сообществах 3-го круга:]_____________________________________________
Что ещё интересного в СО-сообществах 3-го круга:
2 Академия, Марсианский трактор, Мир Полдня, Школа Полдня, ЗОНА СИНГУЛЯРНОСТИ. 3geo + оЗадачник:
субъект "умный" очень легко поддаётся "магии толпы"
Экранизация проекта по использованию лунного ракетного топлива для вывода грузов с Земли и Марса
Картинка из будущего трансгуманизма от трансгуманиста
Оптическая иллюзия с восемью тираннозаврами
Основные положения теории четырёхмерного строения атома
"Точка G" мировой экономики
Шифрование в условиях древности