Гари Поттер блин. неведомое.
однако что-то в Хогвартсе происходило литературно - математическое:

Гарри Поттер и волшебный форум → Ролевая игра Хогвартса → Хогвартс → Нумерология
http://www.harrypotter.com.ua/index.php?showtopic=62651
*Крики из кабинета Нумерологии были слышны даже в коридоре. Любопытней всего в них была личность кричащего - судя по густому баритону, это был мужчина. Однако такое поведение и такой голос ни мисс Дэвис, ни знакомому многим мистеру Гейбергу присущи не были. А значит, в гостях у профессора в этот раз оказался новый персонаж*
- Ты в диспут невступуема , твоя мысль не формируется ввиду отсутствия в ней содержания! - *горячился незнакомец* - Тебя всю жизнь учили дурре, а ты теперь дуррой детям мозги забиваешь. Это есть мировой заговор с целью отупления молодого поколения волшебников!
- Успокойся, Виктор, сейчас придут ученики, и ты сможешь рассказать им свою собственную теорию нумерологического валенка. И даже продемонстрировать опыты с картошкой и тухлой сельдью - я попросила домовиков принести продукты - *голос волшебницы был холоден как лед*
*Рискнувшим первыми заглянуть в кабинет ученикам, открылась бы удивительная картина: у доски стоял мужчина в мятой мантии, точно таких же брюках и грязных ботинках; лицо волшебника было подстать одежде - таким же мятым, сизым, плохо выбритым. Поверхности рабочего стола профессора не было видно из-за разложенных на ней картошки, нескольких сельдей, целого набора спиц и самых обычных маггловских валенок. А поверхность доски была сплошь исписана жуткого вида формулами, таблицами, графиками и диаграммами. Почерк не был знаком студентам - судя по всему, писал именно этот странный маг. Сама же Эйн занимала место за первой партой у окна. Почему чародейка позволила этому нервному волшебнику распоряжаться в ее кабинете, зачем разрешила занять свой стол, оставалось загадкой*
- Доброе утро - *с трудом перекрывая поток ругани незнакомца, поздоровалась с первыми прибывшими чародейка*
- Позвольте вам представить... моего коллегу из России - Виктора Григорьевича Татющика - *секундная заминка - и Эйн все же назвала имя, фамилию и отчество мага*
*Слово не хотело произноситься, слово упорно цеплялось за зубы и язык, слову упорно не хотелось срываться с губ девушки, но та все же нашла в себе силы назвать помятого коллегой*
- Он тоже занимается некоторыми проблемами Нумерологии...
- Что значит - тоже? Да я занимаюсь настоящей Нумерологией, а не той дурой, которую вы тут развели! - *снова напомнил о себе волшебник*
- Хорошо. Допустим - *профессор устало отерла рукой лоб* - Так вот, Виктор Григорьевич изложит вам свою собственную гипотезу...
- Не гипотезу, а научную концепцию!
- Так вот - *невозмутимо продолжала Эйн* - Изложит вам гипотезу и те, кто будет против ортодоксальной Нумерологии, попытаются доказать правоту взглядов мистера Татющика. Мы же с теми, кто за нее, попробуем отстоять честь официальной науки.
- Когда нумерологией занимаются дуры, настоящая научная концепция от этого сильно страдает, но когда дурость вдалбливается в ваши головы, это уже самое настоящее преступление. Ваши родители хотят видеть вас людьми образованными и развитыми, но разве знают они о том, какой бред вам тут подсовывают вместо настоящей науки? - *заняв место у центра доски, начал вещать маг*
*Голос у мужчины сразу стал монотонным и скучным, совсем не таким, каким он голосил всего пару минут назад. Голос усыплял внимательность, обволакивал и успокаивал. Слова вязкой патокой закупоривали уши, мешая думать, анализировать, оценивать*
- Во многих учебниках разные ученые дуры пишут, что числа бывают четными, нечетными, четно-четными, четно-нечетными, составными, несосотавными, совершенными, несовершенными, сверхсовершенными, треугольными, прямоугольными, пятиугольными и квадратными. Зачем вам вся эта галиматья? 1 - это число, 2 - это число, 3 - это число.
*Вооружившись мелом, волшебник принялся записывать числа на единственном свободном клочке доски*
- В записи 1 - это цифра, 2 - это цифра, 3 - это цифра. Цифра есть специальный знак для записи числа. И пришло к нам это слово из далекой Арабии, где словом «сыфыр» обозначали пустоту. Есть числа, а есть предназначенные для их записи знаки. Все! Треугольник, пятиугольник, квадрат и прямоугольник - это уже фигуры. Но ученые дуры считают не так. Ученые дуры считают, что эти числа есть сумма четных и четных, четных и нечетных, порядковых чисел. Ученая дура не знает, что те числа, которые она получает путем складывания ежа и кукурузы, будут самыми обычными четными или нечетными числами, относящимися к фигурам точно так же, как селедка относится к балалайке. Пифагор с его прихлебателями своим скудным умишком никак не мог понять, что числа и фигуры суть разные вещи. И потому властью, данной мне первым законом логики, я объявляю его сайнсфриком. Отныне Пифагор Самосский низложен и низвергнут от всякой научной принадлежности ибо чуда он безграмотная. Ну, а если вам в библиотеке какой папирус этой пифадуры попадется, то не судите строго, отпустите с миром ибо убогая она и в остальном беззлобная.
*Оба чародея внимательно слушали дискуссию студентов. Виктор - с ироничной ухмылкой, дескать, давайте, ребятки, играйте в бирюльки для дур. Эйн - внимательно, сосредоточенно, делая пометки на пергаменте*
- Что ж, думаю, фигурным числам внимания уделено достаточно, самое время поговорить о другой проблеме - проблеме единства нумерологических чисел - *на этот раз первой заговорила именно мисс Дэвис*
*Под недовольное фырканье Татющика и его колкие выпады в адрес ортодоксальной нумерологии и хогвартского нумеролога в частности, девушка продолжала*
- Мистер Татющик уверен, что целое обладает всеми свойствами его частей. Он уверен, что, например, число 11 будет обладать всеми свойствами единицы, правда, в двойном размере. А значит, рассматривать его отдельно в дате рождения нет никакого смысла. Точно так же дело обстоит и с числами третьего и прочих десятков, сотен, тысяч, да вообще со всеми числами, состоящими из двух и более "частей".
- И я тебе, дуре эдакой убогой, сейчас это докажу! - *вспылил долго сдерживающий естественные порывы к сквернословию маг*
*С этими словами он схватил стоящий на профессорском столе серебряный кубок*
- Здеся тыквенный сок - *зачем-то сообщил он студентам, и одним глотком осушил кубок*
- Вкусно, сладко - *резюмировался мужчина, рукавом вытирая испачканные оранжевым губы* - А теперь сделаем вот что.
*Отыскав на столе огромных размеров кубок, он перелил туда содержимое сразу трех кубков поменьше*
- Будет так же вкусно и сладко? Ну, давайте, попробуйте - *пригласил всех желающих на странную дегустацию волшебник*
- Потому что дурьи головы никак не возьмут в толк, что целое всегда обладает свойствами частей энтого самого целого. Вот и мудрят, и мудрят.
- Мне кажется, эта тема уже себя исчерпала, не так ли, коллега? - *глядя на порядком смущенных студентов, едва находящих в себе и силы и мужество на ответ, негромко проговорила Эйн*
*Впрочем, в само слово "коллега" она вложила как можно больше едкости и иронии - отношение мисс Дэвис к этому странному магу было понятно даже без слов*
- Вот! Вот она - типичная капитуляция ученой дурры! - *возликовал ее оппонент* - Стоит заговорить о настоящей науке, и вы сразу пытаетесь бежать от правды, как еретики от света инквизиторских костров!
- Положим, свет - это еще полбеды, а вот жар - проблема посерьезней - *все так же тихо парировала девушка* - Но выбор темы опять за Вами, мистер Татющик.
- Конечно, за мной. За мной и истинной наукой - *снова завелся мужчина* - А потому я сейчас докажу вам всю несостоятельность некоторых глупостей, которыми вам тут головы забивают. Вот, смотрите - это нумерологический валенок.
*С этими словами маг взял в руки самый обычный с виду валенок - серый, войлочный, совсем новый - недавно тот, похоже, был частью крепко скатанной пары - следы заломов еще были хорошо видны. Никакой особой нумерологичности в этом валенке видно не было*
- Этот валенок - основание любой системы счисления, назовем ее валенковой. Любое целое число в валенковой системе можно записать в виде.
*Мужчина подошел к доске и принялся быстро стучать по ней мелом, выписывая нужную формулу*

, где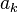
удовлетворяет неравенству
- Вас тут кормят баснями, что вавилонская нумерация есть первая позиционная система счисления в мире. Только она такой быть не может, потому что в ней нет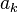
, равной нулю. Валенок есть, а нуля нет. Если валенок есть, значит он не ноль, а раз нет нуля - нет и никакой валенковой системы - неравенство не выполняется. Нет там такой цифры и все тут. Но ученые дурры не хотят смириться с собственной тупостью, вот и держатся за свои несостоятельные выводы - *торжествующе подвел итог своему выступлению волшебник*
Цитата
Мнение судьи
Обещанные итоги от нашего многоуважаемого судьи Clara Oswald. Споров они вызвали немало, однако, как отметила сама мисс Освальд, предложенные для практики темы были столь неоднозначны и сложны, что ответить на них просто "да" или "нет" порой было совсем непросто. Итак:
Предложенные для дискуссии темы интересны и актуальны для нумерологии, но, в то же время, и достаточно сложны, чтобы их можно было тщательно и подробно рассмотреть в рамках студенческой практики по предмету - ведь истина, как известно, не лежит на поверхности. Тем не менее, хотелось бы похвалить всех, кто проявил активность и принял участие в обсуждении. Среди аргументов, высказанных «за» или «против» той или иной точки зрения, были весьма оригинальные, свидетельствующие о нестандартном мышлении их авторов. Разумеется, степень их убедительности различна, не все из них мне лично кажутся верными. Однако, как сказал великий писатель и философ Антуан де Сент-Экзюпери, не высказывает ошибочных мыслей лишь тот, кто вообще не думает.
Теперь чуть подробнее и по сути. Участникам дискуссии были предложены следующие задания:
1. Доказать/опровергнуть существование треугольных, квадратных, пятиугольных и прямоугольных чисел.
2. Доказать/опровергнуть наличие у чисел старше первого десятка своих собственных нумерологических свойств, отличных от свойств их составляющих.
Что касается первого задания, то аргументация группы «против» показалась мне более логичной, последовательной и убедительной, независимо от того, как лично я отношусь к данному тезису. Группа «за», на мой взгляд, несколько увлеклась конкретными примерами, т.е. попытками «наглядно» продемонстрировать «фигурность» чисел, забывая при этом, что приписывание числам геометрической формы - это, в бОльшей степени, попытка понять их философскую суть, глубинное отличие одного от другого, чем просто указание на возможность разложить определенное количество предметов в виде каккой-то конкретной геометрической фигуры. Древнегреческие математики были философами, и, вряд ли, стали бы заниматься столь очевидными и банальными вещами. И да - речь идет именно о «приписывании» числу формы, а не об отождествлении числа с фигурой. Точно так же в современной физике кваркам приписывают «цвет» и «странность». Ведь число - это высшая степень абстракции по сравнению с геометрической фигурой, оно не может обладать какими-либо материальными свойствами, в принципе. Так что, группе «за», следовало бы вооружиться более глубокими, «философскими» аргументами в защиту своей точки зрения. Группа «против» нашла более убедительные аргументы, по крайней мере, на поверхности они выглядят именно так. Повторюсь еще раз - я здесь не обсуждаю правильность самих утверждений и не высказываю свое личное отношение к ним. Я просто оцениваю логичность и последовательность аргументов.
Цитата
Представим себе пять мячей, выстроенных не в единую линию, а так, чтобы каждый мяч представлял собой точку, составляющую пятиугольник. Мы увидим, что число "пять" перестает быть безликой цифрой в нумерации, а обретает форму, становится пятиугольным.Подобные действия можно проделать и с другими числами, переводя их в материальную плоскость, где они становятся зримыми и, можно сказать, обретают свое "тело" в виде определенной фигуры.
Никак не могу согласиться. Хотя бы потому, что в математике (а нумерология - это, можно сказать, ее родная сестра), конкретные примеры не являются доказательством правильности утверждения, а могут служить лишь для опровержения чего-либо. Доказательство должно проводиться в самом общем виде. Что я имею в виду? Даже если доказываемое утверждение верно для конкретных чисел (3, 5, 7 и т.п.), то это, строго говоря, не означает, что оно будет верно для любого натурального числа. А привести примеры для любого числа - не получится, ибо их - бесконечное множество.
Не могу не обратить внимание еще на один не вполне удачный аргумент группы «за»:
Цитата
Вернемся же к геометрическим числам, но прежде рассмотрим такую вещь, как вектор. Что есть вектор? Кто-то может сказать, что вектор - это прямой направленный отрезок, и он будет прав. Но несмотря на то, что это просто отрезок или как его еще можно назвать, просто направленная линия, с вектором можно производить различные операции. ... Любой вектор имеет свой модуль, а модуль - это число, соответственно любой вектор - это есть число.
При всем уважении к автору этой цитаты, я как математик, смею утверждать, что данная логическая цепочка неверна. Из того, что модуль вектора есть число, отнюдь не следует, что и вектор есть число. Модуль - это всего лишь одна из характеристик вектора, точно такая же, как и направление. В реальной жизни мы ведь не отождествляем какое-либо свойство предмета с ним самим.
Сходная логическая ошибка допущена и в рассуждении об эфире. Оставляя в стороне правильность или неправильность теории эфира, как основы всего сущего, остановлюсь на следующем утверждении:
«А как нам всем известно, атомный вес, плотность и другие свойства элементов являются абстрактными величинами, а, следовательно, они связаны с числами, соответственно эфир можно приравнять к числу.»
Из того, что какому-либо объекту (скажем так) присущи некоторые числовые характеристики, совершенно не следует, что его можно отождествлять с числом. Еще раз подчеркну: число - это абстракция, квинтэссенция количественной меры, как таковой, она не имеет и не может иметь материального воплощения.
А вот еще одно утверждение группы «за», показавшееся мне стоящим того, чтобы обратить на него внимание:
Цитата
1 - это точка, 2 точки, если их соединить - это линия (на которой и содержатся эти точки), 3 точки, если они не лежат на одной прямой - треугольник, и так далее.
Разумеется, с тем, что число 1 ассоциируется с точкой на плоскости, можно согласиться. Но вот дальше ... Отрезок никак нельзя сопоставить числу 2, равно как и треугольник - числу 3. Ну, и так далее. Ведь любая геометрическая фигура на плоскости, отличная от самой точки (и отрезок, в частности) это бесконечное множество точек, и автору цитаты это должно быть хорошо известно. Так что, никак нельзя сопоставлять н-угольники числам, если даже принять единицу за точку, как учил Аристотель.
Лично мне кажется, что стороннему наблюдателю довольно сложно согласиться с точкой зрения, доказательство которой сопровождается таким количеством ошибок и неточностей. Они ставят под сомнение и сам доказываемый тезис.
На фоне вышеприведенных рассуждений группы «за», рассуждения группы «против» выглядят хотя и проще, но зато логичнее.
Цитата
Единица - это точка, и у нее нет формы-фигуры, а следовательно она является безликой. Безликость - это фактически синоним абстрактности, что с легкостью опровергает теорию материальности чисел.
Звучит достаточно убедительно.
Цитата
Число можно записать по договоренности с другими представителями разумных самым немысленным способом. Да, зачем далеко ходить: вспомним систему исчисления древнего Египта и Вавилонии. Так чем в этом случае хуже фигуры? Ни чем. Следовательно выходит, что это очередная форма записи
В принципе, и с утверждением можно согласиться. Геометрическая фигура, как форма изображения числа. Действительно, чисто теоретически, можно провести такую аналогию, она не вызывает особых возражений.
Это только ключевые моменты дискуссии, которые мне лично бросились в глаза. Думаю, не имеет смысла анализировать каждую фразу каждого участника. Безусловно, у каждой стороны есть и удачные аргументы, и не очень, но аргументация группы «против» по данной теме, в целом, произвела на меня лучшее впечатление.
Перейдем ко второму заданию.
Честно говоря, для меня рассуждений было недостаточно, чтобы однозначно определить, чья аргументация лучше. И одна, и другая группа несколько ушли в сторону от темы задания. Лично я не очень уловила связь возникшей дискуссии с его первоначальной формулировкой. К чему тут возникший спор, являются ли слова «совершенный» и «идеальный» синонимами? От себя могу только добавить, что, например, в физике выражения «совершенная структура» и «идеальная структура» используются, как синонимы, ибо и одно и другое означает отсутствие дефектов, отклонений, чего-то лишнего. Последнее, кстати, перекликается с еще одной цитатой Экзюпери - «Совершенство достигается не тогда, когда уже нечего прибавить, но когда уже ничего нельзя отнять».
А вот использование кубков с тыквенным соком для доказательства/опровержения нумерологических концепций показалось мне весьма забавным и слегка разрядило напряженную атмосферу.
В целом, по данной теме аргументацию обеих групп (в плане ее убедительности) я оцениваю приблизительно на одном уровне.
Делать выводы из сказанного мной предоставляю уважаемому профессору.
Внимательно изучив доводы судьи и проанализировав работу каждой из групп, я пришла к выводу, что обе в равной степени заслужили победу. Иногда одна из них была более убедительной, а другая - менее. Иногда одна из групп была активнее, предпочитая быть пассивной в другое время. Но! Тот факт, что каждая из групп работала, анализировала, строила гипотезы и выдвигала собственные теории, наиболее ценен. А любой труд, особенно настолько непростой, как на этой практике, достоин уважения и награды. Как сказали бы магглы, победила дружба.

Гарри Поттер и волшебный форум → Ролевая игра Хогвартса → Хогвартс → Нумерология
http://www.harrypotter.com.ua/index.php?showtopic=62651
*Крики из кабинета Нумерологии были слышны даже в коридоре. Любопытней всего в них была личность кричащего - судя по густому баритону, это был мужчина. Однако такое поведение и такой голос ни мисс Дэвис, ни знакомому многим мистеру Гейбергу присущи не были. А значит, в гостях у профессора в этот раз оказался новый персонаж*
- Ты в диспут невступуема , твоя мысль не формируется ввиду отсутствия в ней содержания! - *горячился незнакомец* - Тебя всю жизнь учили дурре, а ты теперь дуррой детям мозги забиваешь. Это есть мировой заговор с целью отупления молодого поколения волшебников!
- Успокойся, Виктор, сейчас придут ученики, и ты сможешь рассказать им свою собственную теорию нумерологического валенка. И даже продемонстрировать опыты с картошкой и тухлой сельдью - я попросила домовиков принести продукты - *голос волшебницы был холоден как лед*
*Рискнувшим первыми заглянуть в кабинет ученикам, открылась бы удивительная картина: у доски стоял мужчина в мятой мантии, точно таких же брюках и грязных ботинках; лицо волшебника было подстать одежде - таким же мятым, сизым, плохо выбритым. Поверхности рабочего стола профессора не было видно из-за разложенных на ней картошки, нескольких сельдей, целого набора спиц и самых обычных маггловских валенок. А поверхность доски была сплошь исписана жуткого вида формулами, таблицами, графиками и диаграммами. Почерк не был знаком студентам - судя по всему, писал именно этот странный маг. Сама же Эйн занимала место за первой партой у окна. Почему чародейка позволила этому нервному волшебнику распоряжаться в ее кабинете, зачем разрешила занять свой стол, оставалось загадкой*
- Доброе утро - *с трудом перекрывая поток ругани незнакомца, поздоровалась с первыми прибывшими чародейка*
- Позвольте вам представить... моего коллегу из России - Виктора Григорьевича Татющика - *секундная заминка - и Эйн все же назвала имя, фамилию и отчество мага*
*Слово не хотело произноситься, слово упорно цеплялось за зубы и язык, слову упорно не хотелось срываться с губ девушки, но та все же нашла в себе силы назвать помятого коллегой*
- Он тоже занимается некоторыми проблемами Нумерологии...
- Что значит - тоже? Да я занимаюсь настоящей Нумерологией, а не той дурой, которую вы тут развели! - *снова напомнил о себе волшебник*
- Хорошо. Допустим - *профессор устало отерла рукой лоб* - Так вот, Виктор Григорьевич изложит вам свою собственную гипотезу...
- Не гипотезу, а научную концепцию!
- Так вот - *невозмутимо продолжала Эйн* - Изложит вам гипотезу и те, кто будет против ортодоксальной Нумерологии, попытаются доказать правоту взглядов мистера Татющика. Мы же с теми, кто за нее, попробуем отстоять честь официальной науки.
- Когда нумерологией занимаются дуры, настоящая научная концепция от этого сильно страдает, но когда дурость вдалбливается в ваши головы, это уже самое настоящее преступление. Ваши родители хотят видеть вас людьми образованными и развитыми, но разве знают они о том, какой бред вам тут подсовывают вместо настоящей науки? - *заняв место у центра доски, начал вещать маг*
*Голос у мужчины сразу стал монотонным и скучным, совсем не таким, каким он голосил всего пару минут назад. Голос усыплял внимательность, обволакивал и успокаивал. Слова вязкой патокой закупоривали уши, мешая думать, анализировать, оценивать*
- Во многих учебниках разные ученые дуры пишут, что числа бывают четными, нечетными, четно-четными, четно-нечетными, составными, несосотавными, совершенными, несовершенными, сверхсовершенными, треугольными, прямоугольными, пятиугольными и квадратными. Зачем вам вся эта галиматья? 1 - это число, 2 - это число, 3 - это число.
*Вооружившись мелом, волшебник принялся записывать числа на единственном свободном клочке доски*
- В записи 1 - это цифра, 2 - это цифра, 3 - это цифра. Цифра есть специальный знак для записи числа. И пришло к нам это слово из далекой Арабии, где словом «сыфыр» обозначали пустоту. Есть числа, а есть предназначенные для их записи знаки. Все! Треугольник, пятиугольник, квадрат и прямоугольник - это уже фигуры. Но ученые дуры считают не так. Ученые дуры считают, что эти числа есть сумма четных и четных, четных и нечетных, порядковых чисел. Ученая дура не знает, что те числа, которые она получает путем складывания ежа и кукурузы, будут самыми обычными четными или нечетными числами, относящимися к фигурам точно так же, как селедка относится к балалайке. Пифагор с его прихлебателями своим скудным умишком никак не мог понять, что числа и фигуры суть разные вещи. И потому властью, данной мне первым законом логики, я объявляю его сайнсфриком. Отныне Пифагор Самосский низложен и низвергнут от всякой научной принадлежности ибо чуда он безграмотная. Ну, а если вам в библиотеке какой папирус этой пифадуры попадется, то не судите строго, отпустите с миром ибо убогая она и в остальном беззлобная.
*Оба чародея внимательно слушали дискуссию студентов. Виктор - с ироничной ухмылкой, дескать, давайте, ребятки, играйте в бирюльки для дур. Эйн - внимательно, сосредоточенно, делая пометки на пергаменте*
- Что ж, думаю, фигурным числам внимания уделено достаточно, самое время поговорить о другой проблеме - проблеме единства нумерологических чисел - *на этот раз первой заговорила именно мисс Дэвис*
*Под недовольное фырканье Татющика и его колкие выпады в адрес ортодоксальной нумерологии и хогвартского нумеролога в частности, девушка продолжала*
- Мистер Татющик уверен, что целое обладает всеми свойствами его частей. Он уверен, что, например, число 11 будет обладать всеми свойствами единицы, правда, в двойном размере. А значит, рассматривать его отдельно в дате рождения нет никакого смысла. Точно так же дело обстоит и с числами третьего и прочих десятков, сотен, тысяч, да вообще со всеми числами, состоящими из двух и более "частей".
- И я тебе, дуре эдакой убогой, сейчас это докажу! - *вспылил долго сдерживающий естественные порывы к сквернословию маг*
*С этими словами он схватил стоящий на профессорском столе серебряный кубок*
- Здеся тыквенный сок - *зачем-то сообщил он студентам, и одним глотком осушил кубок*
- Вкусно, сладко - *резюмировался мужчина, рукавом вытирая испачканные оранжевым губы* - А теперь сделаем вот что.
*Отыскав на столе огромных размеров кубок, он перелил туда содержимое сразу трех кубков поменьше*
- Будет так же вкусно и сладко? Ну, давайте, попробуйте - *пригласил всех желающих на странную дегустацию волшебник*
- Потому что дурьи головы никак не возьмут в толк, что целое всегда обладает свойствами частей энтого самого целого. Вот и мудрят, и мудрят.
- Мне кажется, эта тема уже себя исчерпала, не так ли, коллега? - *глядя на порядком смущенных студентов, едва находящих в себе и силы и мужество на ответ, негромко проговорила Эйн*
*Впрочем, в само слово "коллега" она вложила как можно больше едкости и иронии - отношение мисс Дэвис к этому странному магу было понятно даже без слов*
- Вот! Вот она - типичная капитуляция ученой дурры! - *возликовал ее оппонент* - Стоит заговорить о настоящей науке, и вы сразу пытаетесь бежать от правды, как еретики от света инквизиторских костров!
- Положим, свет - это еще полбеды, а вот жар - проблема посерьезней - *все так же тихо парировала девушка* - Но выбор темы опять за Вами, мистер Татющик.
- Конечно, за мной. За мной и истинной наукой - *снова завелся мужчина* - А потому я сейчас докажу вам всю несостоятельность некоторых глупостей, которыми вам тут головы забивают. Вот, смотрите - это нумерологический валенок.
*С этими словами маг взял в руки самый обычный с виду валенок - серый, войлочный, совсем новый - недавно тот, похоже, был частью крепко скатанной пары - следы заломов еще были хорошо видны. Никакой особой нумерологичности в этом валенке видно не было*
- Этот валенок - основание любой системы счисления, назовем ее валенковой. Любое целое число в валенковой системе можно записать в виде.
*Мужчина подошел к доске и принялся быстро стучать по ней мелом, выписывая нужную формулу*

, где
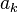
удовлетворяет неравенству

- Вас тут кормят баснями, что вавилонская нумерация есть первая позиционная система счисления в мире. Только она такой быть не может, потому что в ней нет
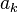
, равной нулю. Валенок есть, а нуля нет. Если валенок есть, значит он не ноль, а раз нет нуля - нет и никакой валенковой системы - неравенство не выполняется. Нет там такой цифры и все тут. Но ученые дурры не хотят смириться с собственной тупостью, вот и держатся за свои несостоятельные выводы - *торжествующе подвел итог своему выступлению волшебник*
Цитата
Мнение судьи
Обещанные итоги от нашего многоуважаемого судьи Clara Oswald. Споров они вызвали немало, однако, как отметила сама мисс Освальд, предложенные для практики темы были столь неоднозначны и сложны, что ответить на них просто "да" или "нет" порой было совсем непросто. Итак:
Предложенные для дискуссии темы интересны и актуальны для нумерологии, но, в то же время, и достаточно сложны, чтобы их можно было тщательно и подробно рассмотреть в рамках студенческой практики по предмету - ведь истина, как известно, не лежит на поверхности. Тем не менее, хотелось бы похвалить всех, кто проявил активность и принял участие в обсуждении. Среди аргументов, высказанных «за» или «против» той или иной точки зрения, были весьма оригинальные, свидетельствующие о нестандартном мышлении их авторов. Разумеется, степень их убедительности различна, не все из них мне лично кажутся верными. Однако, как сказал великий писатель и философ Антуан де Сент-Экзюпери, не высказывает ошибочных мыслей лишь тот, кто вообще не думает.
Теперь чуть подробнее и по сути. Участникам дискуссии были предложены следующие задания:
1. Доказать/опровергнуть существование треугольных, квадратных, пятиугольных и прямоугольных чисел.
2. Доказать/опровергнуть наличие у чисел старше первого десятка своих собственных нумерологических свойств, отличных от свойств их составляющих.
Что касается первого задания, то аргументация группы «против» показалась мне более логичной, последовательной и убедительной, независимо от того, как лично я отношусь к данному тезису. Группа «за», на мой взгляд, несколько увлеклась конкретными примерами, т.е. попытками «наглядно» продемонстрировать «фигурность» чисел, забывая при этом, что приписывание числам геометрической формы - это, в бОльшей степени, попытка понять их философскую суть, глубинное отличие одного от другого, чем просто указание на возможность разложить определенное количество предметов в виде каккой-то конкретной геометрической фигуры. Древнегреческие математики были философами, и, вряд ли, стали бы заниматься столь очевидными и банальными вещами. И да - речь идет именно о «приписывании» числу формы, а не об отождествлении числа с фигурой. Точно так же в современной физике кваркам приписывают «цвет» и «странность». Ведь число - это высшая степень абстракции по сравнению с геометрической фигурой, оно не может обладать какими-либо материальными свойствами, в принципе. Так что, группе «за», следовало бы вооружиться более глубокими, «философскими» аргументами в защиту своей точки зрения. Группа «против» нашла более убедительные аргументы, по крайней мере, на поверхности они выглядят именно так. Повторюсь еще раз - я здесь не обсуждаю правильность самих утверждений и не высказываю свое личное отношение к ним. Я просто оцениваю логичность и последовательность аргументов.
Цитата
Представим себе пять мячей, выстроенных не в единую линию, а так, чтобы каждый мяч представлял собой точку, составляющую пятиугольник. Мы увидим, что число "пять" перестает быть безликой цифрой в нумерации, а обретает форму, становится пятиугольным.Подобные действия можно проделать и с другими числами, переводя их в материальную плоскость, где они становятся зримыми и, можно сказать, обретают свое "тело" в виде определенной фигуры.
Никак не могу согласиться. Хотя бы потому, что в математике (а нумерология - это, можно сказать, ее родная сестра), конкретные примеры не являются доказательством правильности утверждения, а могут служить лишь для опровержения чего-либо. Доказательство должно проводиться в самом общем виде. Что я имею в виду? Даже если доказываемое утверждение верно для конкретных чисел (3, 5, 7 и т.п.), то это, строго говоря, не означает, что оно будет верно для любого натурального числа. А привести примеры для любого числа - не получится, ибо их - бесконечное множество.
Не могу не обратить внимание еще на один не вполне удачный аргумент группы «за»:
Цитата
Вернемся же к геометрическим числам, но прежде рассмотрим такую вещь, как вектор. Что есть вектор? Кто-то может сказать, что вектор - это прямой направленный отрезок, и он будет прав. Но несмотря на то, что это просто отрезок или как его еще можно назвать, просто направленная линия, с вектором можно производить различные операции. ... Любой вектор имеет свой модуль, а модуль - это число, соответственно любой вектор - это есть число.
При всем уважении к автору этой цитаты, я как математик, смею утверждать, что данная логическая цепочка неверна. Из того, что модуль вектора есть число, отнюдь не следует, что и вектор есть число. Модуль - это всего лишь одна из характеристик вектора, точно такая же, как и направление. В реальной жизни мы ведь не отождествляем какое-либо свойство предмета с ним самим.
Сходная логическая ошибка допущена и в рассуждении об эфире. Оставляя в стороне правильность или неправильность теории эфира, как основы всего сущего, остановлюсь на следующем утверждении:
«А как нам всем известно, атомный вес, плотность и другие свойства элементов являются абстрактными величинами, а, следовательно, они связаны с числами, соответственно эфир можно приравнять к числу.»
Из того, что какому-либо объекту (скажем так) присущи некоторые числовые характеристики, совершенно не следует, что его можно отождествлять с числом. Еще раз подчеркну: число - это абстракция, квинтэссенция количественной меры, как таковой, она не имеет и не может иметь материального воплощения.
А вот еще одно утверждение группы «за», показавшееся мне стоящим того, чтобы обратить на него внимание:
Цитата
1 - это точка, 2 точки, если их соединить - это линия (на которой и содержатся эти точки), 3 точки, если они не лежат на одной прямой - треугольник, и так далее.
Разумеется, с тем, что число 1 ассоциируется с точкой на плоскости, можно согласиться. Но вот дальше ... Отрезок никак нельзя сопоставить числу 2, равно как и треугольник - числу 3. Ну, и так далее. Ведь любая геометрическая фигура на плоскости, отличная от самой точки (и отрезок, в частности) это бесконечное множество точек, и автору цитаты это должно быть хорошо известно. Так что, никак нельзя сопоставлять н-угольники числам, если даже принять единицу за точку, как учил Аристотель.
Лично мне кажется, что стороннему наблюдателю довольно сложно согласиться с точкой зрения, доказательство которой сопровождается таким количеством ошибок и неточностей. Они ставят под сомнение и сам доказываемый тезис.
На фоне вышеприведенных рассуждений группы «за», рассуждения группы «против» выглядят хотя и проще, но зато логичнее.
Цитата
Единица - это точка, и у нее нет формы-фигуры, а следовательно она является безликой. Безликость - это фактически синоним абстрактности, что с легкостью опровергает теорию материальности чисел.
Звучит достаточно убедительно.
Цитата
Число можно записать по договоренности с другими представителями разумных самым немысленным способом. Да, зачем далеко ходить: вспомним систему исчисления древнего Египта и Вавилонии. Так чем в этом случае хуже фигуры? Ни чем. Следовательно выходит, что это очередная форма записи
В принципе, и с утверждением можно согласиться. Геометрическая фигура, как форма изображения числа. Действительно, чисто теоретически, можно провести такую аналогию, она не вызывает особых возражений.
Это только ключевые моменты дискуссии, которые мне лично бросились в глаза. Думаю, не имеет смысла анализировать каждую фразу каждого участника. Безусловно, у каждой стороны есть и удачные аргументы, и не очень, но аргументация группы «против» по данной теме, в целом, произвела на меня лучшее впечатление.
Перейдем ко второму заданию.
Честно говоря, для меня рассуждений было недостаточно, чтобы однозначно определить, чья аргументация лучше. И одна, и другая группа несколько ушли в сторону от темы задания. Лично я не очень уловила связь возникшей дискуссии с его первоначальной формулировкой. К чему тут возникший спор, являются ли слова «совершенный» и «идеальный» синонимами? От себя могу только добавить, что, например, в физике выражения «совершенная структура» и «идеальная структура» используются, как синонимы, ибо и одно и другое означает отсутствие дефектов, отклонений, чего-то лишнего. Последнее, кстати, перекликается с еще одной цитатой Экзюпери - «Совершенство достигается не тогда, когда уже нечего прибавить, но когда уже ничего нельзя отнять».
А вот использование кубков с тыквенным соком для доказательства/опровержения нумерологических концепций показалось мне весьма забавным и слегка разрядило напряженную атмосферу.
В целом, по данной теме аргументацию обеих групп (в плане ее убедительности) я оцениваю приблизительно на одном уровне.
Делать выводы из сказанного мной предоставляю уважаемому профессору.
Внимательно изучив доводы судьи и проанализировав работу каждой из групп, я пришла к выводу, что обе в равной степени заслужили победу. Иногда одна из них была более убедительной, а другая - менее. Иногда одна из групп была активнее, предпочитая быть пассивной в другое время. Но! Тот факт, что каждая из групп работала, анализировала, строила гипотезы и выдвигала собственные теории, наиболее ценен. А любой труд, особенно настолько непростой, как на этой практике, достоин уважения и награды. Как сказали бы магглы, победила дружба.