Новое доказательство иррациональности некоторых квадратных корней
Новое доказательство иррациональности некоторых квадратных корней
Недавно читал запоздало 9-й номер за 2012 год "Математики в школе". Приглянулась статья Л.А. Штейнгарца "НОВЫЕ ДОКАЗАТЕЛЬСТВА ИРРАЦИОНАЛЬНОСТИ ЧИСЕЛ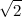
И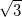
ИЛИ О ТОМ, КАК ПОСЛЕДНИЕ ЦИФРЫ ЧИСЛА ПОМОГАЮТ РЕШАТЬ ЗАДАЧИ.
Допустим, что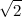
рациональное число. Тогда существуют целые взаимно простые числа m и n такие, что
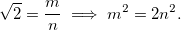
(1)
Рассмотрим последнюю цифру числа m2. Так как это квадрат некоторого натурального числа, то число m2 может оканчиваться лишь одной из следующих цифр: 0, 1, 4, 5, 6 или 9. (2)
Именно этими цифрами оканчиваются квадраты однозначных чисел. А следовательно, и всех натуральных.
Последняя цифра в десятичной записи другого квадрата - числа n2 - также одна из этих шести цифр. Но тогда число 2n2 может оканчиваться лишь одной из трех цифр 0, 2 или 8. (3)
Совершенно ясно, что равенство (1) возможно в единственном случае, когда оба числа m2 и 2n2 оканчиваются нулем. Это единственная общая цифра наборов (2) и (3). Но в этом случае каждое из чисел m и п должно делиться на 5, а это противоречит несократимости дроби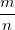
.
Мы пришли к противоречию. Следовательно, наше допущение неверно, и число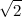
- иррациональное.
Аналогично и легко доказывается иррациональность, к примеру,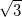
или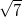
.
Оригинал взят у janka_x
Недавно читал запоздало 9-й номер за 2012 год "Математики в школе". Приглянулась статья Л.А. Штейнгарца "НОВЫЕ ДОКАЗАТЕЛЬСТВА ИРРАЦИОНАЛЬНОСТИ ЧИСЕЛ
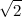
И
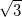
ИЛИ О ТОМ, КАК ПОСЛЕДНИЕ ЦИФРЫ ЧИСЛА ПОМОГАЮТ РЕШАТЬ ЗАДАЧИ.
Допустим, что
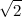
рациональное число. Тогда существуют целые взаимно простые числа m и n такие, что
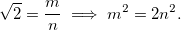
(1)
Рассмотрим последнюю цифру числа m2. Так как это квадрат некоторого натурального числа, то число m2 может оканчиваться лишь одной из следующих цифр: 0, 1, 4, 5, 6 или 9. (2)
Именно этими цифрами оканчиваются квадраты однозначных чисел. А следовательно, и всех натуральных.
Последняя цифра в десятичной записи другого квадрата - числа n2 - также одна из этих шести цифр. Но тогда число 2n2 может оканчиваться лишь одной из трех цифр 0, 2 или 8. (3)
Совершенно ясно, что равенство (1) возможно в единственном случае, когда оба числа m2 и 2n2 оканчиваются нулем. Это единственная общая цифра наборов (2) и (3). Но в этом случае каждое из чисел m и п должно делиться на 5, а это противоречит несократимости дроби
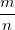
.
Мы пришли к противоречию. Следовательно, наше допущение неверно, и число
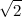
- иррациональное.
Аналогично и легко доказывается иррациональность, к примеру,
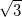
или
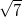
.
Оригинал взят у janka_x