Задача о поверхности сферы. Решение предыдущей задачи
Все ответившие получают неуд по теории групп :)
Представим углы треугольника в виде (pi/l, pi/m, pi/n).
Углы одного треугольника на поверхности сферы в сумме всегда дают значение превышающее pi. Кроме того, их сумма зависит от соотношения площади треугольника к площади сферы (что видимо всех и запутало, когда делили арбуз).
Это значит, что их сумма должна удовлетворять неравенству:

Целочисленные решения представленны наглядно ниже:
Три таких случая:
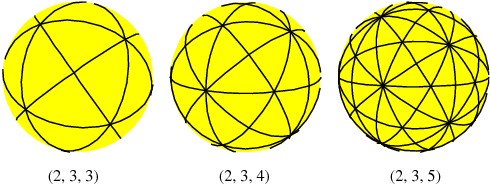
И один такой случай:

Правда один из его углов может быть любым целым числом более или равным 2, например 3:

Нецелочисленные случаи так же ограниченны:
(2 3 3), (2 3/2 3), (2 3/2 3/2), (3/2 3 3), (3/2 3/2 3/2)
(2 3 4), (2 3/2 4), (2 3 4/3), (2 3/2 4/3), (3/2 4 4), (3 4/3 4), (3/2 4/3 4/3)
(2 3 5), (2 3/2 5), (2 3 5/4), (2 3/2 5/4),(2 5/2 5), (2 5/3 5), (2 5/2 5/4), (2 5/3 5/4), (2 5/2 3), (2 5/3 3), (2 5/2 3/2), (2 5/3 3/2)
(5/2 3 3), (5/3 3/2 3), (5/2 3/2 3/2), (3/2 5 5), (3 5/4 5), (3/2 5/4 5/4), (5/2 5/2 5/2), (5/3 5/3 5/2), (3/2 3 5), (3 3 5/4), (3/2 3/2 5/4), (5/4 5 5), (5/4 5/4 5/4), (5/3 5/2 3), (5/2 5/2 3/2), (5/3 5/3 3/2)
UPD:
1) т.к. для соответствия заданию требуются равные друг другу многоугольники, то кол-во вариантов можно ещё сократить, оставив только случаи где два угла равны друг другу, т.е. типа (X X Y).
2) требуется доказать, что они покроют всю сферу без накладок или отверстий
А вот некоторые примеры не только треугольников, но я сомневаюсь что эти многоугольники равны:
Футбольный мяч, волейбольный мяч.
UPD2: про футбольный мяч я конечно сморозил :)