Краткая история солитона: заметки к юбилею
Повторяю запись, опубликованную пятнадцать лет назад, заменив 175 на 190.
- Известны случаи, когда обычная прогулка приводила к неожиданным последствиям, благодаря которым надолго, если не навсегда, входила в историю. Далеко ходить за примером не надо - через три года будем отмечать стопятидесятилетие той лодочной прогулки, из которой выросла сказка об Алисе.
- Нередко соавторами научных открытий становились животные. Я не о вечных мучениках науки - лабораторных лягушках, мышах, собаках. Я имею в виду именно соавторов - скажем, кота, который, прыгнув на стол и опрокинув колбы, помог своему хозяину Бернару Куртуа открыть химический элемент йод.
- Порой авторы открытий, литературных или музыкальных произведений, добившись однажды выдающегося успеха, потом больше ничем себя не проявляли и уходили в глубокую тень. Не зря Стефан Цвейг назвал свою повесть об авторе "Марсельезы" Гений одной ночи.
- Часто случается так, что удачно, казалось бы, подобранное название или имя авторам приходится менять во избежание судебных исков. К примеру, один и тот же персонаж Марка Твена по фамилии Селлерс именовался поочередно Эшколом, Бирайей и только потом окончательно стал Малберри.
Эти истории - с некоторой натяжкой, конечно - могут послужить и для того, чтобы обсудить открытие, 190-я годовщина которого отмечается в эти дни.

Шотландский инженер-кораблестроитель Джон Скотт Рассел (1808-1882) занимался исследованиями на канале Union Canal близ Эдинбурга. В те времена баржи еще водили лошади, и Рассел исследовал возможность замены конной тяги на паровую, изучал движение судов разного размера и формы.
И вот однажды близ Hermiston Experimental Station (в шести милях от центра Эдинбурга) случилось... Впрочем, дадим слово самому Расселу:
Я следил за движением баржи, которую быстро тянула по узкому каналу пара лошадей, когда баржа неожиданно остановилась. Но масса воды, которую баржа привела в движение, собралась около носа судна в состоянии бешеного движения, затем неожиданно оставила его позади, катясь вперед с огромной скоростью и принимая форму большого одиночного возвышения - округлого, гладкого и четко выраженного водяного холма. Он продолжал свой путь вдоль канала, нисколько не меняя своей формы и не снижая скорости. Я последовал за ним верхом, и когда нагнал его, он по-прежнему катился вперед со скоростью примерно 8-9 миль в час, сохранив свой первоначальный профиль возвышения длиной около тридцати футов и высотой от фута до полутора футов. Его высота постепенно уменьшалась, и после одной или двух миль погони я потерял его в изгибах канала. Так в августе месяце 1834 года произошла моя первая случайная встреча с этим необыкновенным и прекрасным явлением, которое я назвал Волной Переноса [в других переводах - Волной Трансляции - В.З.].
J. Scott Russell. Report on waves,
Fourteenth meeting of the British Association for the Advancement of Science, 1844
Вот так три лошади помогли пронаблюдать принципиально новое явление. Рассел продолжил эксперименты, выбирал баржи разного размера и формы. Он установил зависимость скорости этой волны от ее высоты, выяснил, что эти волны стабильны и, в отличие от обычных, не расплываются, перемещаясь на большие расстояния.

В 1982 году на конференции, приуроченной к столетию со дня смерти Джона Скотта Рассела, попытались воспроизвести его первый опыт. В том же месте того же канала такую же баржу влекли те же лошади нет, уже не лошади, а люди. И ничего не получилось! Волну воспроизвести не удалось. Попытку повторили в 1995 году на акведуке, названном именем Рассела - и на сей раз она удалась, результат вы видите на снимке справа.
Результаты через десять лет Рассел обобщил в сообщении Report of Waves (книгу можно скачать на Google Books). Дать математическое описание этого явления он не смог - открытие очень уж опередило свое время - и обратился к своей основной специальности, став известным кораблестроителем. Помимо прочего, он принимал деятельное участие в создании знаменитого корабля "Грейт Истерн", который вошел в историю не только техники, но и литературы. Именно знакомство с ним побудило Жюля Верна написать романы Плавающий город иПлавучий остров. Стефан Цвейг повесть Первое слово из-за океана из цикла "Звездные часы человечества" посвятил прокладке первого трансатлантического кабеля, которая оказалась возможной именно благодаря гиганту "Грейт Истерн", а главный участник и вдохновитель этого Сайрус Филд стал одним из прототипов Сайруса Смита из Таинственного острова того же Верна. Не забудем, конечно, и Левиафан Бориса Акунина.
В конце жизни Рассел вернулся к исследованиям волны переноса, попытавшись даже оценить своим методом толщину атмосферы и размеры Вселенной. Но точная математическая интерпретация явления была дана только после его смерти.


Diederik Johannes Korteweg
(1848-1941)Gustav de Vries
(1866-1934 )
В 1894 году голландец Густав де Фриз под руководством Дидерика Кортевега написал диссертацию, результатом которой стала их совместная статья On the Change of Form of Long Waves advancing in a Rectangular Canal and on a New Type of Long Stationary Waves. Уравнение, решение которого было получено в работе, получило название уравнения Кортевега-де Фриза и по традиции сокращается как KdV или КдФ. Именно это уравнение описывает волну Рассела и объясняет ее поведение. Не хочется забивать читателю голову математикой, но здесь от нее никуда не денешься:
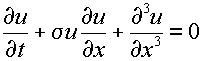
Это уравнение означает, что в среде, в которой возможна волна Рассела, действуют два конкурирующих механизма: нелинейность и дисперсия. Нелинейность (второе слагаемое уравнения) приводит к тому, что скорость точки волны тем больше, чем ближе эта точка находится к вершине и чем дальше она от подножия:
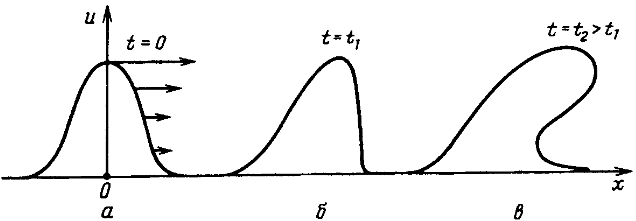
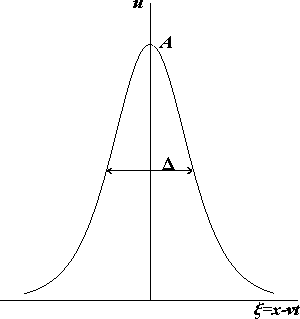
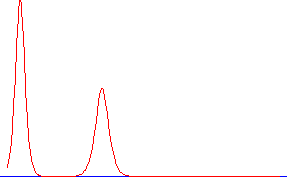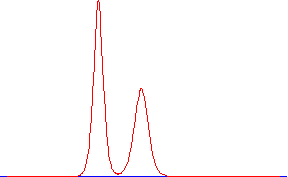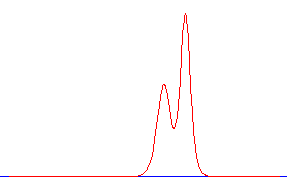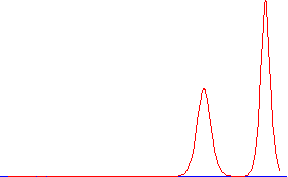
В результате вершина как бы обгоняет подножие, фронт волны становится круче и в конце концов волна может опрокинуться. Трагическим примером такого сценария могут послужить события 1999 года на Немиге. Дисперсия(третье слагаемое уравнения; не станем вдаваться в подробности, см. детали, например, здесь), напротив, приводит к расплыванию волны. Поскольку эти механизмы деформируют волну в противоположных направлениях, при определенных условиях они могут компенсировать друг друга - и тогда возникает волна Рассела или, иными словами, солитон (рисунок слева).
Оказывается, что скорость и ширина солитона связаны с его высотой A: чем выше солитон, тем он yже и тем быстрее движется, что вполне соответствует результатам экспериментов Рассела.
Уравнение КдФ имеет и многосолитонные решения; на рисунке справа видно, как быстрый солитон проходит через медленный и обгоняет его. Обратите внимание: высоты и скорости солитонов различаются в 2 раза, а вот ширина высокого в

меньше.
Интересны судьбы голландских математиков. Кортевег прожил долгую жизнь, успешно преподавал, руководил диссертантами, работал в различных областях математики, исследовал творчество Гюйгенса, в течение 60 (!) лет был членом Королевской Нидерландской академии искусств и наук и в течение 75 (!!!) лет членом Голландского математического общества. И всё-таки в первую очередь остался в истории, если так можно сказать, буквой К в уравнении КдФ.
Биография де Фриза оказалась совсем иной. В одной книге я видел утверждение о том, что неизвестна не только его последующая работа, но даже дата смерти. Это, конечно, не так, но три статьи, написанные совместно с руководителем, так и оказались единственным его вкладом в науку. Защитив диссертацию, он обратился к преподаванию в ремесленном училище, чем и занимался без малого сорок лет. Вот почему я и вспомнил в преамбуле цвейговского "Гения одной ночи"... Зато де Фриз стал отцом пятерых детей!*)
Как и Рассел, Кортевег и де Фриз опередили свое время. В конце XIX века их уравнение было не более чем красивой задачей, не имеющей практического применения. Возрождение интереса к этой проблеме наступило только в середине шестидесятых годов, когда появились работыНормана Забуски и Мартина Крускала. В мои планы не входит рассказывать сегодня о многочисленных явлениях и процессах солитонного типа - почитайте замечательную книгу Александра Филиппова "Многоликий солитон" (разве что для привлечения интереса замечу, что к солитонам относятся такие всем известные явления, как смерчи, цунами и прославленный Айвазовским "девятый вал"). Вот только чтобы оправдать ссылку в предисловии на Марка Твена вспомню курьёзную историю: Забуски и Крускал сперва хотели назвать уединенную волну, ведущую себя подобно частице, "солитроном" ("соло" - один, "трон" - по аналогии с электроном, нейтроном и т.п.), но обнаружилась фирма с таким названием, которая заявила свои права на это имя. Что ж - в науке появился термин "солитон", а фирма, упустившая халявную рекламу, в конце концов обанкротилась.
***
А началось всё с баржи на конной тяге и всадника, сопровождавшего ее вдоль Юнион Канала сто семьдесят пять лет назад. Что ж, с юбилеем тебя, солитон!
P.S. Господа ученые, не придирайтесь к упрощенному изложению! Оно так и задумано...
*) Биографии и портреты Рассела, Кортевега и де Фриза взяты с этого замечательного сайта по истории математики. Картинка, иллюстрирующая нелинейность - из книги Л.К.Мартинсона и Ю.И.Малова Дифференциальные уравнения математической физики.