Маркус Гард. Сеточная система вёрстки.
Оригинал взят у totsamiyshigaev в Маркус Гард. Сеточная система вёрстки.
Маркус Гард - шведский типограф-дизайнер-сеточник-публицист со всеми логичными вытекающими. С ними вы сможете познакомиться во вкусном портфолио обычного профи с многолетним стажем.
А ещё он как-то написал такую статью, которой мне вот не хватало. «Сеточная система вёрстки» называется. Такую статью, в которой всё - от и до, и даже история: сколько тут отступить, почему кегль такой, а зачем интерлиньяж нестандартный вычислять, поля по каким пропорциям ставить, откуда это всё пошло. Меня, ленивого, такие статьи балуют.
Годами учиться - это барская забота, а мне бы как раз наоборот: прочитал статейку, оп - и уже Индизайн ворочаешь, только клавиатура хрустит. Вот и перевёл для себя, потому как нет лучшего способа поизучать тему.
От Маркуса, всем нам тащемта:
I am Happy you like my webpage on Gridsystems. Your article on your website is really good, much better and easier to understand then mine. I have nothing against you Publishing The work on your website as long as you give me credit for The gridsystem. It makes me Happy to know that people in Russia can Benefit from My work. Thank you for making that possible.
All the best ;) Yours sincerely Marcus Garde
BachGarde Design and Communication AB
Villagatan 10 S-114 32 STOCKHOLM SWEDEN
www.bachgarde.com
VAT NO SE5566270160
Ph: +46 70 518 22 91
info@bachgarde.com
Сеточная система вёрстки
Маркус Гард, типограф | Оригинал статьи
Пятиколонная Тора

На фотографии свиток Торы, купленный в Праге. Он выполнен на пергаменте и датирован девятнадцатым веком. Язык Торы древний, поэтому ошибка фотографа, щёлкнувшего его перевёрнутым, вполне извинительна. Заметила казус внимательная kilja, за что ей отдельная благодарность от всех нас.
Размер свитка - 786 на 560 миллиметров. Сетка основана на восьмимиллиметровом интерлиньяже, равномерно распределённым по высоте страницы. Текстовые колонки по 464 миллиметра высотой и содержат по 58 линий. Ширина колонок - 131 миллиметр с 26-миллиметровым интервалом. Нижние поля - 56, а верхние - 40 миллиметров.
Разделив эти поля под интерлиньяж, равных чисел не получим: 56 / 8 = 7 и 40 / 8 = 5. То есть поля нечётные (в прежнем варианте перевода было «не равные»; исправлено благодаря вниманию Дмитрия Большакова). Далее: в свитке 58 линий текста - число чётное. Внешние поля составляют половину от внутренних - они по тринадцать миллиметров.
Отступы на сторонах соединения частей свитка семимиллиметровые: их наложение друг на друга привело к тринадцати миллиметрам, когда один миллиметр съелся при соединении. Так и получились 26 миллиметров с обеих сторон. Благодаря этому поддерживаются одинаковые размеры колонок на протяжении всего свитка.
То, что Тора спроектирована по сетке, чей интерлиньяж равномерно разделён в пространстве листа, как равно и то, что между пятью колонками интервалы не только равны, но и позволяют оставлять их таковыми при соединении частей пергамента, является доказательством знакомства древнего дизайнера с правилами сеточного проектирования вёрстки. И пожалуй, при использовании чисел пропорций, здесь не обошлось без концепции следования Пятикнижию. Косвенно это подтверждается тем фактом, что христианские монахи всюду использовали тройку там, где евреи применили бы пятёрку. В том числе и при создании книг.
Триколонная Тора

Этот свиток тоже из девятнадцатого века. Его размеры - 646 миллиметров в ширину и 584 в высоту. Кстати, мы тут постоянно мельтешим миллиметрами с претензией на точность, однако надо делать скидку на возраст пергамента, усыхающего со временем. Хотя, самое ценное для нас - соотношения - всё же верны. Итак, данный свиток свёрстан тремя колонками с интервалами в 28 миллиметров и с восмимиллиметровым интерлиньяжем.
Левое и правое поля - по 14 миллиметров, что есть по половине от двадцати восьми. Высота колонки - 440 миллиметров, ширина - 187. Итого: 440 делим на 8 и получаем 55 текстовых линий.
Верхнее и нижнее поля по 64 и 80 миллиметров, соответственно. Поделим их: 64/8 = 8 и 80/8 = 10. Итак, числа чётные. А 55 линий - число нечётное. С точки зрения цифровой магии получается некрасивенько. Но здесь мы снова возвращаемся к истории и традиции.
Дело в том, что две тысячи лет назад никаких миллиметров не было. А вот восьмёрка, присутствующая интерлиньяжем в обоих свитках, была. Например, известен восьмичастный метод деления триангуляцией.
Кроме того, восьмёрка - одно из священных чисел в иудаизме. Например, это число праздника Брит Мила: прародитель евреев Исаак был обрезан на восьмой день своей жизни. Ещё есть восьмидневная Ханука, начинающаяся на двадцать пятый день Кислева. Потом Шмини Ацерет - восьмой завершающий день праздника Суккот. Всё это вполне может быть причиной постоянного присутствия восьмёрки при вёрстке свитков Торы.
Маркус Гард и сетки по расчётам
Как выяснил Маркус, в процессе подготовки к изданию своей книги «Путь вёрстки», его новый метод оказался близок к дизайну древних свиточных книг. Во время исследований, он обнаружил то, что дизайн тех свитков не просто разработан по-иному, чем делают это теперь. Он оказался более сложным, следующим большему числу условий.
Содержимое древних книг основывалось на чётко просчитанной сетке базовых линий. И даже корешковые отступы были пропорциональны полям под срез. Например, у Гутенберга отступы корешка составляют одну треть от внешних полей, а внутренние - половину от внешних. Область его вёрстки состоит из шести частей, а они, в свою очередь, поделены тоже на шесть. Это даёт тридцать шесть линий текста. А вот в первой книге первопечатника, каждый из этих шести модулей поделён на семь. Поэтому текстовых линий в ней сорок две.
Сегодня мы зачастую лукавим: просто выставляем начало базовых линий и далее позволяем тексту стекать вниз. Мы не всегда уточняем - как соотносятся друг к другу верхнее поле и обрез. В прежние времена без этого не обходились.
Благодаря Моабитскому Камню, про еврейское письмо сегодня нам известно следующее: оно возникло, как минимум, за 850 лет до рождения Христа, а Ханаатско-Феникийский алфавит состоял из двадцати двух согласных и при этом гласных не имел вовсе. Со временем, иврит перестал быть разговорным, но продолжает использоваться в священных писаниях.
Свиток Торы включает в себя 304805 букв или приблизительно 79000 слов, а его копирование занимает около двух тысяч часов работы софера. Но если хоть один символ написан неверно, то, по традиции, весь свиток лишается законной силы. Лучшим способом избежать ошибок остаётся копирование свитков один к одному. А это, в свою очередь, гарантирует: сегодня они выполняются в том же дизайне, что и две тысячи лет назад. Кстати, так же - на животном материале: на скреплённых кусках пергамента.
Классические структуры
Ян Чихольд (1902 - 1974) является автором трёх работ по книгоизданию, ставших классикой темы. Это «Новая вёрстка» 1927-го года, «Пропорции книги» 1955-го и «Облик книги». Последняя, по сути, является сборником его эссе, написанных в период между 1937-ым и 1975-ым годами. Этот сбоник - обсуждение всех факторов, влияющих на классический книжный проект. Ян много лет проработал в «Пингвин Букс», где, кроме прочего, заложил основы издания книг в мягкой обложке.
Чихольда заинтересовал один из методов Ван де Граафа. В своей книге «Новые расчёты проектирования» он приводит разметку, сравнимую с методом Розариво: страница поделена на девять двойными диагоналями и несколькими направляющими.

В результате применения метода, получаем соотношение полей «корешковое: верхнее: : внешнее: нижнее» как «2 : 3 : : 4 : 6», при соотношении сторон исходного поля «2 : 3». Чихольд высоко оценил метод, популяризировав его в двух последних книгах. Да так, что его стали называть «методом Чихольда». Кстати, есть и другая конструкция, позволяющая получить тот же результат:
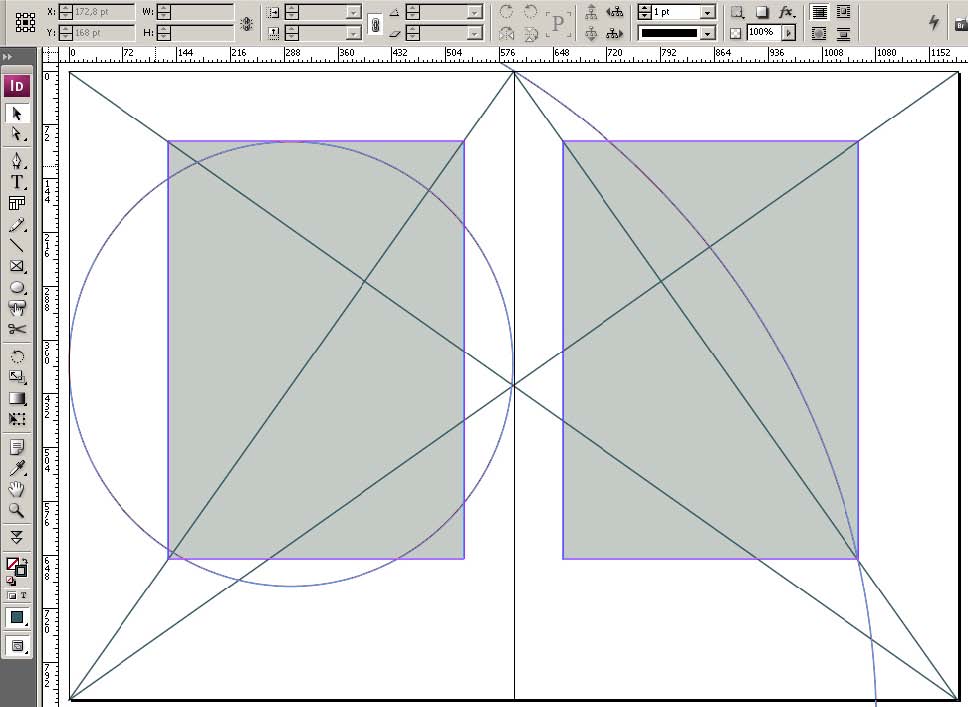
Рауль Марио Розариво (1903 - 1966) родился в Буэнос-Айресе. Типогрф, исследователь, дизайнер, поэт, художник, иллюстратор - более всего он известен работой по исследованию Библии Гутенберга. В своей «Божественной пропорции вёрстки» 1948-го года, Розариво описывает - сколько классических книг было разработано по модулю, в итоге названного им «Модуль 1.5». Изучив некоторые из первых книг, вы заметите: все их сетки основаны на тройке. Есть два способа такой разметки. Первый - это уже описанная версия диагоналей Розариво. Метод можно отыскать и в «Философии дизайна» Германа Цапфа, применяется он в книгах Чихольда и Ганса Рудольфа Босшарда. Второй - тоже метод Розариво - метод сетки «девять на девять»:

Основываясь на анализе старых книг, Маркус создал пошаговое руководство для сетки, регулируемой пропорциями обреза листа. Оно вошло в его книгу «Путь вёрстки», выпущенную в 2007-ом году.
Помогал ему Аврам Жоржес - его бывший студент, известный своей работой «Форма и бесформие». Он сделал программу - калькулятор сетки для «Дизайнерс Букшоп». Про-версия вроде бы устанавливается в Индизайн, как на Mac, так и на Windows, а базовый вариант представляет собой отдельное приложение и стоит под сорок долларов.
Такой калькулятор - прекрасное подспорье начинающим, ещё не вполне изучившим сеточную систему, но уже понимающим её необходимость - тем, кто стремится создавать сетки быстро и без усилий. На сайте Букшопа есть полезное и недлинное видео, описывающее, как сам калькулятор, так и многие из методов, рассмотренных в этой статье.
Базовый метод расчёта сеток для Adobe Indesign
Условные обозначения:
Формула создания сетки, пропорциональной листу:
Сетка для бумаги определённого формата
В предыдущем примере имелась свобода выбора формата бумаги, а условием было лишь деление на три. Теперь мы увидим - насколько полезен следующий метод, позволяющий распределить сетку на всё поле листа любого формата и выравнивать картинки по верхнему краю строчных букв. Пробовать будем на А4.
Переведём миллиметры в пункты:
Определимся с пропорциями бумаги:
Сетка базовых линий:

Направляющие для выравнивания изображений
Выберем шрифт и назначим ему девятый кегль.
В итоге - имеем те направляющие, по которым будем выравнивать изображения. На картинке это линия 2. Теперь вставленное изображение будет смотреться единым блоком с боковым текстом. И всё благодаря тому, что оно выровнено по верхним границам строчных букв.

Работаем с вертикальными направляющими
У них будет свой интервал, а высчитываем его так:
Индизайн не был бы Индизайном без автоматизации всей этой рутины. Так и есть: сетку можно создать вводом данных в Settings > Grids. Здесь просто расставляем полученные числа: leading - 10,934 и vertical line - 7,731. Намного быстрее, чем «Step and repeat».

Блоки строк и колонок
Набросаем четыреколонную вёрстку текста. Надо выяснить - какие внешние и внутренние поля подходят для неё, а так же - какое будет межколонное пространство. Это несложно: мы это всё просто измерим после размещения и запишем в Layout > Margins and columns.
Остаётся ровно расположить наши текстовые колонки относительно друг друга, а весь их блок - максимально по середине, в чём нам наглядно поможет сетка. В итоге, слева у нас остаются пять ячеек, а справа шесть. Блок колонок почти посередине и чуть сдвинут к корешку, что нормально.
При этом мы выравниваем их точно по вертикальным направляюшим. Скажем - на расстоянии двух ячеек: 7,731 × 2 ≈ 15,4617 pt. Запишем это число в Индизайн как Column spacing, а суммы пустых ячеек слева и справа - как левое и правое поля, соответственно.

Размещение горизонтальных блоков
Выбираем - сколько блочных рядов под картинки нас устроит. В данном случае их пять. Раскидаем их по листу так же, как раскидывали колонки - пока их расположение не закрепится во взгляде и пока между ними не будет равных интервалов. Теперь измеряем оставшиеся внутренние и внешние поля, а так же горизонтальные интервалы между блоками. Осталось записать их в Layout > Margins and spacing.
Убедитесь в том, что верхние края блоков соответствуют высоте «f», а нижние края выровнены по базовым линиям.
Можно создать блоки строк и по направляющим. Сделаем пять напрвляющих: Layout > Make guidelines.
Для определения интервала между ними, сложим интерлиньяж с разницей между ним и высотой нашей выручалки - строчной «f»: 10,934 + (10,934 − 6,148) = 15,2 pt.
(* Ранее была неточность «умножим интерлиньяж на разницу». Исправлено благодаря внимательности hardtmuth *)
При этом проверьте то, чтобы направляющие отсчитывались от полей, отметив соответствующую опцию в диалоговм окне.
Теперь мы получили добротно сделанную и функциональную сетку. Её цель в том, чтобы все элементы вёрстки нашли свои естественные места, не вызывая диссонанса у зрителя. В этом нет противоречия со свободой творчества: ведь строгая сетка - это его базис. На нём уже можно развернуться и показать свои способности художника-верстальщика. Иначе, какой смысл в работе, где элементы толкают друг друга и вводят зрителя в сомнение о своей уместности?

Определение полей в классической сетке строится на соотношении - «2 : 3 : : 4 : 6». Но не всегда можно держаться этого правила. Ведь есть ещё и журналы, где большие поля - это потеря драгоценного места. Казалось бы, здесь неизбежна и потеря гармонии. Но всегда выручит грамотный расчёт, основанный на соотношении колонок, расстояний между ними и размером печатной области.
При помощи описанного метода можно создать любые сетки для дизайна. Ограничений нет:


Сетка, привязанная к кеглю
Эта сетка основана на одном из методов измерения символов - на пригонке по «EM space». Другими словами - на ширине буквы «М», самой широкой из букв.
Начнём создавать сетку, основываясь на уже описанных модулях. Текст используем кеглем в 10 pt. При этом, ширина страницы - 150 миллиметров или 425,197 pt.
Считаем:
Получаем новый размер текста: 10,124. Переходим в Preferences > Grids: Horisontal: 10,124 pt.
На сколько поделить (Subdivisions) каждую из EM-ячеек - можно решить по потребностям. Например, автор предпочитает делить на четыре, так как работает с тонкими пробелами в ¼ EM. Итак, выставляем - Subdivisions: 4.
У вертикалей можно оставить отступы, созданные в предыдущих примерах. Или можно изменить их, подогнав под новый кегль.
Теперь мы получили такую сетку, которая наиболее точно позиционирует горизонтальное расположение текста. Стало ещё проще определиться с печатной областью, основанной на ширине EM-квадрата конкретного кегля. Только не забудьте изменить размер текста в стиле параграфа (Paragraph Style).

Маркус Гард - шведский типограф-дизайнер-сеточник-публицист со всеми логичными вытекающими. С ними вы сможете познакомиться во вкусном портфолио обычного профи с многолетним стажем.
А ещё он как-то написал такую статью, которой мне вот не хватало. «Сеточная система вёрстки» называется. Такую статью, в которой всё - от и до, и даже история: сколько тут отступить, почему кегль такой, а зачем интерлиньяж нестандартный вычислять, поля по каким пропорциям ставить, откуда это всё пошло. Меня, ленивого, такие статьи балуют.
Годами учиться - это барская забота, а мне бы как раз наоборот: прочитал статейку, оп - и уже Индизайн ворочаешь, только клавиатура хрустит. Вот и перевёл для себя, потому как нет лучшего способа поизучать тему.
От Маркуса, всем нам тащемта:
I am Happy you like my webpage on Gridsystems. Your article on your website is really good, much better and easier to understand then mine. I have nothing against you Publishing The work on your website as long as you give me credit for The gridsystem. It makes me Happy to know that people in Russia can Benefit from My work. Thank you for making that possible.
All the best ;) Yours sincerely Marcus Garde
BachGarde Design and Communication AB
Villagatan 10 S-114 32 STOCKHOLM SWEDEN
www.bachgarde.com
VAT NO SE5566270160
Ph: +46 70 518 22 91
info@bachgarde.com
Сеточная система вёрстки
Маркус Гард, типограф | Оригинал статьи
- Пятиколонная Тора
- Триколонная Тора
- Маркус Гард и сетки по расчётам
- Классические структуры
- Базовый метод расчёта сеток для Adobe Indesign
- Сетка для бумаги определённого формата
- Направляющие для выравнивания изображений
- Работаем с вертикальными направляющими
- Блоки строк и колонок
- Размещение горизонтальных блоков
- Сетка, привязанная к кеглю
Пятиколонная Тора

На фотографии свиток Торы, купленный в Праге. Он выполнен на пергаменте и датирован девятнадцатым веком. Язык Торы древний, поэтому ошибка фотографа, щёлкнувшего его перевёрнутым, вполне извинительна. Заметила казус внимательная kilja, за что ей отдельная благодарность от всех нас.
Размер свитка - 786 на 560 миллиметров. Сетка основана на восьмимиллиметровом интерлиньяже, равномерно распределённым по высоте страницы. Текстовые колонки по 464 миллиметра высотой и содержат по 58 линий. Ширина колонок - 131 миллиметр с 26-миллиметровым интервалом. Нижние поля - 56, а верхние - 40 миллиметров.
Разделив эти поля под интерлиньяж, равных чисел не получим: 56 / 8 = 7 и 40 / 8 = 5. То есть поля нечётные (в прежнем варианте перевода было «не равные»; исправлено благодаря вниманию Дмитрия Большакова). Далее: в свитке 58 линий текста - число чётное. Внешние поля составляют половину от внутренних - они по тринадцать миллиметров.
Отступы на сторонах соединения частей свитка семимиллиметровые: их наложение друг на друга привело к тринадцати миллиметрам, когда один миллиметр съелся при соединении. Так и получились 26 миллиметров с обеих сторон. Благодаря этому поддерживаются одинаковые размеры колонок на протяжении всего свитка.
То, что Тора спроектирована по сетке, чей интерлиньяж равномерно разделён в пространстве листа, как равно и то, что между пятью колонками интервалы не только равны, но и позволяют оставлять их таковыми при соединении частей пергамента, является доказательством знакомства древнего дизайнера с правилами сеточного проектирования вёрстки. И пожалуй, при использовании чисел пропорций, здесь не обошлось без концепции следования Пятикнижию. Косвенно это подтверждается тем фактом, что христианские монахи всюду использовали тройку там, где евреи применили бы пятёрку. В том числе и при создании книг.
Триколонная Тора

Этот свиток тоже из девятнадцатого века. Его размеры - 646 миллиметров в ширину и 584 в высоту. Кстати, мы тут постоянно мельтешим миллиметрами с претензией на точность, однако надо делать скидку на возраст пергамента, усыхающего со временем. Хотя, самое ценное для нас - соотношения - всё же верны. Итак, данный свиток свёрстан тремя колонками с интервалами в 28 миллиметров и с восмимиллиметровым интерлиньяжем.
Левое и правое поля - по 14 миллиметров, что есть по половине от двадцати восьми. Высота колонки - 440 миллиметров, ширина - 187. Итого: 440 делим на 8 и получаем 55 текстовых линий.
Верхнее и нижнее поля по 64 и 80 миллиметров, соответственно. Поделим их: 64/8 = 8 и 80/8 = 10. Итак, числа чётные. А 55 линий - число нечётное. С точки зрения цифровой магии получается некрасивенько. Но здесь мы снова возвращаемся к истории и традиции.
Дело в том, что две тысячи лет назад никаких миллиметров не было. А вот восьмёрка, присутствующая интерлиньяжем в обоих свитках, была. Например, известен восьмичастный метод деления триангуляцией.
Кроме того, восьмёрка - одно из священных чисел в иудаизме. Например, это число праздника Брит Мила: прародитель евреев Исаак был обрезан на восьмой день своей жизни. Ещё есть восьмидневная Ханука, начинающаяся на двадцать пятый день Кислева. Потом Шмини Ацерет - восьмой завершающий день праздника Суккот. Всё это вполне может быть причиной постоянного присутствия восьмёрки при вёрстке свитков Торы.
Маркус Гард и сетки по расчётам
Как выяснил Маркус, в процессе подготовки к изданию своей книги «Путь вёрстки», его новый метод оказался близок к дизайну древних свиточных книг. Во время исследований, он обнаружил то, что дизайн тех свитков не просто разработан по-иному, чем делают это теперь. Он оказался более сложным, следующим большему числу условий.
Содержимое древних книг основывалось на чётко просчитанной сетке базовых линий. И даже корешковые отступы были пропорциональны полям под срез. Например, у Гутенберга отступы корешка составляют одну треть от внешних полей, а внутренние - половину от внешних. Область его вёрстки состоит из шести частей, а они, в свою очередь, поделены тоже на шесть. Это даёт тридцать шесть линий текста. А вот в первой книге первопечатника, каждый из этих шести модулей поделён на семь. Поэтому текстовых линий в ней сорок две.
Сегодня мы зачастую лукавим: просто выставляем начало базовых линий и далее позволяем тексту стекать вниз. Мы не всегда уточняем - как соотносятся друг к другу верхнее поле и обрез. В прежние времена без этого не обходились.
Благодаря Моабитскому Камню, про еврейское письмо сегодня нам известно следующее: оно возникло, как минимум, за 850 лет до рождения Христа, а Ханаатско-Феникийский алфавит состоял из двадцати двух согласных и при этом гласных не имел вовсе. Со временем, иврит перестал быть разговорным, но продолжает использоваться в священных писаниях.
Свиток Торы включает в себя 304805 букв или приблизительно 79000 слов, а его копирование занимает около двух тысяч часов работы софера. Но если хоть один символ написан неверно, то, по традиции, весь свиток лишается законной силы. Лучшим способом избежать ошибок остаётся копирование свитков один к одному. А это, в свою очередь, гарантирует: сегодня они выполняются в том же дизайне, что и две тысячи лет назад. Кстати, так же - на животном материале: на скреплённых кусках пергамента.
Классические структуры
Ян Чихольд (1902 - 1974) является автором трёх работ по книгоизданию, ставших классикой темы. Это «Новая вёрстка» 1927-го года, «Пропорции книги» 1955-го и «Облик книги». Последняя, по сути, является сборником его эссе, написанных в период между 1937-ым и 1975-ым годами. Этот сбоник - обсуждение всех факторов, влияющих на классический книжный проект. Ян много лет проработал в «Пингвин Букс», где, кроме прочего, заложил основы издания книг в мягкой обложке.
Чихольда заинтересовал один из методов Ван де Граафа. В своей книге «Новые расчёты проектирования» он приводит разметку, сравнимую с методом Розариво: страница поделена на девять двойными диагоналями и несколькими направляющими.

В результате применения метода, получаем соотношение полей «корешковое: верхнее: : внешнее: нижнее» как «2 : 3 : : 4 : 6», при соотношении сторон исходного поля «2 : 3». Чихольд высоко оценил метод, популяризировав его в двух последних книгах. Да так, что его стали называть «методом Чихольда». Кстати, есть и другая конструкция, позволяющая получить тот же результат:

Рауль Марио Розариво (1903 - 1966) родился в Буэнос-Айресе. Типогрф, исследователь, дизайнер, поэт, художник, иллюстратор - более всего он известен работой по исследованию Библии Гутенберга. В своей «Божественной пропорции вёрстки» 1948-го года, Розариво описывает - сколько классических книг было разработано по модулю, в итоге названного им «Модуль 1.5». Изучив некоторые из первых книг, вы заметите: все их сетки основаны на тройке. Есть два способа такой разметки. Первый - это уже описанная версия диагоналей Розариво. Метод можно отыскать и в «Философии дизайна» Германа Цапфа, применяется он в книгах Чихольда и Ганса Рудольфа Босшарда. Второй - тоже метод Розариво - метод сетки «девять на девять»:

Основываясь на анализе старых книг, Маркус создал пошаговое руководство для сетки, регулируемой пропорциями обреза листа. Оно вошло в его книгу «Путь вёрстки», выпущенную в 2007-ом году.
Помогал ему Аврам Жоржес - его бывший студент, известный своей работой «Форма и бесформие». Он сделал программу - калькулятор сетки для «Дизайнерс Букшоп». Про-версия вроде бы устанавливается в Индизайн, как на Mac, так и на Windows, а базовый вариант представляет собой отдельное приложение и стоит под сорок долларов.
Такой калькулятор - прекрасное подспорье начинающим, ещё не вполне изучившим сеточную систему, но уже понимающим её необходимость - тем, кто стремится создавать сетки быстро и без усилий. На сайте Букшопа есть полезное и недлинное видео, описывающее, как сам калькулятор, так и многие из методов, рассмотренных в этой статье.
Базовый метод расчёта сеток для Adobe Indesign
Условные обозначения:
- Оригинальный интерлиньяж = OL
- Ширина листа = W
- Высота листа = H
- Новый интерлиньяж = L
- Соотношение размеров листа «Ширина: Высота» = W: H
- Соотношение размеров листа «Высота: Ширина» = H: W
- Новая ширина интерлиньяжа = LW
- Так же как = : :
- Соотношение = :
Формула создания сетки, пропорциональной листу:
- H / OL = Y ≈ X (округляем «Y» до ближайшего целого)
- H / X = L
- L (W / H) = LW
- L : LW : : H : W
Сетка для бумаги определённого формата
В предыдущем примере имелась свобода выбора формата бумаги, а условием было лишь деление на три. Теперь мы увидим - насколько полезен следующий метод, позволяющий распределить сетку на всё поле листа любого формата и выравнивать картинки по верхнему краю строчных букв. Пробовать будем на А4.
Переведём миллиметры в пункты:
- 297 мм ≈ 841,89 pt
- 210 мм ≈ 595,276 pt
- Кегль = 9 pt
- Интерлиньяж = 11 pt
Определимся с пропорциями бумаги:
- 841,89 / 595,276 ≈ 1,414
- 595,276 / 841,89 ≈ 0,7070
Сетка базовых линий:
- Берём такой интерлиньяж, который обычен для данного кегля - 11pt. Соответственно этому, делим высоту бумаги: 841,89 / 11 = 76,5354 ≈ 77.
- Осталось получить точный интерлиньяж: 841.89 / 77 ≈ 10.934 pt.
- Запускаем наш Adobe InDesign и создаём документ в формате A4. Теперь применяем расчёты, вводя: Settings > Grids > Start - Increase every: 10,934 pt. В результате имеем базовые линии, равномерно распределённые по всей высоте листа:

Направляющие для выравнивания изображений
Выберем шрифт и назначим ему девятый кегль.
- Теперь напечатаем «f» и выведем её контур: Type > Outlines.
- Выделив символ чёрной стрелкой, в палитре Transform увидим её высоту (H). Например, если был выбран Times, то это будет 6,148 pt.
- Берём эту высоту и вычитаем её из интерлиньяжа: 10,934 − 6,148 = 4,786 pt.
- Хватаем новую направляющую из верхней линейки (Ctrl+R, если не отображаются), и ставим на границу верхнего поля. Затем сдвигаем её на 4,786 pt вниз, через команду контекстного меню «Moove».
- Ну а теперь надо всё это повторить 76 раз. Автоматизируем процесс: Edit > Step and Repeat, вводим «76» как число базовых линий минус одна. Назначаем им уже знакомый интервал в 10,934 pt.
В итоге - имеем те направляющие, по которым будем выравнивать изображения. На картинке это линия 2. Теперь вставленное изображение будет смотреться единым блоком с боковым текстом. И всё благодаря тому, что оно выровнено по верхним границам строчных букв.

Работаем с вертикальными направляющими
У них будет свой интервал, а высчитываем его так:
- 841,89 / 77 - это знакомая формула получения интерлиньяжа.
- Её результат мы должны умножить на результат деления ширины на высоту - 595,276 / 841,89.
- Итак, вот наш новый интервал для вертикальных направляющих: (841,89 / 77) × (595,276 / 841,89) ≈ 7,731.
- Размножим линии через «Step and repeat». Сначала включим их отображение: Show > Show rulers. Перетащим направляющую с левой линейки на документ и выделим её. Если не получается, то разблокируем направляющие: Show > Unlock guideline.
- Выделив, переходим в Edit > Step и вводим ранее полученное число линий. У нас получились 77 штук с интервалом в 7,731 pt.
Индизайн не был бы Индизайном без автоматизации всей этой рутины. Так и есть: сетку можно создать вводом данных в Settings > Grids. Здесь просто расставляем полученные числа: leading - 10,934 и vertical line - 7,731. Намного быстрее, чем «Step and repeat».

Блоки строк и колонок
Набросаем четыреколонную вёрстку текста. Надо выяснить - какие внешние и внутренние поля подходят для неё, а так же - какое будет межколонное пространство. Это несложно: мы это всё просто измерим после размещения и запишем в Layout > Margins and columns.
Остаётся ровно расположить наши текстовые колонки относительно друг друга, а весь их блок - максимально по середине, в чём нам наглядно поможет сетка. В итоге, слева у нас остаются пять ячеек, а справа шесть. Блок колонок почти посередине и чуть сдвинут к корешку, что нормально.
При этом мы выравниваем их точно по вертикальным направляюшим. Скажем - на расстоянии двух ячеек: 7,731 × 2 ≈ 15,4617 pt. Запишем это число в Индизайн как Column spacing, а суммы пустых ячеек слева и справа - как левое и правое поля, соответственно.

Размещение горизонтальных блоков
Выбираем - сколько блочных рядов под картинки нас устроит. В данном случае их пять. Раскидаем их по листу так же, как раскидывали колонки - пока их расположение не закрепится во взгляде и пока между ними не будет равных интервалов. Теперь измеряем оставшиеся внутренние и внешние поля, а так же горизонтальные интервалы между блоками. Осталось записать их в Layout > Margins and spacing.
Убедитесь в том, что верхние края блоков соответствуют высоте «f», а нижние края выровнены по базовым линиям.
Можно создать блоки строк и по направляющим. Сделаем пять напрвляющих: Layout > Make guidelines.
Для определения интервала между ними, сложим интерлиньяж с разницей между ним и высотой нашей выручалки - строчной «f»: 10,934 + (10,934 − 6,148) = 15,2 pt.
(* Ранее была неточность «умножим интерлиньяж на разницу». Исправлено благодаря внимательности hardtmuth *)
При этом проверьте то, чтобы направляющие отсчитывались от полей, отметив соответствующую опцию в диалоговм окне.
Теперь мы получили добротно сделанную и функциональную сетку. Её цель в том, чтобы все элементы вёрстки нашли свои естественные места, не вызывая диссонанса у зрителя. В этом нет противоречия со свободой творчества: ведь строгая сетка - это его базис. На нём уже можно развернуться и показать свои способности художника-верстальщика. Иначе, какой смысл в работе, где элементы толкают друг друга и вводят зрителя в сомнение о своей уместности?

Определение полей в классической сетке строится на соотношении - «2 : 3 : : 4 : 6». Но не всегда можно держаться этого правила. Ведь есть ещё и журналы, где большие поля - это потеря драгоценного места. Казалось бы, здесь неизбежна и потеря гармонии. Но всегда выручит грамотный расчёт, основанный на соотношении колонок, расстояний между ними и размером печатной области.
При помощи описанного метода можно создать любые сетки для дизайна. Ограничений нет:


Сетка, привязанная к кеглю
Эта сетка основана на одном из методов измерения символов - на пригонке по «EM space». Другими словами - на ширине буквы «М», самой широкой из букв.
Начнём создавать сетку, основываясь на уже описанных модулях. Текст используем кеглем в 10 pt. При этом, ширина страницы - 150 миллиметров или 425,197 pt.
Считаем:
- 425,197 / 10 = 42,5197 ≈ 42 (или 43, решаейте сами)
- 425,197 / 43 ≈ 10,123738095238095
Получаем новый размер текста: 10,124. Переходим в Preferences > Grids: Horisontal: 10,124 pt.
На сколько поделить (Subdivisions) каждую из EM-ячеек - можно решить по потребностям. Например, автор предпочитает делить на четыре, так как работает с тонкими пробелами в ¼ EM. Итак, выставляем - Subdivisions: 4.
У вертикалей можно оставить отступы, созданные в предыдущих примерах. Или можно изменить их, подогнав под новый кегль.
Теперь мы получили такую сетку, которая наиболее точно позиционирует горизонтальное расположение текста. Стало ещё проще определиться с печатной областью, основанной на ширине EM-квадрата конкретного кегля. Только не забудьте изменить размер текста в стиле параграфа (Paragraph Style).
