time
Посмотрев осенью Interstellar, я вспомнил, что давно хотел поближе познакомиться с general relativity, а то я кроме нескольких общих фраз о ней и не знал ничего почти. Ну и в общем увяз на всю зиму, очень тема увлекательная оказалась, торкает похлеще зависимых типов. Как тогда метко сказал levgem, "физика штырит сильнее химии". Популярные книжки и передачи крайне поверхностны и не отвечают на множество вопросов, пришлось нырнуть в атласы, карты, metric tensor, Christoffel symbols, covariant derivatives, Riemann curvature tensor, Ricci tensor и scalar, stress-energy tensor, Killing vectors, Schwarzschild solution, Kerr solution, вот это все. После сотен страниц литературы и десятков часов лекций начали появлятся зачатки понимания. Кое-какими находками и хочу поделиться.
Один вопрос меня живо интересовал, в частности. Вот говорится, что при приближении к черной дыре "время замедляется", и чем ближе к горизонту событий, тем сильнее. Для внешнего наблюдателя падающий в черную дыру корабль по мере приближения к горизонту будет двигаться все медленнее и медленнее и так никогда горизонта не достигнет. Т.е. не просто очень долго будет падать, а вообще _никогда_ не долетит до ЧД. (Будем считать черную дыру постоянной и забьем пока на эффект их испарения, это уже кванты.) А с точки зрения падающего в черную дыру, он туда таки упадет довольно быстро, пересечет горизонт событий и продолжит движение внутрь до самой сингулярности в центре. Но как это возможно, если он подлетает к ЧД бесконечно долго, получается эдакое "никогда, а потом..."? Оказалось, что этот кажущийся парадокс был вызван моим непониманием течения времени, и время - это не прямое шоссе, по которому можно двигаться быстрее или медленнее, а более правильно думать об измеренном времени как о длине пути, и пути могут быть самые разные в разные стороны. Как можно в из одной точки в другую добраться разными путями с разными длинами, и как можно проехать одинаковые расстояния, но оказаться совсем в разных точках, так и со временем, оно зависит от траектории, и одинаковые показания часов еще не означают одновременности событий, в частности.
В одной публичной лекции про черные дыры Susskind упомянул, что эта ситуация с разницей времен падающего в ЧД и внешнего наблюдателя аналогична случаю, где нет никакой черной дыры, пустое плоское пространство, и просто один из наблюдателей равномерно ускоряется и улетает от другого. И действительно ведь, один из вариантов принципа эквивалентности, из которого вся эта теория выросла, гласит, что нахождение в гравитационном поле эквивалентно соответствующему ускорению в пространстве без оного. Двигается ли наша ракета в космосе с ускорением g или стоит на Земле, изнутри определить крайне сложно (на самом деле небольшая разница будет - приливные силы - но если представить однородное гравитационное поле, то она исчезнет). Так вот, упомянутый вариант с ускоряющимся наблюдателем в пустом пространстве известен под именем Rindler coordinates. Что интересно, для его описания достаточно special relativity. Суть такова™. Пусть у нас есть два космонавта, Алиса и Боб. Изначально они вместе висят в пустом пространстве в одной точке. Ровно в 10:00 Боб включает двигатель на своей ракете и начинает удаляться с ускорением 83.3 км/с2 (будем считать, что он опытный штангист и легко выдержит такую перегрузку :) ). Алиса остается на месте. Боб сохраняет постоянное ускорение в его собственной системе координат, т.е. испытывает одну и ту же перегрузку. В системе координат Алисы Боб летит все быстрее и быстрее, и согласно специальной теории относительности время у него тикает все медленее, поэтому его ускорение в системе координат Алисы постепенно уменьшается и по мере приближения скорости к скорости света она растет все медленнее, так никогда и не доходя до скорости света. Поэтому в системе координат Алисы траектория Боба выглядит не как парабола, а как гипербола (X2 - T2 = const). Спустя час, в 11:00 Алиса в точке А прикидывает, сколько времени сейчас показывают часы Боба, который сейчас в точке В. Они уже несколько замедлились, и в этой точке его истории показывают только 10:52. Теперь если мы посмотрим на Боба в точке В, то стоит вспомнить, что дело происходит в пространстве Минковского, и плоскость одновременных ему событий, точки, вектора к которым от него перпендикулярны вектору его движения в пространстве-времени, поворачивается не в ту же сторону, куда вектор скорости, а навстречу ему (в пространстве Минковского вектору (dt, dx) перпендикулярен вектор (dx, dt), т.к. в скалярном произведении у одного из компонентов стоит минус). В результате с т.з. Боба в В ему одновременен момент в истории Алисы, где она в точке С. Там на ее часах только 10:42.
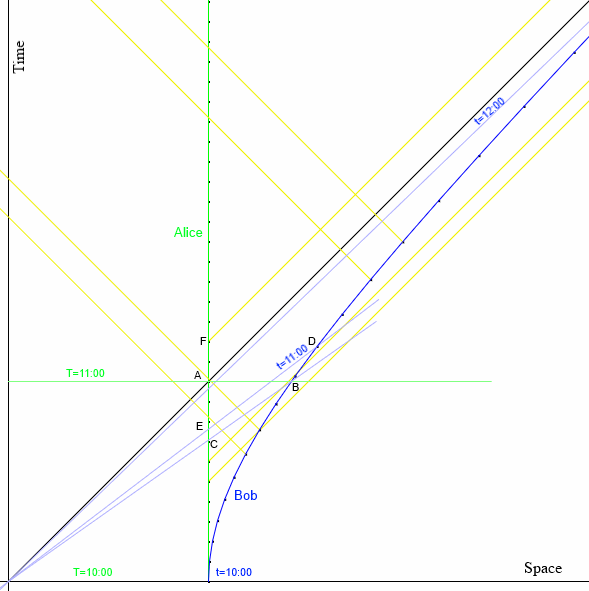
Чем примечательна такая гипербола, в каждой ее точке "перпендикуляр" (в минковском смысле) к касательной проходит через начало координат.
Когда на часах Боба настает 11:00 (точка D), для него одновременен момент Алисы в точке Е, где ее часы показывают 10:45. Когда на часах Боба 12:00, на часах Алисы с его т.з. 10:57. В системе координат Боба часы Алисы тикают все медленнее и медленнее и никогда они не достигнут отметки 11:00. Траектория Боба уходит вверх и вправо в бесконечность, стремясь к диагональной линии, но никогда ее не достигая. Его плоскости одновременности проходят от него к началу координат и тоже никогда не достигнут диагонали T=X. Эта диагональ - горизонт событий для Боба. Любое событие за ним, например F, никогда не настанет для Боба, и свет от него никогда к нему не придет. На ровном месте в пустом пространстве мы получили горизонт событий, ведущий себя ровно как горизонт черной дыры. Можно представить, что Боб на самом деле стоит на месте в постоянном гравитационном поле, а Алиса свободно падает в сторону горизонта (у нее всю дорогу невесомость, кстати) и дальше. Во многом эта ситуация действительно совпадает со сценарием черной дыры, для черной дыры есть точно такой же график с гиперболами и плоским горизонтом, просто координаты чуть иначе определяются (Kruskal coordinates). Тут становится видно, как сочетаются утверждения, что свободно падающая Алиса горизонт вообще не замечает, проходит его спокойно в 11:00 и для нее ничего не происходит, в то время как для "внешнего наблюдателя" Боба она замедляется и практически замирает, так никогда и не доходя до горизонта. Еще можно посмотреть на лучи света, испускаемые ими (желтенькие на картинке). Отметки на траекториях Алисы и Боба расставлены с равными интервалами по их часам. Видно, что как Боб видит Алисино время замедленным, так и Алиса видит Боба замедленным. В интернетах порой можно встретить описания падения в черную дыру, где говорят, что из-за "замедления времени" при приближении к оной можно увидеть, как вселенная вокруг ускоряет свой ход. Так вот, это неправда, вселенная вокруг будет выглядеть также замедленной (но не очень сильно, т.к. долго полюбоваться замедлением не выйдет, сингулярность тебя встретит за весьма ограниченное время).
Вот если взять двух наблюдателей, зависших над черной дырой, или что то же самое двух ускоряющихся в пустом пространстве Боба и Чарли, то там уже действительно Чарли, который "выше" (= у него ускорение меньше) будет видеть Боба замедленным, а Боб будет видеть Чарли ускоренным. Это как раз похоже на то, что в кино было.
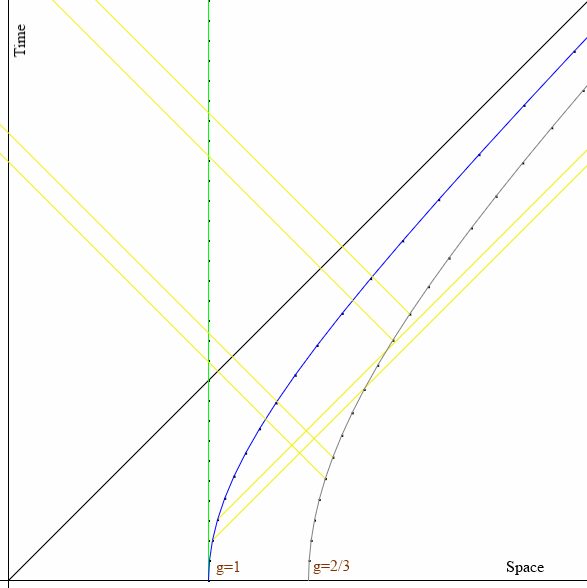
В случае Rindler coordinates, если ускорения Боба и Чарли связаны с их начальным положением как g = c2/X, то в их собственных системах координат они будут оба неподвижны относительно друг друга. Это как раз аналог двух зависших на разных высотах над массивным телом наблюдателей.
Еще у меня есть картинка, как в системе координат Боба будет выглядеть "падение" Алисы.
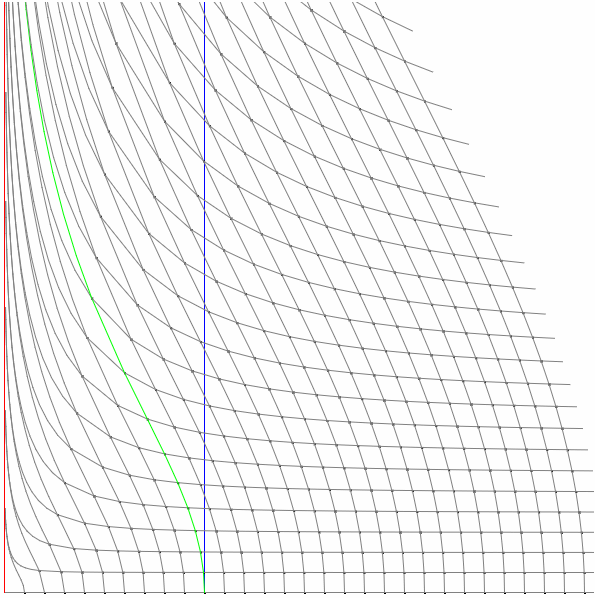
Она сперва будет удаляться с ускорением, потом начнет замедляться и будет все медленнее и медленнее приближаться к горизонту, обозначенному тут красной линией. Что занятно, и уже понятно из вышеописанного, на этом графике, даже если продлить его вверх в бесконечность, отражен лишь первый час истории Алисы, а ее достижение горизонта и дальнейшая судьба в этих координатах отстутствует вовсе. Серые линии показывают, во что превратилась регулярная сетка координат Алисы. Они так ловко загибаются, что как ни двигайся по ним в пространстве и времени, на красную линию горизонта не попадешь. Этот момент, что в одних координатах у нас может быть принципиально больше разных мест и событий, чем в других, лежит в основе далеко идущих предсказаний о wormholes. Вот на графиках выше у нас есть обычное пространство-время с обеих сторон от горизонта (который ничем особенным и не является для Алисы и многих других наблюдателей, это чисто артефакт для ускоряющегося Боба). Теперь представьте, что вы в корабле рядом с черной дырой. Вся известная вам вселенная - вокруг черной дыры, но поскольку вы висите над черной дырой, ваша система координат аналогична системе координат Боба на последней картинке. И если просто перейти в другую систему координат, как у Алисы (это будет как раз Kruskal), то с другой стороны обнаружится еще столько же пространства-времени, сколько с этой стороны горизонта, еще одна полноценная вселенная, которая в системе координат Боба просто отсутствует. Вот в эту параллельную вселенную и ведут wormholes.
Продолжение следует...
Один вопрос меня живо интересовал, в частности. Вот говорится, что при приближении к черной дыре "время замедляется", и чем ближе к горизонту событий, тем сильнее. Для внешнего наблюдателя падающий в черную дыру корабль по мере приближения к горизонту будет двигаться все медленнее и медленнее и так никогда горизонта не достигнет. Т.е. не просто очень долго будет падать, а вообще _никогда_ не долетит до ЧД. (Будем считать черную дыру постоянной и забьем пока на эффект их испарения, это уже кванты.) А с точки зрения падающего в черную дыру, он туда таки упадет довольно быстро, пересечет горизонт событий и продолжит движение внутрь до самой сингулярности в центре. Но как это возможно, если он подлетает к ЧД бесконечно долго, получается эдакое "никогда, а потом..."? Оказалось, что этот кажущийся парадокс был вызван моим непониманием течения времени, и время - это не прямое шоссе, по которому можно двигаться быстрее или медленнее, а более правильно думать об измеренном времени как о длине пути, и пути могут быть самые разные в разные стороны. Как можно в из одной точки в другую добраться разными путями с разными длинами, и как можно проехать одинаковые расстояния, но оказаться совсем в разных точках, так и со временем, оно зависит от траектории, и одинаковые показания часов еще не означают одновременности событий, в частности.
В одной публичной лекции про черные дыры Susskind упомянул, что эта ситуация с разницей времен падающего в ЧД и внешнего наблюдателя аналогична случаю, где нет никакой черной дыры, пустое плоское пространство, и просто один из наблюдателей равномерно ускоряется и улетает от другого. И действительно ведь, один из вариантов принципа эквивалентности, из которого вся эта теория выросла, гласит, что нахождение в гравитационном поле эквивалентно соответствующему ускорению в пространстве без оного. Двигается ли наша ракета в космосе с ускорением g или стоит на Земле, изнутри определить крайне сложно (на самом деле небольшая разница будет - приливные силы - но если представить однородное гравитационное поле, то она исчезнет). Так вот, упомянутый вариант с ускоряющимся наблюдателем в пустом пространстве известен под именем Rindler coordinates. Что интересно, для его описания достаточно special relativity. Суть такова™. Пусть у нас есть два космонавта, Алиса и Боб. Изначально они вместе висят в пустом пространстве в одной точке. Ровно в 10:00 Боб включает двигатель на своей ракете и начинает удаляться с ускорением 83.3 км/с2 (будем считать, что он опытный штангист и легко выдержит такую перегрузку :) ). Алиса остается на месте. Боб сохраняет постоянное ускорение в его собственной системе координат, т.е. испытывает одну и ту же перегрузку. В системе координат Алисы Боб летит все быстрее и быстрее, и согласно специальной теории относительности время у него тикает все медленее, поэтому его ускорение в системе координат Алисы постепенно уменьшается и по мере приближения скорости к скорости света она растет все медленнее, так никогда и не доходя до скорости света. Поэтому в системе координат Алисы траектория Боба выглядит не как парабола, а как гипербола (X2 - T2 = const). Спустя час, в 11:00 Алиса в точке А прикидывает, сколько времени сейчас показывают часы Боба, который сейчас в точке В. Они уже несколько замедлились, и в этой точке его истории показывают только 10:52. Теперь если мы посмотрим на Боба в точке В, то стоит вспомнить, что дело происходит в пространстве Минковского, и плоскость одновременных ему событий, точки, вектора к которым от него перпендикулярны вектору его движения в пространстве-времени, поворачивается не в ту же сторону, куда вектор скорости, а навстречу ему (в пространстве Минковского вектору (dt, dx) перпендикулярен вектор (dx, dt), т.к. в скалярном произведении у одного из компонентов стоит минус). В результате с т.з. Боба в В ему одновременен момент в истории Алисы, где она в точке С. Там на ее часах только 10:42.

Чем примечательна такая гипербола, в каждой ее точке "перпендикуляр" (в минковском смысле) к касательной проходит через начало координат.
Когда на часах Боба настает 11:00 (точка D), для него одновременен момент Алисы в точке Е, где ее часы показывают 10:45. Когда на часах Боба 12:00, на часах Алисы с его т.з. 10:57. В системе координат Боба часы Алисы тикают все медленнее и медленнее и никогда они не достигнут отметки 11:00. Траектория Боба уходит вверх и вправо в бесконечность, стремясь к диагональной линии, но никогда ее не достигая. Его плоскости одновременности проходят от него к началу координат и тоже никогда не достигнут диагонали T=X. Эта диагональ - горизонт событий для Боба. Любое событие за ним, например F, никогда не настанет для Боба, и свет от него никогда к нему не придет. На ровном месте в пустом пространстве мы получили горизонт событий, ведущий себя ровно как горизонт черной дыры. Можно представить, что Боб на самом деле стоит на месте в постоянном гравитационном поле, а Алиса свободно падает в сторону горизонта (у нее всю дорогу невесомость, кстати) и дальше. Во многом эта ситуация действительно совпадает со сценарием черной дыры, для черной дыры есть точно такой же график с гиперболами и плоским горизонтом, просто координаты чуть иначе определяются (Kruskal coordinates). Тут становится видно, как сочетаются утверждения, что свободно падающая Алиса горизонт вообще не замечает, проходит его спокойно в 11:00 и для нее ничего не происходит, в то время как для "внешнего наблюдателя" Боба она замедляется и практически замирает, так никогда и не доходя до горизонта. Еще можно посмотреть на лучи света, испускаемые ими (желтенькие на картинке). Отметки на траекториях Алисы и Боба расставлены с равными интервалами по их часам. Видно, что как Боб видит Алисино время замедленным, так и Алиса видит Боба замедленным. В интернетах порой можно встретить описания падения в черную дыру, где говорят, что из-за "замедления времени" при приближении к оной можно увидеть, как вселенная вокруг ускоряет свой ход. Так вот, это неправда, вселенная вокруг будет выглядеть также замедленной (но не очень сильно, т.к. долго полюбоваться замедлением не выйдет, сингулярность тебя встретит за весьма ограниченное время).
Вот если взять двух наблюдателей, зависших над черной дырой, или что то же самое двух ускоряющихся в пустом пространстве Боба и Чарли, то там уже действительно Чарли, который "выше" (= у него ускорение меньше) будет видеть Боба замедленным, а Боб будет видеть Чарли ускоренным. Это как раз похоже на то, что в кино было.

В случае Rindler coordinates, если ускорения Боба и Чарли связаны с их начальным положением как g = c2/X, то в их собственных системах координат они будут оба неподвижны относительно друг друга. Это как раз аналог двух зависших на разных высотах над массивным телом наблюдателей.
Еще у меня есть картинка, как в системе координат Боба будет выглядеть "падение" Алисы.

Она сперва будет удаляться с ускорением, потом начнет замедляться и будет все медленнее и медленнее приближаться к горизонту, обозначенному тут красной линией. Что занятно, и уже понятно из вышеописанного, на этом графике, даже если продлить его вверх в бесконечность, отражен лишь первый час истории Алисы, а ее достижение горизонта и дальнейшая судьба в этих координатах отстутствует вовсе. Серые линии показывают, во что превратилась регулярная сетка координат Алисы. Они так ловко загибаются, что как ни двигайся по ним в пространстве и времени, на красную линию горизонта не попадешь. Этот момент, что в одних координатах у нас может быть принципиально больше разных мест и событий, чем в других, лежит в основе далеко идущих предсказаний о wormholes. Вот на графиках выше у нас есть обычное пространство-время с обеих сторон от горизонта (который ничем особенным и не является для Алисы и многих других наблюдателей, это чисто артефакт для ускоряющегося Боба). Теперь представьте, что вы в корабле рядом с черной дырой. Вся известная вам вселенная - вокруг черной дыры, но поскольку вы висите над черной дырой, ваша система координат аналогична системе координат Боба на последней картинке. И если просто перейти в другую систему координат, как у Алисы (это будет как раз Kruskal), то с другой стороны обнаружится еще столько же пространства-времени, сколько с этой стороны горизонта, еще одна полноценная вселенная, которая в системе координат Боба просто отсутствует. Вот в эту параллельную вселенную и ведут wormholes.
Продолжение следует...