ATS madness: smoothsort с доказательством
Церебральный секс в 7 актах.
В ЖЖ модно проходить психологические тесты, один из них в этом посте, суть его раскрывается ниже.
Введение
Для тренировки своего ATS-фу я решил реализовать и доказать на нем алгоритм smoothsort - сортировку, имеющую сложность O(n * log n) как в среднем, так и в худшем случае, O(n) в лучшем, и вроде как плавно изменяющую скорость по мере перехода от лучшего случая к среднему (по мере увеличения числа элементов не на своих местах), отсюда ее название. Моей задачей было получить корректно работающую реализацию, содержащую в явном виде доказательство отсортированности получаемого массива. Заставить ее работать супер быстро я задачу не ставил, т.к. по-любому константа в сложности этого алгоритма так велика, что на практике он проигрывает по скорости более простым методам на малых объемах и гибридным на больших. Поэтому я позволил себе неэффективную реализацию с использованием O(log n) памяти под вспомогательные структуры. В интернетах пишут, что Аллах послал нам эту сортировку через пророка своего Дейкстру в варианте с О(1) дополнительной памяти, но это все равно враки, потом расскажу подробней почему.
Акт 1. Алгоритм
Алгоритм строится вокруг упоминавшихся тут ранее чисел Леонардо. Напомню, что определяются они так:
L[0] = 1, L[1] = 1, L[k] = L[k-1] + L[k-2] + 1
Вводится понятие кучи Леонардо - это неявная структура, содержащая L[k] элементов. Для k=0 и k=1 она состоит из единственного элемента. Для k > 1 куча Леонардо состоит из трех идущих подряд частей: кучи размером L[k-1], кучи размером L[k-2] и одного элемента, называемого корнем (для кучи из одного элемента ее корнем считается он сам). Такая куча имеет размер L[k-1] + L[k-2] + 1 = L[k], т.е. ее устройство повторяет определение чисел Леонардо. Структура неявная, т.е. все элементы лежат подряд в обычном массиве, просто мы мысленно разбиваем их на группы и интерпретируем как кучи.
Не каждое натуральное число является числом Леонардо, но любое натуральное число можно представить в виде суммы чисел Леонардо с разными индексами. Мы это вскоре докажем конструктивно в нашем коде. Поэтому массив любой длины мы можем "покрыть" идущими подряд кучами Леонардо с убывающими индексами (k). Такую последовательность кучек Леонардо назовем рядом куч (heap string). И чтобы это все было не зря, потребуем от этих неявных структур несколько свойств. Свойством кучи Леонардо (heap property) сделаем требование, чтобы ее корень всегда был не меньше, чем корни двух входящих в нее подкуч (если они есть). А свойством ряда куч (heap string property) сделаем требование неубывания корней кучек, из которых этот ряд состоит. Вот так, например, выглядит ряд куч Леонардо на массиве из 10 элементов:
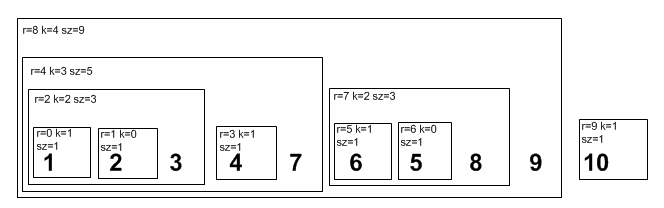
В этом ряду две кучи, одна имеет размер sz=9, индекс k=4, ее корнем является элемент с индексом r=8. Вторая куча состоит из одного элемента с позицией r=9, имеет размер sz=1 и индекс k=1. Первая куча размером L[4] внутри имеет две подкучи размерами L[3] и L[2], которые содержат подкучи меньшего размера и т.д. Для каждой кучи выполнено ее свойство - корень не меньше корней подкуч, и для всего ряда выполнено свойство ряда - корни входящих в него куч не убывают. В итоге сам массив еще не отсортирован, но уже какой-то порядок в нем есть. Можно заметить, что следствием свойства кучи является тот факт, что среди всех входящих в нее элементов максимальный - самый правый. Такое же следствие и у свойства ряда куч - самый правый элемент больше всех (не меньше, если быть точным).
Отсюда уже несложно угадать устройство smoothsort'a. Мы берем массив и сперва проходимся по нему слева-направо, постепенно с нуля строя ряд куч, добавляя в него по одному элементу и обеспечивая выполнение требуемых свойств. В результате максимальный элемент занимает свое место - самое правое. Потом мы идем обратно справа-налево, выкидывая по элементу и сокращая ряд куч, так же обеспечивая выполнение обоих свойств. Тогда на каждом шагу этого обратного хода максимальный элемент из всех, входящих в ряд, оказывается справа, а ряд на каждом шагу сокращается. В результате, если у нас массив A из n элементов, то после построения ряда из n элементов у нас элементы A[0..n-2] не больше, чем A[n-1], потом после сокращения ряда на 1 элементы A[0..n-3] не больше, чем A[n-2], ..., и когда ряд сократится до двух элементов, получится, что A[0] <= A[1] <= A[2] ... <= A[n-1], т.е. массив окажется отсортированным. Всего будет почти 2n шагов, каждый из которых потребует не более O(log n) действий, что доказано elsewhere (любимое слово Hongwei Xi), поэтому общая сложность O(n * log n).
Неупомянутые детали. Каким образом происходит рост ряда куч при добавлении одного элемента? Мы смотрим на две самых правых кучи. Если их индексы - соседние убывающие числа (например, 3 и 2 или 1 и 0), то из двух этих куч и нового элемента мы делаем одну кучу большего размера. В противном случае просто добавляем кучу из одного этого нового элемента, а индексом ее считаем 0, если последняя куча в ряду имела индекс 1 (чтобы получились подряд идущие кучи с индексами 1 и 0), и 1 иначе. Сокращение ряда на один элемент еще проще. Если самая правая куча имеет размер 1, то просто ее выкидываем. Если ее размер больше 1, то она состоит из двух подкуч и корневого элемента. Ставим вместо нее в ряд две эти подкучи, а корневой элемент оказывается выкинутым. После каждой такой операции нужно восстановить требуемые свойства, об этом позже.
Теперь давайте запишем это все на ATS. Мы хотим описать функцию с таким заголовком:
fn {a:t@ype} smoothsort {n:nat | n > 0}
(A : array(a,n), n : int n, gt : gt(a)): (SORTED(0,n-1) | void)
где
typedef gt (a:t@ype) = (a,a) -> bool // x > y
Для любого типа данных a наша полиморфная функция smoothsort принимает массив А из n элементов типа a, количество элементов n и функцию сравнения элементов gt, возвращающую true, когда первый аргумент больше второго. Функция сортирует массив на месте, и ничего не возвращает (void), а вместе с этим ничего она возвращает доказательство утверждения SORTED(0, n-1), т.е. что элементы массива с индексами от 0 до n-1 включительно теперь отсортированы. Будем считать, что сортируем массив по возрастанию, сортировка по убыванию получается просто передачей на вход другой функции сравнения.
Акт 2. Вспомогательные теоремы
Как определить утверждение о сортированности массива или его части? Для этого нам потребуются утверждения об отношениях между отдельными элементами. Поскольку во всем алгоритме мы оперируем одним единственным массивом элементов А, то мы не будем его включать в определения утверждений и доказательств, мы будем просто понимать, что все эти утверждения именно о нем. Определим для начала утверждение о том, что один элемент нашего массива не больше другого (Less Than or Equal):
// LTE(i,j) means A[i] <= A[j]
dataprop LTE(int, int) =
| {i,j:nat} LTEcompared(i,j)
| {k:nat} LTErefl(k,k)
Описание утверждения похоже на описание алгебраического типа данных, только его конструкторы строят не данные, а доказательства. Отношение "меньше или равно" рефлексивно: для любого элемента с индекcом k этот элемент не больше сам себя, и мы можем сконструировать этот факт (LTErefl "типа" LTE(k,k) ) из ничего. Для двух же произвольных элементов мы можем их сравнить между собой переданной нам функцией сравнения и произвести факт-доказательство того, что один не больше другого. Например, можно описать такую функцию упорядочивания пары элементов:
//returns true if a swap occured
fn {a:t@ype} order_elements {n,i,j:nat | j < n; i <= j}
(A: array(a,n), i : int i, j : int j, gt : gt(a)): (LTE(i,j) | bool) =
if A[i] \gt A[j] then
let val tmp = A[i] in A[i] := A[j]; A[j] := tmp;
(LTEcompared | true)
end
else (LTEcompared | false)
Она принимает массив А из n элементов, индексы i и j, такие что первый не больше (левее) второго и оба меньше n, функцию сравнения gt, и упорядочивает элементы A[i] и A[j], возвращая признак того, произошла ли перестановка, а также доказательство утверждения LTE(i,j), т.е. что теперь A[i] <= A[j]. У нас будет всего пара таких простых функций, производящих сравнение элементов и конструирующих доказательства утверждений о том, что один элемент не больше другого. В силу тривиальности этих функций их корректность легко проверить вручную. Вызов этих функций будет единственным способом получить такие доказательства, и также единственным местом, где будут производиться какие-либо изменения в нашем массиве. Это даст нам уверенность в том, что утверждения об элементах массива действительно соответствуют фактическому положению дел, несмотря на то, что непосредственно их доказательства не включают в себя реальные значения из массива, т.е. связь между ними не железобетонная.
Отношение "меньше или равно" транзитивно, этот факт можно описать аксиомой:
praxi lte_trans {a,b,c:nat} (ab : LTE(a,b), bc : LTE(b,c)): LTE(a,c)
Она гласит: если у нас есть доказательство ab утверждения LTE(a,b) (т.е., что A[a] <= A[b]) и доказательство bc утверждения LTE(b,c), то справедливо утверждение LTE(a,c), т.е. A[a] <= A[c]. lte_trans - функция, принимающая два факта-доказательства и возвращающая новый факт-доказательство. Ключевое слово praxi говорит, что это аксиома, и тела функции (конструктивного доказательства) не будет.
Имея утверждения об упорядоченности элементов, можно определить понятие отсортированности куска массива (по возрастанию). Кусок из единственного элемента всегда отсортирован, это тривиальный случай, служащий базой индукции. Если доказано, что кусок массива A[i..j] отсортирован, и доказано, что A[i-1] <= A[i], то учитывая транзитивность сравнения, кусок массива A[i-1 .. j] тоже отсортирован по возрастанию. Записывается это так:
//SORTED(i,j) means A[i..j] is sorted
dataprop SORTED(int, int) =
| {k:nat} SORTEDsingle(k,k)
| {i,j:nat | i > 0; i <= j} SORTEDjoin(i-1, j) of (LTE(i-1,i), SORTED(i,j))
Наша функция сортировки должна будет построить конструктивно доказательство утверждения SORTED(0, n-1). Поскольку мы не определили такое утверждение для пустых массивов, а только начиная с одного элемента, наша функция сортировки будет принимать только непустые массивы, что отражено в ее заголовке.
В процессе доказательства нам пригодится еще один вид утверждений: о том, что в некотором куске массива самый правый его элемент не меньше других (максимален), это то свойство, которым обладают правильные кучи Леонардо, а также правильный ряд куч. Устроено оно похожим образом. Для куска из одного элемента это свойство выполнено автоматически. А если у нас доказано, что среди элементов A[i..j] максимальный элемент самый правый, и что A[i-1] <= A[j], то и среди элементов A[i-1 .. j] тоже самый правый элемент максимальный.
// MAXRIGHT(i,j) means A[j] is the max of A[i..j]
dataprop MAXRIGHT(int, int) =
| {k:nat} MRsingle(k,k)
| {i,j:nat | i <= j; i > 0} MRgrow_l(i-1,j) of (LTE(i-1,j), MAXRIGHT(i,j))
Нам также пригодятся несколько простых вспомогательных теорем.
Во-первых, если среди элементов A[i..j] самый правый максимальный, то он не меньше любого из элементов A[i..j]. Для нас это очевидно, а компилятору нужно предъявить явное доказательство:
prfun lte_from_maxright {i,j,k:nat | i <= k; k <= j} ..
(mr: MAXRIGHT(i,j), k: int k, i: int i, j: int j): LTE(k,j) =
case+ mr of
| MRsingle () => LTErefl
| MRgrow_l(lte_ij, mr_i1j) =>
if k = i then lte_ij else lte_from_maxright(mr_i1j, k, i+1, j)
Ключевое слово prfun определяет рекурсивную функцию-доказательство, производящую факт-доказательство некоторого утверждения. В данном случае функция lte_from_maxright принимает доказательство mr утверждения MAXRIGHT(i,j), сами числа i и j, а также индекс k, заключенный между ними, и возвращает доказательство утверждения LTE(k,j), т.е. что A[k] <= A[j]. Тело функции-теоремы состоит из анализа случаев того, чем может быть mr. Паттерн-матчинг то бишь. Знак "+" после case означает обязательную проверку на exhaustiveness анализа, чтобы компилятор выдал ошибку, если мы какой-то возможный случай забыли рассмотреть. Фактически, доказательство MAXRIGHT(i,j) состоит из тривиального факта о j-том элементе и множестве фактов LTE(x,j). Перебирая их один за одним, мы найдем тот, где x будет равен k, это будет искомый факт. Ежели факт mr представлен вариантом MRsingle, то это тривиальный случай куска из единственного элемента, и мы можем применить рефлексивность нашего отношения и использовать LTErefl. Если же mr представлен вариантом MRgrow_l, т.е. построен из доказательств утверждений LTE(i,j) и MAXRIGHT(i+1, j), которые мы посредством паттерн-матчинга поименовали lte_ij и mr_i1j, то ежели k = i, то значит LTE(i,j) есть LTE(k,j), искомое утверждение, и имеющийся факт lte_ij его доказывает, его-то и вернем. А если i еще не равно k, то рекурсивно вызываем себя для mr_i1j : MAXRIGHT(i+1, j).
Рекурсивные функции-теоремы обязаны завершаться, ведь если такая функция зациклится, то нужное значение так и не найдет, и значит теорема не доказана. Поэтому тут требуется указать метрику завершимости - уменьшающееся при каждом рекурсивном вызове натуральное число. В данном случае это j - i, т.к. j не меняется, а i растет.
Функции-теоремы очень похожи на обычные функции, просто вместо данных там факты, а вместо их типов - утверждения, которые те доказывают. Однако главное отличие в том, что функции-теоремы используются только в момент компиляции, в конечный код они не попадают. Причем, они вообще никогда на самом деле не исполняются, им ведь главное типизироваться и не содержать ошибок. Если все варианты рассмотрены, и в каждом варианте все статические условия выполнены, то функция корректна, теорема доказана. Писать код, старательно доказывать компилятору его корректность, осознавая, что он все равно превратится в no-op, - не это ли благородное недеяние, воспетое древними мудрецами? Нет, не это. Но близко.
Еще одна теорема, которая нам пригодится. Если у двух подряд идущих кусков массивов максимальные элементы самые правые, и из этих двух локальных максимумов правый не меньше левого, то в силу транзитивности сравнения мы можем объединить два куска массива в один, и в нем тоже максимальный элемент будет самым правым. Записывается доказательство такой теоремы так:
prfn mr_join {a,b,c:nat | a <= b; b < c}
(ab: MAXRIGHT(a,b), bc: MAXRIGHT(b+1, c), lte_bc: LTE(b,c),
a: int a, b: int b): MAXRIGHT(a,c) = let
prfun loop {i:nat | i >= a; i <= b+1} .. (i: int i, mr_ic: MAXRIGHT(i,c)): MAXRIGHT(a,c) =
if i=a then mr_ic else
loop(i-1, MRgrow_l(lte_trans(lte_from_maxright(ab, i-1, a, b), lte_bc), mr_ic))
in
loop(b+1, bc)
end
Строится доказательство в цикле. Берем факт bc о том, что у правого куска (A[b+1..c]) самый правый элемент максимален, и по-одному элементу расширяем его влево: каждый очередной элемент из левого куска A[a..b] не больше A[b] (тут мы используем предыдущую теорему lte_from_maxright), а тот не больше, чем A[c] (это дано в условии в виде факта lte_bc: LTE(b,c) ), поэтому используя аксиому о транзитивности lte_trans получаем доказательство LTE(i-1, c), его прилепляем слева к текущему и получаем MAXRIGHT(i-1,c), пока не получим MAXRIGHT(a,c), который и требовалось получить.
Ну и еще одна теорема, простое следствие из предыдущей. Если в некотором куске массива A[a..b] самый правый элемент максимален, а следующий за ним элемент A[b+1] еще больше, то среди элементов A[a..b+1] самый правый максимальный.
prfn mr_grow_r {a,b:nat | a <= b}
(ab: MAXRIGHT(a,b), pf_lte: LTE(b,b+1), a: int a, b: int b): MAXRIGHT(a,b+1) = let
prval b1 : MAXRIGHT(b+1,b+1) = MRsingle
in
mr_join(ab, b1, pf_lte, a, b)
end
Ключевое слово prfn означает нерекурсивную функцию-теорему, для нее метрика завершимости не нужна. И так понятно, что она завершается, ибо внутри могут использоваться только завершающиеся функции-теоремы.
Акт 3. Структуры с гарантиями
Для реализации алгоритма нам потребуется хранить информацию о текущем устройстве ряда куч Леонардо в массиве. Некоторые реализации используют для этого битовый вектор, вычисляя необходимые параметры на ходу, но мы будем использовать более явную, наглядную и подробную структуру. Одна куча Леонардо у нас будет описываться структурой из трех чисел, ее характеризующих: индекс k, размер sz, равный L[k], и позиция корневого элемента в массиве, определяющая расположение кучи. Ряд куч будет описываться односвязным списком таких структур. Кроме данных структуры будут включать в себя факты об этих данных, это обеспечит корректность структур, ведь далеко не любая тройка чисел описывает правильную кучу Леонардо. Требуя предоставить доказательства, компилятор не даст нам создать неправильную структуру. Например, факт того, что sz=L[k], будет выражен явно доказательством утверждения LEON(k,sz). Само это утверждение определено так (мы это уже делали в прошлых сериях):
dataprop LEON(int, int) = //LEON(n,x) means L[n] = x
| {n:nat | n <= 1} LEONbase(n, 1)
| {n:nat | n > 1; a,b:nat | a > 0; b > 0} LEONind(n, a+b+1) of (LEON(n-2, a), LEON(n-1,b))
Кроме того, нам надо связать между собой значения root (позиция корневого элемента) и sz (размер кучи): root не может быть меньше, чем sz-1, а sz не может быть меньше 1. Опишем такое утверждение:
dataprop LH(int, int) = //LH(r,sz) means r >= sz - 1, r>=0, sz>=1
{r,sz:nat | sz >= 1; r >= sz - 1} LHpf(r,sz)
Задание предусловий перед конструктором не позволит его использовать, если условия не выполнены. Имея доказательство LHpf утверждения LH(r,sz), мы можем "извлечь" эти условия:
prfn lh_use {r,sz:int} (pf : LH(r, sz)): [r >= sz-1; sz >= 1] void =
case pf of LHpf () => ()
Здесь функция-теорема lh_use возвращает "ничто", void, снабженное несколькими статическими неравенствами. Тело ее состоит из "анализа вариантов": если передан такой-то конструктор, то его предусловия были выполнены, а значит они истинны и сейчас.
Итак, куча Леонардо, имеющая правильную форму, но для которой необязательно выполнено свойство кучи (про корень), будет описываться так:
typedef heap(r:int, k:int, sz:int) =
@{root = int r, k = int k, sz = int sz, pf_sz = LEON(k,sz), pf_r = LH(r,sz), pf_gc = GOODCHILDREN(k)}
Она состоит из трех целых чисел и доказательств некоторых утвеждений о них. Последнее из утверждений будет описано чуть позже.
Если для кучи выполнено ее свойство (корень не меньше корней подкуч), то корень ее является не только самым правым элементом, но и максимальным. Структуру, состоящую из кучи Леонардо и доказательства выполненности этого свойства, назвомем heap1:
typedef heap1(r:int, k:int, sz:int) =
@{ hp = heap(r,k,sz), pf_mr = MAXRIGHT(r-sz+1, r) }
Если для ряда куч выполнено свойство ряда (корни не убывают), то для каждой кучи в нем справедливо утверждение, что ее корень - самый правый и максимальный элемент всего ряда от начала до текущей кучи. Добавим в структуру доказательство такого факта, получим heap2:
typedef heap2(r:int, k:int, sz:int) =
@{ hp = heap(r,k,sz), pf_mr = MAXRIGHT(r-sz+1, r), pf_totalmr = MAXRIGHT(0,r) }
Именно из таких структур будет состоять список, определяющий правильный ряд куч Леонардо. Но в такой список нельзя добавлять что попало (например, один и тот же элемент), между позициями корней соседних элементов есть вполне определенная связь: они отличаются ровно на размер очередной кучи. Если m - общее число элементов в ряде куч, то ряд можно описать так:
datatype heaps(int) =
| heaps_nil (0)
| {m,r,k,sz:nat | m + sz - 1 == r} heaps_cons (r+1) of (heap2(r,k,sz), heaps(m))
#define :: heaps_cons
#define nil heaps_nil
В пустом ряду 0 элементов. Если есть ряд из m элементов и куча (со всеми свойствами) из sz элементов, то ее корень должен иметь быть на позиции m + sz - 1. Только если это условие выполнено, мы сможем добавить очередную кучу в наш ряд. Ряд куч представлен "списком", который синтаксически "растет" влево (как обычно это делают списки в функциональных языках), но логически в массиве ряд растет вправо: голова списка является последней, самой правой кучей.
Акт 4. Еще о числах Леонардо
В процессе работы нам понадобится уметь строить кучи Леонардо из двух меньших куч и нового корневого элемента, а также разбивать обратно большую кучу на две маленьких и корень. Позиции корней подкуч вычисляются через числа Леонардо, и чтобы компилятор был уверен, что мы не вылезем за пределы массива в ходе таких операций, нам понадобится ряд теорем.
Чтобы из двух куч и нового элемента сделать одну большую, нужно из доказательств о том, что размеры тех куч являются числами Леонардо, сделать доказательство, что размер новой тоже является нужным числом Леонардо. Для этого используется конструктор LEONind, но в его предусловиях требуется положительность значений. Ее можно извлечь из фактов-аргументов с помощью такой теоремы:
prfn leon_positive {n,x:nat} (pf : LEON(n,x)): [x > 0] void =
case+ pf of
| LEONbase () => ()
| LEONind(pf1, pf2) => ()
Вновь анализ вариантов и использование информации о соответствующих вариантам предусловиях. Выглядит функция-доказательство так, будто в ней ничего не делается, однако ж делается, просто за кадром. Еще забавнее это выглядит в следующей теореме:
prfun leon_isfun {n,x1,x2:nat} .. (pf1 : LEON(n,x1), pf2 : LEON(n,x2)): [x1==x2] void =
case+ (pf1, pf2) of
| (LEONbase (), LEONbase ()) => ()
| (LEONind(p1a,p1b), LEONind(p2a,p2b)) => let
prval () = leon_isfun(p1a, p2a)
prval () = leon_isfun(p1b, p2b)
in () end
Тут мы доказываем, что L[k] - функция в математическом смысле, т.е. Если x=y, то L[x]=L[y]. Теорема получает два факта (LEON(n,x1) и LEON(n,x2)) и доказывает, что x1==x2. Опять разбор вариантов и сопоставление аргументов. Если оба факта - LEONbase, то имеют "тип" LEON(n,1), т.е. x1=1 и x2=1, а значит x1==x2. Если оба - LEONind, то содержат вполне определенные доказательства, которые можно сопоставить друг с другом рекурсивно. А разные конструкторы pf1 и pf2 иметь не могут, т.к. у разных конструкторов взаимоисключающие предусловия на n, так что нерассмотренных вариантов в case+ не возникает, и компилируется такое доказательство без ошибок. Используется оно в теореме о монотонности L[x]:
prfn leon_mono {k1,sz1,sz2:nat | k1 > 0}
(pf1 : LEON(k1, sz1), pf2 : LEON(k1 + 1,sz2)): [sz1 < sz2-1] void = let
prval LEONind(pf2_2, pf2_1) = pf2
prval () = leon_isfun(pf1, pf2_1)
in () end
Тут доказывается, что после единицы каждое следующее число Леонардо больше предыдущего (как минимум на 2). Что тут происходит: В предусловии сказано, что k1 > 0, значит k1 + 1 > 1, значит pf2 имеет вид LEONind(...), и паттерн-матчингом в первой строке мы извлекаем входящие в него доказательства, которые назовем pf2_2 и pf2_1. Если вспомнить определение LEONind, видно, что они имеют "тип" LEON(k1 + 1 - 2, x1) и LEON(k1 + 1 - 1, x2) соответственно, где x1 и x2 - некоторые натуральный числа. Получается, что у pf2_1 и исходного аргумента pf1 похожий "тип" - они оба LEON(k1, ...), т.е. утверждения о числе L[k1]. Теперь мы задействуем теорему leon_isfun, которая устанавливает равенство значений L[k1], т.е. sz1==x2. Но из определения LEON(k1 + 1,sz2) компилятор знает, что sz2 = x1 + x2 + 1, а значит sz2 = x1 + sz1 + 1, где x1 - некоторое натуральное число, а значит sz1 < sz2-1, ч.т.д.
Еще одна похожая теорема: если для натуральных чисел k,sz, sz1 и sz2, таких что k > 1 и sz2 == sz - 1 - sz1, у нас есть доказательство, что L[k]=sz, а L[k-1]=sz1, то L[k-2]=sz2. Это нужно при вычислении размеров подкуч: если мы знаем размер большой кучи L[k] и вычислили размер одной из подкуч L[k-1], то размер второй подкучи L[k-2] можем получить вычитанием.
prfn leon_size_dif {k,sz, sz1, sz2 : nat | k > 1; sz2 == sz - 1 - sz1}
(pfsz : LEON(k,sz), pfsz1 : LEON(k-1,sz1)) : LEON(k-2, sz2) =
case+ pfsz of
| LEONind(pf_2, pf_1) => let prval () = leon_isfun(pf_1, pfsz1) in pf_2 end
Способ доказательства практически идентичен предыдущей теореме.
Ну и еще одна мелочь, которая потребуется в коде: доказательство того, что для k < 2 L[k]=1.
prfn leon_base_is1 {k,sz:nat | k < 2} (pf : LEON(k,sz)): [sz==1] void =
case+ pf of LEONbase () => ()
Анализ вариантов исчерпывается единственным случаем в силу условия на k, и из определения LEONbase компилятор извлекает требуемый факт.
Продолжение...
В ЖЖ модно проходить психологические тесты, один из них в этом посте, суть его раскрывается ниже.
Введение
Для тренировки своего ATS-фу я решил реализовать и доказать на нем алгоритм smoothsort - сортировку, имеющую сложность O(n * log n) как в среднем, так и в худшем случае, O(n) в лучшем, и вроде как плавно изменяющую скорость по мере перехода от лучшего случая к среднему (по мере увеличения числа элементов не на своих местах), отсюда ее название. Моей задачей было получить корректно работающую реализацию, содержащую в явном виде доказательство отсортированности получаемого массива. Заставить ее работать супер быстро я задачу не ставил, т.к. по-любому константа в сложности этого алгоритма так велика, что на практике он проигрывает по скорости более простым методам на малых объемах и гибридным на больших. Поэтому я позволил себе неэффективную реализацию с использованием O(log n) памяти под вспомогательные структуры. В интернетах пишут, что Аллах послал нам эту сортировку через пророка своего Дейкстру в варианте с О(1) дополнительной памяти, но это все равно враки, потом расскажу подробней почему.
Акт 1. Алгоритм
Алгоритм строится вокруг упоминавшихся тут ранее чисел Леонардо. Напомню, что определяются они так:
L[0] = 1, L[1] = 1, L[k] = L[k-1] + L[k-2] + 1
Вводится понятие кучи Леонардо - это неявная структура, содержащая L[k] элементов. Для k=0 и k=1 она состоит из единственного элемента. Для k > 1 куча Леонардо состоит из трех идущих подряд частей: кучи размером L[k-1], кучи размером L[k-2] и одного элемента, называемого корнем (для кучи из одного элемента ее корнем считается он сам). Такая куча имеет размер L[k-1] + L[k-2] + 1 = L[k], т.е. ее устройство повторяет определение чисел Леонардо. Структура неявная, т.е. все элементы лежат подряд в обычном массиве, просто мы мысленно разбиваем их на группы и интерпретируем как кучи.
Не каждое натуральное число является числом Леонардо, но любое натуральное число можно представить в виде суммы чисел Леонардо с разными индексами. Мы это вскоре докажем конструктивно в нашем коде. Поэтому массив любой длины мы можем "покрыть" идущими подряд кучами Леонардо с убывающими индексами (k). Такую последовательность кучек Леонардо назовем рядом куч (heap string). И чтобы это все было не зря, потребуем от этих неявных структур несколько свойств. Свойством кучи Леонардо (heap property) сделаем требование, чтобы ее корень всегда был не меньше, чем корни двух входящих в нее подкуч (если они есть). А свойством ряда куч (heap string property) сделаем требование неубывания корней кучек, из которых этот ряд состоит. Вот так, например, выглядит ряд куч Леонардо на массиве из 10 элементов:

В этом ряду две кучи, одна имеет размер sz=9, индекс k=4, ее корнем является элемент с индексом r=8. Вторая куча состоит из одного элемента с позицией r=9, имеет размер sz=1 и индекс k=1. Первая куча размером L[4] внутри имеет две подкучи размерами L[3] и L[2], которые содержат подкучи меньшего размера и т.д. Для каждой кучи выполнено ее свойство - корень не меньше корней подкуч, и для всего ряда выполнено свойство ряда - корни входящих в него куч не убывают. В итоге сам массив еще не отсортирован, но уже какой-то порядок в нем есть. Можно заметить, что следствием свойства кучи является тот факт, что среди всех входящих в нее элементов максимальный - самый правый. Такое же следствие и у свойства ряда куч - самый правый элемент больше всех (не меньше, если быть точным).
Отсюда уже несложно угадать устройство smoothsort'a. Мы берем массив и сперва проходимся по нему слева-направо, постепенно с нуля строя ряд куч, добавляя в него по одному элементу и обеспечивая выполнение требуемых свойств. В результате максимальный элемент занимает свое место - самое правое. Потом мы идем обратно справа-налево, выкидывая по элементу и сокращая ряд куч, так же обеспечивая выполнение обоих свойств. Тогда на каждом шагу этого обратного хода максимальный элемент из всех, входящих в ряд, оказывается справа, а ряд на каждом шагу сокращается. В результате, если у нас массив A из n элементов, то после построения ряда из n элементов у нас элементы A[0..n-2] не больше, чем A[n-1], потом после сокращения ряда на 1 элементы A[0..n-3] не больше, чем A[n-2], ..., и когда ряд сократится до двух элементов, получится, что A[0] <= A[1] <= A[2] ... <= A[n-1], т.е. массив окажется отсортированным. Всего будет почти 2n шагов, каждый из которых потребует не более O(log n) действий, что доказано elsewhere (любимое слово Hongwei Xi), поэтому общая сложность O(n * log n).
Неупомянутые детали. Каким образом происходит рост ряда куч при добавлении одного элемента? Мы смотрим на две самых правых кучи. Если их индексы - соседние убывающие числа (например, 3 и 2 или 1 и 0), то из двух этих куч и нового элемента мы делаем одну кучу большего размера. В противном случае просто добавляем кучу из одного этого нового элемента, а индексом ее считаем 0, если последняя куча в ряду имела индекс 1 (чтобы получились подряд идущие кучи с индексами 1 и 0), и 1 иначе. Сокращение ряда на один элемент еще проще. Если самая правая куча имеет размер 1, то просто ее выкидываем. Если ее размер больше 1, то она состоит из двух подкуч и корневого элемента. Ставим вместо нее в ряд две эти подкучи, а корневой элемент оказывается выкинутым. После каждой такой операции нужно восстановить требуемые свойства, об этом позже.
Теперь давайте запишем это все на ATS. Мы хотим описать функцию с таким заголовком:
fn {a:t@ype} smoothsort {n:nat | n > 0}
(A : array(a,n), n : int n, gt : gt(a)): (SORTED(0,n-1) | void)
где
typedef gt (a:t@ype) = (a,a) -> bool // x > y
Для любого типа данных a наша полиморфная функция smoothsort принимает массив А из n элементов типа a, количество элементов n и функцию сравнения элементов gt, возвращающую true, когда первый аргумент больше второго. Функция сортирует массив на месте, и ничего не возвращает (void), а вместе с этим ничего она возвращает доказательство утверждения SORTED(0, n-1), т.е. что элементы массива с индексами от 0 до n-1 включительно теперь отсортированы. Будем считать, что сортируем массив по возрастанию, сортировка по убыванию получается просто передачей на вход другой функции сравнения.
Акт 2. Вспомогательные теоремы
Как определить утверждение о сортированности массива или его части? Для этого нам потребуются утверждения об отношениях между отдельными элементами. Поскольку во всем алгоритме мы оперируем одним единственным массивом элементов А, то мы не будем его включать в определения утверждений и доказательств, мы будем просто понимать, что все эти утверждения именно о нем. Определим для начала утверждение о том, что один элемент нашего массива не больше другого (Less Than or Equal):
// LTE(i,j) means A[i] <= A[j]
dataprop LTE(int, int) =
| {i,j:nat} LTEcompared(i,j)
| {k:nat} LTErefl(k,k)
Описание утверждения похоже на описание алгебраического типа данных, только его конструкторы строят не данные, а доказательства. Отношение "меньше или равно" рефлексивно: для любого элемента с индекcом k этот элемент не больше сам себя, и мы можем сконструировать этот факт (LTErefl "типа" LTE(k,k) ) из ничего. Для двух же произвольных элементов мы можем их сравнить между собой переданной нам функцией сравнения и произвести факт-доказательство того, что один не больше другого. Например, можно описать такую функцию упорядочивания пары элементов:
//returns true if a swap occured
fn {a:t@ype} order_elements {n,i,j:nat | j < n; i <= j}
(A: array(a,n), i : int i, j : int j, gt : gt(a)): (LTE(i,j) | bool) =
if A[i] \gt A[j] then
let val tmp = A[i] in A[i] := A[j]; A[j] := tmp;
(LTEcompared | true)
end
else (LTEcompared | false)
Она принимает массив А из n элементов, индексы i и j, такие что первый не больше (левее) второго и оба меньше n, функцию сравнения gt, и упорядочивает элементы A[i] и A[j], возвращая признак того, произошла ли перестановка, а также доказательство утверждения LTE(i,j), т.е. что теперь A[i] <= A[j]. У нас будет всего пара таких простых функций, производящих сравнение элементов и конструирующих доказательства утверждений о том, что один элемент не больше другого. В силу тривиальности этих функций их корректность легко проверить вручную. Вызов этих функций будет единственным способом получить такие доказательства, и также единственным местом, где будут производиться какие-либо изменения в нашем массиве. Это даст нам уверенность в том, что утверждения об элементах массива действительно соответствуют фактическому положению дел, несмотря на то, что непосредственно их доказательства не включают в себя реальные значения из массива, т.е. связь между ними не железобетонная.
Отношение "меньше или равно" транзитивно, этот факт можно описать аксиомой:
praxi lte_trans {a,b,c:nat} (ab : LTE(a,b), bc : LTE(b,c)): LTE(a,c)
Она гласит: если у нас есть доказательство ab утверждения LTE(a,b) (т.е., что A[a] <= A[b]) и доказательство bc утверждения LTE(b,c), то справедливо утверждение LTE(a,c), т.е. A[a] <= A[c]. lte_trans - функция, принимающая два факта-доказательства и возвращающая новый факт-доказательство. Ключевое слово praxi говорит, что это аксиома, и тела функции (конструктивного доказательства) не будет.
Имея утверждения об упорядоченности элементов, можно определить понятие отсортированности куска массива (по возрастанию). Кусок из единственного элемента всегда отсортирован, это тривиальный случай, служащий базой индукции. Если доказано, что кусок массива A[i..j] отсортирован, и доказано, что A[i-1] <= A[i], то учитывая транзитивность сравнения, кусок массива A[i-1 .. j] тоже отсортирован по возрастанию. Записывается это так:
//SORTED(i,j) means A[i..j] is sorted
dataprop SORTED(int, int) =
| {k:nat} SORTEDsingle(k,k)
| {i,j:nat | i > 0; i <= j} SORTEDjoin(i-1, j) of (LTE(i-1,i), SORTED(i,j))
Наша функция сортировки должна будет построить конструктивно доказательство утверждения SORTED(0, n-1). Поскольку мы не определили такое утверждение для пустых массивов, а только начиная с одного элемента, наша функция сортировки будет принимать только непустые массивы, что отражено в ее заголовке.
В процессе доказательства нам пригодится еще один вид утверждений: о том, что в некотором куске массива самый правый его элемент не меньше других (максимален), это то свойство, которым обладают правильные кучи Леонардо, а также правильный ряд куч. Устроено оно похожим образом. Для куска из одного элемента это свойство выполнено автоматически. А если у нас доказано, что среди элементов A[i..j] максимальный элемент самый правый, и что A[i-1] <= A[j], то и среди элементов A[i-1 .. j] тоже самый правый элемент максимальный.
// MAXRIGHT(i,j) means A[j] is the max of A[i..j]
dataprop MAXRIGHT(int, int) =
| {k:nat} MRsingle(k,k)
| {i,j:nat | i <= j; i > 0} MRgrow_l(i-1,j) of (LTE(i-1,j), MAXRIGHT(i,j))
Нам также пригодятся несколько простых вспомогательных теорем.
Во-первых, если среди элементов A[i..j] самый правый максимальный, то он не меньше любого из элементов A[i..j]. Для нас это очевидно, а компилятору нужно предъявить явное доказательство:
prfun lte_from_maxright {i,j,k:nat | i <= k; k <= j} ..
(mr: MAXRIGHT(i,j), k: int k, i: int i, j: int j): LTE(k,j) =
case+ mr of
| MRsingle () => LTErefl
| MRgrow_l(lte_ij, mr_i1j) =>
if k = i then lte_ij else lte_from_maxright(mr_i1j, k, i+1, j)
Ключевое слово prfun определяет рекурсивную функцию-доказательство, производящую факт-доказательство некоторого утверждения. В данном случае функция lte_from_maxright принимает доказательство mr утверждения MAXRIGHT(i,j), сами числа i и j, а также индекс k, заключенный между ними, и возвращает доказательство утверждения LTE(k,j), т.е. что A[k] <= A[j]. Тело функции-теоремы состоит из анализа случаев того, чем может быть mr. Паттерн-матчинг то бишь. Знак "+" после case означает обязательную проверку на exhaustiveness анализа, чтобы компилятор выдал ошибку, если мы какой-то возможный случай забыли рассмотреть. Фактически, доказательство MAXRIGHT(i,j) состоит из тривиального факта о j-том элементе и множестве фактов LTE(x,j). Перебирая их один за одним, мы найдем тот, где x будет равен k, это будет искомый факт. Ежели факт mr представлен вариантом MRsingle, то это тривиальный случай куска из единственного элемента, и мы можем применить рефлексивность нашего отношения и использовать LTErefl. Если же mr представлен вариантом MRgrow_l, т.е. построен из доказательств утверждений LTE(i,j) и MAXRIGHT(i+1, j), которые мы посредством паттерн-матчинга поименовали lte_ij и mr_i1j, то ежели k = i, то значит LTE(i,j) есть LTE(k,j), искомое утверждение, и имеющийся факт lte_ij его доказывает, его-то и вернем. А если i еще не равно k, то рекурсивно вызываем себя для mr_i1j : MAXRIGHT(i+1, j).
Рекурсивные функции-теоремы обязаны завершаться, ведь если такая функция зациклится, то нужное значение так и не найдет, и значит теорема не доказана. Поэтому тут требуется указать метрику завершимости - уменьшающееся при каждом рекурсивном вызове натуральное число. В данном случае это j - i, т.к. j не меняется, а i растет.
Функции-теоремы очень похожи на обычные функции, просто вместо данных там факты, а вместо их типов - утверждения, которые те доказывают. Однако главное отличие в том, что функции-теоремы используются только в момент компиляции, в конечный код они не попадают. Причем, они вообще никогда на самом деле не исполняются, им ведь главное типизироваться и не содержать ошибок. Если все варианты рассмотрены, и в каждом варианте все статические условия выполнены, то функция корректна, теорема доказана. Писать код, старательно доказывать компилятору его корректность, осознавая, что он все равно превратится в no-op, - не это ли благородное недеяние, воспетое древними мудрецами? Нет, не это. Но близко.
Еще одна теорема, которая нам пригодится. Если у двух подряд идущих кусков массивов максимальные элементы самые правые, и из этих двух локальных максимумов правый не меньше левого, то в силу транзитивности сравнения мы можем объединить два куска массива в один, и в нем тоже максимальный элемент будет самым правым. Записывается доказательство такой теоремы так:
prfn mr_join {a,b,c:nat | a <= b; b < c}
(ab: MAXRIGHT(a,b), bc: MAXRIGHT(b+1, c), lte_bc: LTE(b,c),
a: int a, b: int b): MAXRIGHT(a,c) = let
prfun loop {i:nat | i >= a; i <= b+1} .. (i: int i, mr_ic: MAXRIGHT(i,c)): MAXRIGHT(a,c) =
if i=a then mr_ic else
loop(i-1, MRgrow_l(lte_trans(lte_from_maxright(ab, i-1, a, b), lte_bc), mr_ic))
in
loop(b+1, bc)
end
Строится доказательство в цикле. Берем факт bc о том, что у правого куска (A[b+1..c]) самый правый элемент максимален, и по-одному элементу расширяем его влево: каждый очередной элемент из левого куска A[a..b] не больше A[b] (тут мы используем предыдущую теорему lte_from_maxright), а тот не больше, чем A[c] (это дано в условии в виде факта lte_bc: LTE(b,c) ), поэтому используя аксиому о транзитивности lte_trans получаем доказательство LTE(i-1, c), его прилепляем слева к текущему и получаем MAXRIGHT(i-1,c), пока не получим MAXRIGHT(a,c), который и требовалось получить.
Ну и еще одна теорема, простое следствие из предыдущей. Если в некотором куске массива A[a..b] самый правый элемент максимален, а следующий за ним элемент A[b+1] еще больше, то среди элементов A[a..b+1] самый правый максимальный.
prfn mr_grow_r {a,b:nat | a <= b}
(ab: MAXRIGHT(a,b), pf_lte: LTE(b,b+1), a: int a, b: int b): MAXRIGHT(a,b+1) = let
prval b1 : MAXRIGHT(b+1,b+1) = MRsingle
in
mr_join(ab, b1, pf_lte, a, b)
end
Ключевое слово prfn означает нерекурсивную функцию-теорему, для нее метрика завершимости не нужна. И так понятно, что она завершается, ибо внутри могут использоваться только завершающиеся функции-теоремы.
Акт 3. Структуры с гарантиями
Для реализации алгоритма нам потребуется хранить информацию о текущем устройстве ряда куч Леонардо в массиве. Некоторые реализации используют для этого битовый вектор, вычисляя необходимые параметры на ходу, но мы будем использовать более явную, наглядную и подробную структуру. Одна куча Леонардо у нас будет описываться структурой из трех чисел, ее характеризующих: индекс k, размер sz, равный L[k], и позиция корневого элемента в массиве, определяющая расположение кучи. Ряд куч будет описываться односвязным списком таких структур. Кроме данных структуры будут включать в себя факты об этих данных, это обеспечит корректность структур, ведь далеко не любая тройка чисел описывает правильную кучу Леонардо. Требуя предоставить доказательства, компилятор не даст нам создать неправильную структуру. Например, факт того, что sz=L[k], будет выражен явно доказательством утверждения LEON(k,sz). Само это утверждение определено так (мы это уже делали в прошлых сериях):
dataprop LEON(int, int) = //LEON(n,x) means L[n] = x
| {n:nat | n <= 1} LEONbase(n, 1)
| {n:nat | n > 1; a,b:nat | a > 0; b > 0} LEONind(n, a+b+1) of (LEON(n-2, a), LEON(n-1,b))
Кроме того, нам надо связать между собой значения root (позиция корневого элемента) и sz (размер кучи): root не может быть меньше, чем sz-1, а sz не может быть меньше 1. Опишем такое утверждение:
dataprop LH(int, int) = //LH(r,sz) means r >= sz - 1, r>=0, sz>=1
{r,sz:nat | sz >= 1; r >= sz - 1} LHpf(r,sz)
Задание предусловий перед конструктором не позволит его использовать, если условия не выполнены. Имея доказательство LHpf утверждения LH(r,sz), мы можем "извлечь" эти условия:
prfn lh_use {r,sz:int} (pf : LH(r, sz)): [r >= sz-1; sz >= 1] void =
case pf of LHpf () => ()
Здесь функция-теорема lh_use возвращает "ничто", void, снабженное несколькими статическими неравенствами. Тело ее состоит из "анализа вариантов": если передан такой-то конструктор, то его предусловия были выполнены, а значит они истинны и сейчас.
Итак, куча Леонардо, имеющая правильную форму, но для которой необязательно выполнено свойство кучи (про корень), будет описываться так:
typedef heap(r:int, k:int, sz:int) =
@{root = int r, k = int k, sz = int sz, pf_sz = LEON(k,sz), pf_r = LH(r,sz), pf_gc = GOODCHILDREN(k)}
Она состоит из трех целых чисел и доказательств некоторых утвеждений о них. Последнее из утверждений будет описано чуть позже.
Если для кучи выполнено ее свойство (корень не меньше корней подкуч), то корень ее является не только самым правым элементом, но и максимальным. Структуру, состоящую из кучи Леонардо и доказательства выполненности этого свойства, назвомем heap1:
typedef heap1(r:int, k:int, sz:int) =
@{ hp = heap(r,k,sz), pf_mr = MAXRIGHT(r-sz+1, r) }
Если для ряда куч выполнено свойство ряда (корни не убывают), то для каждой кучи в нем справедливо утверждение, что ее корень - самый правый и максимальный элемент всего ряда от начала до текущей кучи. Добавим в структуру доказательство такого факта, получим heap2:
typedef heap2(r:int, k:int, sz:int) =
@{ hp = heap(r,k,sz), pf_mr = MAXRIGHT(r-sz+1, r), pf_totalmr = MAXRIGHT(0,r) }
Именно из таких структур будет состоять список, определяющий правильный ряд куч Леонардо. Но в такой список нельзя добавлять что попало (например, один и тот же элемент), между позициями корней соседних элементов есть вполне определенная связь: они отличаются ровно на размер очередной кучи. Если m - общее число элементов в ряде куч, то ряд можно описать так:
datatype heaps(int) =
| heaps_nil (0)
| {m,r,k,sz:nat | m + sz - 1 == r} heaps_cons (r+1) of (heap2(r,k,sz), heaps(m))
#define :: heaps_cons
#define nil heaps_nil
В пустом ряду 0 элементов. Если есть ряд из m элементов и куча (со всеми свойствами) из sz элементов, то ее корень должен иметь быть на позиции m + sz - 1. Только если это условие выполнено, мы сможем добавить очередную кучу в наш ряд. Ряд куч представлен "списком", который синтаксически "растет" влево (как обычно это делают списки в функциональных языках), но логически в массиве ряд растет вправо: голова списка является последней, самой правой кучей.
Акт 4. Еще о числах Леонардо
В процессе работы нам понадобится уметь строить кучи Леонардо из двух меньших куч и нового корневого элемента, а также разбивать обратно большую кучу на две маленьких и корень. Позиции корней подкуч вычисляются через числа Леонардо, и чтобы компилятор был уверен, что мы не вылезем за пределы массива в ходе таких операций, нам понадобится ряд теорем.
Чтобы из двух куч и нового элемента сделать одну большую, нужно из доказательств о том, что размеры тех куч являются числами Леонардо, сделать доказательство, что размер новой тоже является нужным числом Леонардо. Для этого используется конструктор LEONind, но в его предусловиях требуется положительность значений. Ее можно извлечь из фактов-аргументов с помощью такой теоремы:
prfn leon_positive {n,x:nat} (pf : LEON(n,x)): [x > 0] void =
case+ pf of
| LEONbase () => ()
| LEONind(pf1, pf2) => ()
Вновь анализ вариантов и использование информации о соответствующих вариантам предусловиях. Выглядит функция-доказательство так, будто в ней ничего не делается, однако ж делается, просто за кадром. Еще забавнее это выглядит в следующей теореме:
prfun leon_isfun {n,x1,x2:nat} .. (pf1 : LEON(n,x1), pf2 : LEON(n,x2)): [x1==x2] void =
case+ (pf1, pf2) of
| (LEONbase (), LEONbase ()) => ()
| (LEONind(p1a,p1b), LEONind(p2a,p2b)) => let
prval () = leon_isfun(p1a, p2a)
prval () = leon_isfun(p1b, p2b)
in () end
Тут мы доказываем, что L[k] - функция в математическом смысле, т.е. Если x=y, то L[x]=L[y]. Теорема получает два факта (LEON(n,x1) и LEON(n,x2)) и доказывает, что x1==x2. Опять разбор вариантов и сопоставление аргументов. Если оба факта - LEONbase, то имеют "тип" LEON(n,1), т.е. x1=1 и x2=1, а значит x1==x2. Если оба - LEONind, то содержат вполне определенные доказательства, которые можно сопоставить друг с другом рекурсивно. А разные конструкторы pf1 и pf2 иметь не могут, т.к. у разных конструкторов взаимоисключающие предусловия на n, так что нерассмотренных вариантов в case+ не возникает, и компилируется такое доказательство без ошибок. Используется оно в теореме о монотонности L[x]:
prfn leon_mono {k1,sz1,sz2:nat | k1 > 0}
(pf1 : LEON(k1, sz1), pf2 : LEON(k1 + 1,sz2)): [sz1 < sz2-1] void = let
prval LEONind(pf2_2, pf2_1) = pf2
prval () = leon_isfun(pf1, pf2_1)
in () end
Тут доказывается, что после единицы каждое следующее число Леонардо больше предыдущего (как минимум на 2). Что тут происходит: В предусловии сказано, что k1 > 0, значит k1 + 1 > 1, значит pf2 имеет вид LEONind(...), и паттерн-матчингом в первой строке мы извлекаем входящие в него доказательства, которые назовем pf2_2 и pf2_1. Если вспомнить определение LEONind, видно, что они имеют "тип" LEON(k1 + 1 - 2, x1) и LEON(k1 + 1 - 1, x2) соответственно, где x1 и x2 - некоторые натуральный числа. Получается, что у pf2_1 и исходного аргумента pf1 похожий "тип" - они оба LEON(k1, ...), т.е. утверждения о числе L[k1]. Теперь мы задействуем теорему leon_isfun, которая устанавливает равенство значений L[k1], т.е. sz1==x2. Но из определения LEON(k1 + 1,sz2) компилятор знает, что sz2 = x1 + x2 + 1, а значит sz2 = x1 + sz1 + 1, где x1 - некоторое натуральное число, а значит sz1 < sz2-1, ч.т.д.
Еще одна похожая теорема: если для натуральных чисел k,sz, sz1 и sz2, таких что k > 1 и sz2 == sz - 1 - sz1, у нас есть доказательство, что L[k]=sz, а L[k-1]=sz1, то L[k-2]=sz2. Это нужно при вычислении размеров подкуч: если мы знаем размер большой кучи L[k] и вычислили размер одной из подкуч L[k-1], то размер второй подкучи L[k-2] можем получить вычитанием.
prfn leon_size_dif {k,sz, sz1, sz2 : nat | k > 1; sz2 == sz - 1 - sz1}
(pfsz : LEON(k,sz), pfsz1 : LEON(k-1,sz1)) : LEON(k-2, sz2) =
case+ pfsz of
| LEONind(pf_2, pf_1) => let prval () = leon_isfun(pf_1, pfsz1) in pf_2 end
Способ доказательства практически идентичен предыдущей теореме.
Ну и еще одна мелочь, которая потребуется в коде: доказательство того, что для k < 2 L[k]=1.
prfn leon_base_is1 {k,sz:nat | k < 2} (pf : LEON(k,sz)): [sz==1] void =
case+ pf of LEONbase () => ()
Анализ вариантов исчерпывается единственным случаем в силу условия на k, и из определения LEONbase компилятор извлекает требуемый факт.
Продолжение...