я вижу квантовые операторы
Сегодня и вы их увидите. Сначала нарисуем вещественную прямую и возьмем какую-нибудь простую вещественную функцию, которая каждой точке вещественной прямой x сопоставляет некоторое вещественное число y, можем эти x и y использовать в качестве координат точек на плоскости и нарисовать график:

А теперь возьмем функцию f, которая возвращает не вещественное число, а комплексное. Это пара вещественных чисел (Re,Im), и их можно тоже использовать в качестве координат, надо только добавить еще одно измерение. (x,y,z) = (x, Re (f x), Im (f x))

У нас по-прежнему есть вещественная прямая, и через каждую ее точку проходит перпендикулярная ей комплексная плоскость, на которой можно точками или векторами рисовать комплексные числа. Этого достаточно, чтобы изобразить одномерную волновую функцию из квантовой механики.
Краткое отступление-вступление. Мы будем рассматривать квантовую механику в ее самом простом варианте, без релятивизма, без вторичного квантования и всего такого. Это очень геометричная, легко визуально представимая штука. Квантовое состояние это вектор в некотором пространстве. Вектора можно складывать, можно умножать на комплексное число, получается другой вектор. Для пар векторов в этом пространстве можно вычислять их скалярное произведение и получать комплексное число, соответствующее длине проекции одного на другого. Если проекция нулевая, вектора ортогональны. Через проекцию вектора на себя можно узнать его длину. Набор ортогональных единичных векторов, на линейную комбинацию которых можно разложить произвольный вектор, называется базисом. Таких наборов-базисов много, можно выбирать любой. Штуковина/аппарат/машина, которая берет вектор и превращает/отображает его в другой вектор, называется оператором. Если мы засунули какой-то вектор v в эту машину, а на выходе получили его же, только отмасштабированным, k*v (где k - комплексное число), то такой вектор называется собственным вектором данного оператора, а это число k - собственным значением. У некоторых операторов все собственные значения оказываются вещественными числами, и постулируется, что результаты физических измерений это такие собственные значения таких вот замечательных операторов, каждой физически наблюдаемой величине соответствует свой оператор. Например, в нашей одномерной квантовой механике есть оператор координаты x, его собственные значения заполняют собой всю вещественную прямую, т.е. каждое вещественное число это отдельное собственное значение оператора координаты, и ему соответствует свой собственный вектор - состояние, когда частица имеет в точности эту координату и никакую другую. Обычно же вектор состояния можно проецировать на всевозможные собственные вектора координаты и получать какие-то коэффициенты, это и есть комплексные значения f(x), той функции, что мы тут рисуем. Если для разных x получаются отличные от нуля значения f(x), значит наша система находится в суперпозиции всех этих состояний с определенной координатой, и f(x) нам дает вес каждого такого конкретного состояния для каждого x. Этот вес также называется амплитудой вероятности. Это комплексное число, и квадрат его модуля соответствует (плотности) вероятности найти частицу в этом состоянии (в данном случае в этой координате). Модуль амплитуды можно нарисовать отдельно сереньким, выглядеть это может так:

Как меняется ф-я f при движении от x к x+dx? f(x+dx) - f(x), это тоже комплексное число. Возьмем предел при dx -> 0, получим какое-то значение для каждого x, новую функию - первую производную f по x.

Если поведение физической системы не зависит явным образом от координаты, а, например, только от взаимного расположения частиц и их скоростей, т.е. ничего не изменится, если немножко сдвинуть систему в сторону или просто передвинуть начало координат, систему отсчета, то говорят, что система обладает пространственной трансляционной симметрией. Каждая симметрия, каждое такое преобразование координат, не меняющее поведения, автоматически дает нам какую-то сохраняющуюся величину, спасибо теореме Нётер, теории групп и матану. Для трансляционной симметрии в пространстве это сохранение момента импульса (momentum), для аналогичной симметрии при сдвиге во времени - сохранение энергии. В квантах этим величинам соответствуют операторы, и оператор импульса, связанный со сдвигом в пространстве, ожидаемо оказывается связанным с производной по координате. Это она и есть, с точностью до мнимой константы (которая нужна, чтобы собственные значения были вещественными).
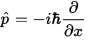
А значит мы уже можем его нарисовать, вернее результат его действия на волновую функцию. Надо лишь вычислить производную по х и умножить на -ih. Единицы измерения мы можем выбрать такие, что h=1, поэтому надо лишь умножить на -i, что эквивалентно повороту комплексного числа на 90 градусов. Так, если взять простую синусоиду, ее производная это косинус (синий), и импульс будет поворотом производной на пипополам:

Для более сложной и неплоской ф-ии получается более интересная картинка:

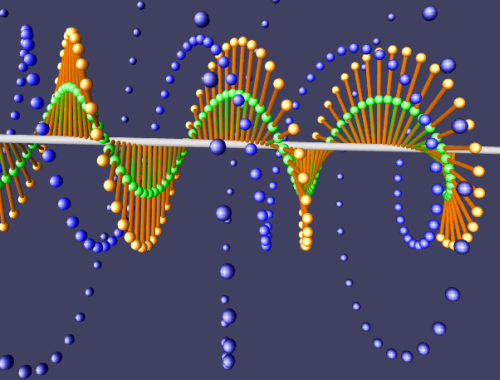
Что интересно, если f(x) = e^(ix), т.е. обе координаты варьируются как синус и косинус, вырисовывая спираль единичного радиуса в пространстве, то первая производная перпендикулярна исходной ф-ии, а умножение на -i поворачивает ее обратно, в результате оператор импульса для данной ф-ии возвращает ее же (ну или умноженную на постоянную Планка h в другой системе единиц).

А это значит, что такая вот спиралька - это собственный вектор оператора импульса. Т.е. вот так выглядит волновая функция частицы, для которой импульс имеет одно четко определенное значение. Заметьте, что амплитуда этой волновой ф-ии везде одинакова, т.е. вероятность найти частицу одинакова для всех точек пространства. Это прямая иллюстрация принципа неопределенности Гейзенберга: если знаешь импульс, то ваще не знаешь координату. Что будет, если взять не просто e^(ix), a e^(ikx)? Чем больше k, тем быстрее/сильнее спиралька будет закручиваться, тем больше будет первая производная, больше импульс. Разным конкретным значениям импульса соответствуют просто разные такие вот спиральки, и их можно использовать в качестве базиса, разложить произвольную функцию на взвешенную сумму таких спиралек.
Если можем найти первую производную, то можем найти и вторую. Раз уж речь ведем о частице с импульсом, то найдем и ее кинетическую энергию: p = mv, p2 = m2*v2, E = mv2/2 = p*p / 2m.
На языке операторов это значит надо применить оператор p дважды и разделить на 2m.
Каждое применение оператора импулься это взятие производной и умножение на -ih, и (-ih)*(-ih) = -h2, получаем
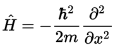
Например, для синусоиды, если первая производная это косинус (синий), вторая производная это минус синус (темно синий), и энергия получается ее умножением на отрицательную вещественную константу, нарисуем желтым:

Что занятно, тут на выходе оператора энергии опять получили слегка отмасштабированную исходную функцию, т.е. такая плоская синусоида - это собственный вектор данного оператора.
А если опять взять ф-ю Эйлера, спиральку, то и там тоже: первая производная там это просто поворот на пипополам, вторая еще на пипополам, а энергия берет ее с минусом, получаем исходную ф-ю, с точностью до константы.

Опять же, чем быстрее закручивается спиралька (больше k в e^(ikx)), тем больше первая и вторая прозводные, тем больше энергия. При другой частоте k оператор энергии все еще дает отмасштабированную исходную ф-ию, только коэффициент масштабирования получается другой, другое собственное значение энергии.
Что интересно, если взять k отрицательным, то спиралька закручивается в другую сторону, и импульс оказывается отрицательным (на выходе оператора импульса исходная ф-я, умноженная на отрицательную константу), а энергия все равно положительной. Что соответствует движению частицы в другую сторону. Кстати!
До этого момента ни о каком движении речи не шло, у нас х это пространственная координата, время никак не фигурировало. В реальности же частицы как-то движутся, системы эволюционируют. По-хорошему, нам нужна функция f(x,t), просто пока мы ее рассматривали для фиксированного значения t. По идее, наша волновая ф-я описывает полное состояние системы. Значит ли это, что зная его, мы можем рассчитать ее состояние в следующий момент времени? Да фиг. Разве можно, зная f(x,t0), узнать f(x, t) для произвольного t? Нужна какая-то дополнительная информация. Для каждого значения t, f(x,t) - это своя ф-я от х, выражение вектора квантового состояния. В другой момент времени будет уже другое состояние, другой вектор. Можно для каждого значения t представить аппарат, который берет вектор начального состояния и возвращает вектор состояния в момент t. Это оператор эволюции U(t). Для нулевой разницы во времени он должен возвращать начальное состояние, для небольшого шага - небольшое изменение, плавное. Т.е. U(t) = 1 + G(t), где G(t) - что-то малое при малых t. Выразив через них f(x, t + dt) - f(x, t) и устремив dt к 0, получим выражение для производной f по времени, где справа будет некоторый оператор. Вынеся из него комплексную константу, можно его сделать эрмитовым, имеющим вещественные собственные значения и ведущим себя как физически наблюдаемая величина. Получим уравнение Шрёдингера
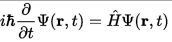
Наложим требования сохранения ортогональных (физически различимых) состояний и прочие физ. соображения, пропустим кусок логики про связь симметрии сдвига во времени, сохранения энергии и оператора энергии, и получим, что соответствующий производной по времени квантовый оператор - это оператор энергии, точнее гамильтониан. Для свободной частицы мы его уже вычислили и нарисовали выше. Чтобы вычислить производную волновой ф-ии по времени, надо лишь разделить его на ih, что означает опять масштабирование и поворот в комлексной плоскости на пипополам (нарисуем красным):
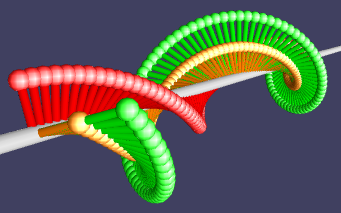
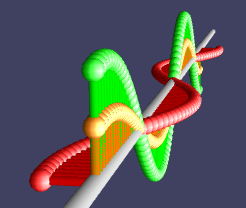
Производная по времени это скорость, это вектор, указывающий направление движения. Если отложим его от самих точек, то увидим, куда будет двигаться ф-я:

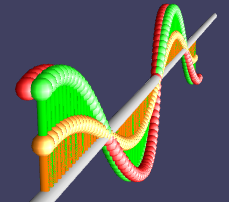
Для таких вот ф-ий это означает очень простое движение: вращение в комплексной плоскости.
Но для других состояний, например более-менее локализованных частиц, это не только вращение, но и движение радиальное, т.е. амплитуда вероятности может расти в одних местах и уменьшаться в других:
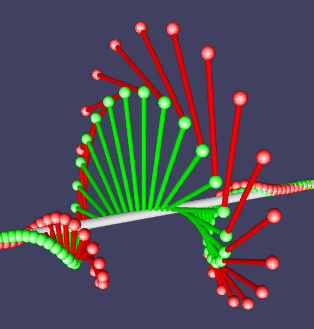
А значит такая частица будет со временем двигаться в пространстве. Проинтегрируем это хозяйство во времени и вуаля!
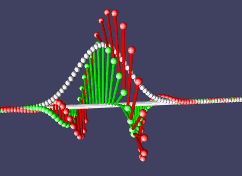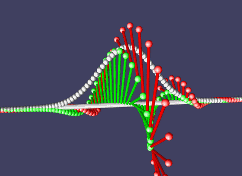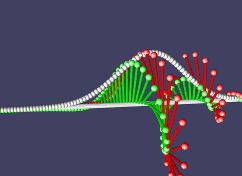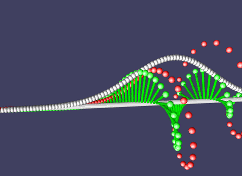
Наша частица движется и потихоньку расплывается в пространстве. Причем направление движения зависит от того, в какую сторону она закручена в комплексном пространстве.
Теперь, поскольку именно и только гамильтониан определяет производную по времени, а она нам дает всю эволюцию системы во времени, значения f(x,t) для всех будущих t, то получается, что все отличие свободной частицы от частицы, испытывающей какие-то внешние воздействия, силы, это отличие в форме оператора энергии. Так, мы можем добавить в него член, зависящий лишь от координаты, функцию потенциала. Это нам даст потенциальную энергию, а частица вдруг зашевелится по-другому. В классической механике сила это минус производная от потенциала, благодаря чему частицы стремятся уменьшить свою потенциальную энергию. Если добавить линейный потенциал V(x) = k*x, это будет означать постоянно действующую силу. Для положительного k это значит, что потенциальная энергия растет при увеличении х, значит сила направлена влево, в сторону уменьшения потенциала. Проверим:
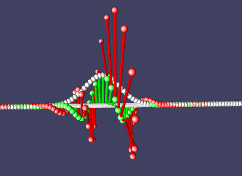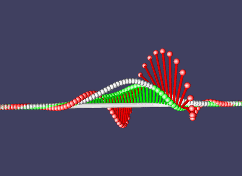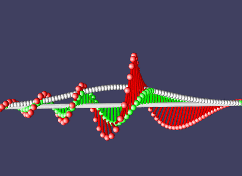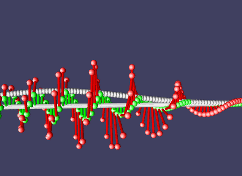
Двигавшаяся вправо частица затормозила, развернулась и стала двигаться влево. Вот оно, пробуждение силы!
При нулевом и линейном потенциале частица продолжает расплываться от своего центра, неопределенность координаты растет со временем. Теперь посмотрим на obligatory example, гармонический осциллятор. Всего-то надо задать потенциал как V(x) = k*x2. Это создает силу, направленную к центру координат, и линейно растущую по мере удаления от центра. Подобно шарику на пружинке. Статические решения тут не так интересны, а интересно посмотреть, как частицы двигаются в таком потенциале:

Как и можно было ожидать, частица болтается туда-сюда, как и велит ей сила. Что интересно, расплывания больше не происходит, получается такой периодический процесс с сохранением степени локализации частицы.
А теперь десерт. Этот пост инспирирован (а идея визуализации сперта) вот этим замечательным роликом. Увидев его, мне захотелось самому пощупать такую 3D визуализацию и позапускать разные численные эксперименты. И тогда я сделал такой вот интерактивный playground, в котором и были сделаны картинки и гифки из поста, и теперь вы тоже можете поиграться с разными функциями и операторами, слава WebGL! Там можно мышой хватать и крутить в разные стороны. Играться можно прямо в браузере здесь:
http://data.infognition.com/wavefun/
Там численное интегрирование на ограниченном отрезке, и если ф-я заметно отлична от нуля на концах отрезка (как те спиральки и синусоиды), то из-за дурацких значений производных на концах возникают всякие смешные эффекты, через некоторое время от концов к середине приходит кракен и все портит.
Написано все на Elm'e, исходники здесь:
https://bitbucket.org/thedeemon/wavefun/
Про свежие впечатления от последнего Elm'a (там опять все переделали) напишу отдельно.

А теперь возьмем функцию f, которая возвращает не вещественное число, а комплексное. Это пара вещественных чисел (Re,Im), и их можно тоже использовать в качестве координат, надо только добавить еще одно измерение. (x,y,z) = (x, Re (f x), Im (f x))

У нас по-прежнему есть вещественная прямая, и через каждую ее точку проходит перпендикулярная ей комплексная плоскость, на которой можно точками или векторами рисовать комплексные числа. Этого достаточно, чтобы изобразить одномерную волновую функцию из квантовой механики.
Краткое отступление-вступление. Мы будем рассматривать квантовую механику в ее самом простом варианте, без релятивизма, без вторичного квантования и всего такого. Это очень геометричная, легко визуально представимая штука. Квантовое состояние это вектор в некотором пространстве. Вектора можно складывать, можно умножать на комплексное число, получается другой вектор. Для пар векторов в этом пространстве можно вычислять их скалярное произведение и получать комплексное число, соответствующее длине проекции одного на другого. Если проекция нулевая, вектора ортогональны. Через проекцию вектора на себя можно узнать его длину. Набор ортогональных единичных векторов, на линейную комбинацию которых можно разложить произвольный вектор, называется базисом. Таких наборов-базисов много, можно выбирать любой. Штуковина/аппарат/машина, которая берет вектор и превращает/отображает его в другой вектор, называется оператором. Если мы засунули какой-то вектор v в эту машину, а на выходе получили его же, только отмасштабированным, k*v (где k - комплексное число), то такой вектор называется собственным вектором данного оператора, а это число k - собственным значением. У некоторых операторов все собственные значения оказываются вещественными числами, и постулируется, что результаты физических измерений это такие собственные значения таких вот замечательных операторов, каждой физически наблюдаемой величине соответствует свой оператор. Например, в нашей одномерной квантовой механике есть оператор координаты x, его собственные значения заполняют собой всю вещественную прямую, т.е. каждое вещественное число это отдельное собственное значение оператора координаты, и ему соответствует свой собственный вектор - состояние, когда частица имеет в точности эту координату и никакую другую. Обычно же вектор состояния можно проецировать на всевозможные собственные вектора координаты и получать какие-то коэффициенты, это и есть комплексные значения f(x), той функции, что мы тут рисуем. Если для разных x получаются отличные от нуля значения f(x), значит наша система находится в суперпозиции всех этих состояний с определенной координатой, и f(x) нам дает вес каждого такого конкретного состояния для каждого x. Этот вес также называется амплитудой вероятности. Это комплексное число, и квадрат его модуля соответствует (плотности) вероятности найти частицу в этом состоянии (в данном случае в этой координате). Модуль амплитуды можно нарисовать отдельно сереньким, выглядеть это может так:

Как меняется ф-я f при движении от x к x+dx? f(x+dx) - f(x), это тоже комплексное число. Возьмем предел при dx -> 0, получим какое-то значение для каждого x, новую функию - первую производную f по x.

Если поведение физической системы не зависит явным образом от координаты, а, например, только от взаимного расположения частиц и их скоростей, т.е. ничего не изменится, если немножко сдвинуть систему в сторону или просто передвинуть начало координат, систему отсчета, то говорят, что система обладает пространственной трансляционной симметрией. Каждая симметрия, каждое такое преобразование координат, не меняющее поведения, автоматически дает нам какую-то сохраняющуюся величину, спасибо теореме Нётер, теории групп и матану. Для трансляционной симметрии в пространстве это сохранение момента импульса (momentum), для аналогичной симметрии при сдвиге во времени - сохранение энергии. В квантах этим величинам соответствуют операторы, и оператор импульса, связанный со сдвигом в пространстве, ожидаемо оказывается связанным с производной по координате. Это она и есть, с точностью до мнимой константы (которая нужна, чтобы собственные значения были вещественными).
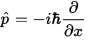
А значит мы уже можем его нарисовать, вернее результат его действия на волновую функцию. Надо лишь вычислить производную по х и умножить на -ih. Единицы измерения мы можем выбрать такие, что h=1, поэтому надо лишь умножить на -i, что эквивалентно повороту комплексного числа на 90 градусов. Так, если взять простую синусоиду, ее производная это косинус (синий), и импульс будет поворотом производной на пипополам:

Для более сложной и неплоской ф-ии получается более интересная картинка:

Что интересно, если f(x) = e^(ix), т.е. обе координаты варьируются как синус и косинус, вырисовывая спираль единичного радиуса в пространстве, то первая производная перпендикулярна исходной ф-ии, а умножение на -i поворачивает ее обратно, в результате оператор импульса для данной ф-ии возвращает ее же (ну или умноженную на постоянную Планка h в другой системе единиц).

А это значит, что такая вот спиралька - это собственный вектор оператора импульса. Т.е. вот так выглядит волновая функция частицы, для которой импульс имеет одно четко определенное значение. Заметьте, что амплитуда этой волновой ф-ии везде одинакова, т.е. вероятность найти частицу одинакова для всех точек пространства. Это прямая иллюстрация принципа неопределенности Гейзенберга: если знаешь импульс, то ваще не знаешь координату. Что будет, если взять не просто e^(ix), a e^(ikx)? Чем больше k, тем быстрее/сильнее спиралька будет закручиваться, тем больше будет первая производная, больше импульс. Разным конкретным значениям импульса соответствуют просто разные такие вот спиральки, и их можно использовать в качестве базиса, разложить произвольную функцию на взвешенную сумму таких спиралек.
Если можем найти первую производную, то можем найти и вторую. Раз уж речь ведем о частице с импульсом, то найдем и ее кинетическую энергию: p = mv, p2 = m2*v2, E = mv2/2 = p*p / 2m.
На языке операторов это значит надо применить оператор p дважды и разделить на 2m.
Каждое применение оператора импулься это взятие производной и умножение на -ih, и (-ih)*(-ih) = -h2, получаем
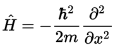
Например, для синусоиды, если первая производная это косинус (синий), вторая производная это минус синус (темно синий), и энергия получается ее умножением на отрицательную вещественную константу, нарисуем желтым:

Что занятно, тут на выходе оператора энергии опять получили слегка отмасштабированную исходную функцию, т.е. такая плоская синусоида - это собственный вектор данного оператора.
А если опять взять ф-ю Эйлера, спиральку, то и там тоже: первая производная там это просто поворот на пипополам, вторая еще на пипополам, а энергия берет ее с минусом, получаем исходную ф-ю, с точностью до константы.

Опять же, чем быстрее закручивается спиралька (больше k в e^(ikx)), тем больше первая и вторая прозводные, тем больше энергия. При другой частоте k оператор энергии все еще дает отмасштабированную исходную ф-ию, только коэффициент масштабирования получается другой, другое собственное значение энергии.

Что интересно, если взять k отрицательным, то спиралька закручивается в другую сторону, и импульс оказывается отрицательным (на выходе оператора импульса исходная ф-я, умноженная на отрицательную константу), а энергия все равно положительной. Что соответствует движению частицы в другую сторону. Кстати!
До этого момента ни о каком движении речи не шло, у нас х это пространственная координата, время никак не фигурировало. В реальности же частицы как-то движутся, системы эволюционируют. По-хорошему, нам нужна функция f(x,t), просто пока мы ее рассматривали для фиксированного значения t. По идее, наша волновая ф-я описывает полное состояние системы. Значит ли это, что зная его, мы можем рассчитать ее состояние в следующий момент времени? Да фиг. Разве можно, зная f(x,t0), узнать f(x, t) для произвольного t? Нужна какая-то дополнительная информация. Для каждого значения t, f(x,t) - это своя ф-я от х, выражение вектора квантового состояния. В другой момент времени будет уже другое состояние, другой вектор. Можно для каждого значения t представить аппарат, который берет вектор начального состояния и возвращает вектор состояния в момент t. Это оператор эволюции U(t). Для нулевой разницы во времени он должен возвращать начальное состояние, для небольшого шага - небольшое изменение, плавное. Т.е. U(t) = 1 + G(t), где G(t) - что-то малое при малых t. Выразив через них f(x, t + dt) - f(x, t) и устремив dt к 0, получим выражение для производной f по времени, где справа будет некоторый оператор. Вынеся из него комплексную константу, можно его сделать эрмитовым, имеющим вещественные собственные значения и ведущим себя как физически наблюдаемая величина. Получим уравнение Шрёдингера
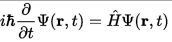
Наложим требования сохранения ортогональных (физически различимых) состояний и прочие физ. соображения, пропустим кусок логики про связь симметрии сдвига во времени, сохранения энергии и оператора энергии, и получим, что соответствующий производной по времени квантовый оператор - это оператор энергии, точнее гамильтониан. Для свободной частицы мы его уже вычислили и нарисовали выше. Чтобы вычислить производную волновой ф-ии по времени, надо лишь разделить его на ih, что означает опять масштабирование и поворот в комлексной плоскости на пипополам (нарисуем красным):


Производная по времени это скорость, это вектор, указывающий направление движения. Если отложим его от самих точек, то увидим, куда будет двигаться ф-я:


Для таких вот ф-ий это означает очень простое движение: вращение в комплексной плоскости.
Но для других состояний, например более-менее локализованных частиц, это не только вращение, но и движение радиальное, т.е. амплитуда вероятности может расти в одних местах и уменьшаться в других:

А значит такая частица будет со временем двигаться в пространстве. Проинтегрируем это хозяйство во времени и вуаля!

Наша частица движется и потихоньку расплывается в пространстве. Причем направление движения зависит от того, в какую сторону она закручена в комплексном пространстве.
Теперь, поскольку именно и только гамильтониан определяет производную по времени, а она нам дает всю эволюцию системы во времени, значения f(x,t) для всех будущих t, то получается, что все отличие свободной частицы от частицы, испытывающей какие-то внешние воздействия, силы, это отличие в форме оператора энергии. Так, мы можем добавить в него член, зависящий лишь от координаты, функцию потенциала. Это нам даст потенциальную энергию, а частица вдруг зашевелится по-другому. В классической механике сила это минус производная от потенциала, благодаря чему частицы стремятся уменьшить свою потенциальную энергию. Если добавить линейный потенциал V(x) = k*x, это будет означать постоянно действующую силу. Для положительного k это значит, что потенциальная энергия растет при увеличении х, значит сила направлена влево, в сторону уменьшения потенциала. Проверим:

Двигавшаяся вправо частица затормозила, развернулась и стала двигаться влево. Вот оно, пробуждение силы!
При нулевом и линейном потенциале частица продолжает расплываться от своего центра, неопределенность координаты растет со временем. Теперь посмотрим на obligatory example, гармонический осциллятор. Всего-то надо задать потенциал как V(x) = k*x2. Это создает силу, направленную к центру координат, и линейно растущую по мере удаления от центра. Подобно шарику на пружинке. Статические решения тут не так интересны, а интересно посмотреть, как частицы двигаются в таком потенциале:

Как и можно было ожидать, частица болтается туда-сюда, как и велит ей сила. Что интересно, расплывания больше не происходит, получается такой периодический процесс с сохранением степени локализации частицы.
А теперь десерт. Этот пост инспирирован (а идея визуализации сперта) вот этим замечательным роликом. Увидев его, мне захотелось самому пощупать такую 3D визуализацию и позапускать разные численные эксперименты. И тогда я сделал такой вот интерактивный playground, в котором и были сделаны картинки и гифки из поста, и теперь вы тоже можете поиграться с разными функциями и операторами, слава WebGL! Там можно мышой хватать и крутить в разные стороны. Играться можно прямо в браузере здесь:
http://data.infognition.com/wavefun/
Там численное интегрирование на ограниченном отрезке, и если ф-я заметно отлична от нуля на концах отрезка (как те спиральки и синусоиды), то из-за дурацких значений производных на концах возникают всякие смешные эффекты, через некоторое время от концов к середине приходит кракен и все портит.
Написано все на Elm'e, исходники здесь:
https://bitbucket.org/thedeemon/wavefun/
Про свежие впечатления от последнего Elm'a (там опять все переделали) напишу отдельно.