ФРАКТАЛЬНО-ГОЛОГРАФИЧЕСКИЙ КОНСТРУКТ

tmuna yafa by (c) yosi vaknin '21
"..процессы, отражающие фрактальное самоподобие, основаны, прежде всего, на принципе обратной связи, когда результат одной итерации является начальным значением следующей итерации. Наряду с этим, фрактальная геометрия позволяет устанавливать взаимозависимость между геометриями в различных масштабах, а именно, понимать, как микроскопическое поведение тех или иных систем связано с тем, что можно наблюдать в макроскопическом масштабе (Mandelbrot 1980; 1982). Многообразие фракталов при этом, содержащих множество виртуальных наборов всех возможностей, отраженное через принцип самоподобия, описывается довольно простой математической формулой вида: Zn+1 = Z2n + C . Данная формула получила название множества Мандельброта (ММ). В ней, как мы отметили выше, отражен процесс повторения процедуры неопределенное число раз (процесс итерации), фиксируя этим непрерывное изменение и самоизменение опосредованного операцией непрерывного самоотнесения (самореферентности). Процессу итерации, отраженному в данной формуле, соответствуют как золотая пропорция (ЗП), выступающая прообразом рядов (чисел) Фибоначчи (РФ), так и разного вида геометрические и алгебраические прогрессии. Широкие исследования в области фрактальной геометрии и синергетики выявили глубокую связь между этими научными направлениями (Шелепин, 2001). Так, например, математический язык фракталов точно и корректно описывает тонкую структуру странных (фрактальных) аттракторов.
Важный аспект фрактальной геометрии заключается в том, что она содержит в себе, в рамках диалектического принципа, эффекты синергии, т.е. «кооперативные», синтетические взаимоотношения динамичности и статистичности (Богатых, 2006; 2012). Динамичность системы - это фундаментальное качество развития системы как целого, так как именно оно связано с однозначной предсказуемостью, детерминированностью развития тех или иных систем и процессов между точками выбора путей эволюции (точки бифуркации). Статистичность (стохастичность, случайность, т.е. сами точки бифуркации) - фундаментальное качество системы, относится к уровню ее элементного строения, на котором будут возникать различного рода мутации, кардинально преобразуя систему. Важно отметить, что, когда система попадает в точку бифуркации, ее поведение в ней зависит от предыдущей истории системы, оно уникально для данной системы. Иными словами, в данной реальности, которой внутренне присуща динамичность и статистичность, просматривается синтез позитивных элементов детерминистической и вероятностной картин мира, отражая собой в этом специфическом единстве противоположностей саморазвитие органического мира
Фрактальная размерность
Само понятие размерности фрактального множества Б. Мандельброт предложил применять с целью количественного описания фрактальных множеств. В более общей форме Мандельброт предлагает следующее определение фрактала: «Фракталом называется множество, размерность Хаусдорфа-Безиковича для которого строго больше его топологической размерности» (Мандельброт, 2002). Данное определение, в свою очередь, требует определений терминов: «размерность Хаусдорфа-Безиковича», т.е. дробная (фрактальная) размерность (D), и «топологическая размерность» (Dт), которая всегда равна целому числу. В обыденном понимании размерность геометрического множества (фрактальный рост) представляет собой число измерений, с помощью которых можно задать положение точки на геометрическом объекте. И все же смысл понятия «размерность» значительно шире, так как оно отражает более «тонкие» топологические свойства объектов, совпадая при этом с числом независимых переменных, необходимых для описания объекта только в частных случаях. Так, распространение данного представления на множество Кантора даст уже дробную размерность: dCantor = 0.63. Размерность кривой Коха: dKokh = 1.261. Рассмотренные объекты, как и ряд других объектов: кривая Пеано, ковер Серпинского и т.д. демонстрируют фундаментальное свойство фрактальных объектов, их самоподобие, являющееся общим для всех фракталов (Mandelbrot, 1982; Кроновер, 2000).
Голография
Как известно, голография представляет собой трехмерную, безлинзовую фотографию, и способна воспроизводить объемные реалистичные образы материальных объектов. Математические основы голографической техники были разработаны Денисом Габором еще в конце 40-х годов ХХ-го века. Сами голограммы выражаются при этом в форме так называемых преобразований Фурье, в основе которых - любой самый сложный паттерн может быть разложен на ряд регулярных волн. Обратное преобразование Фурье, как и ряд других сходных с ними преобразований, при наличии правил трансформации превращает голографическую сферу в структурированную. Иными словами, переводит волновой паттерн снова в изображение. Здесь не в последнюю очередь срабатывает особое свойство голограммы, а именно, тот факт, что каждая часть голограммы, отражающая целое, обусловлена частностями математического преобразования картины или паттерна в язык волновых форм. Именно данные преобразования позволили Д. Габору перевести изображение объекта в интерференционное «пятно» на голографической пленке и изобрести способ обратного преобразования интерференционных паттернов в первоначальное изображение.
Самоподобные структуры в голографии
Важнейшим физическим принципом, лежащим в основе голографии, является принцип Гюйгенса-Френеля. Суть его в том, что каждая точка фронта волны, исходящей из какого-либо источника света (рис. 1, А), представляет собой центр вторичного возмущения. Этот центр, в свою очередь, вызывает элементарные сферические волны (рис. 1, В), а волновой фронт в более поздние моменты времени становится огибающим эти волны (рис. 1, С). Если продолжить умозрительно эту цепочку дальше, то получим, что каждый фронт второго порядка создает источники и фронты третьего, четвертого порядка (рис. 2) и т.д. Видно, что при таком распространении волны получается своеобразная самоподобная структура, где каждый «источник» n-го порядка подобен всем источникам «предыдущих» порядков, и каждый фрагмент волны подобен всей волне.
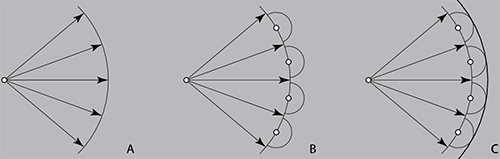
Рис. 1. Распространение волнового фронта. А. Фронт первичной волны. В. Вторичные источники элементарных волн. С. Огибающая вторичных источников, совпадающая с первоначальным фронтом.
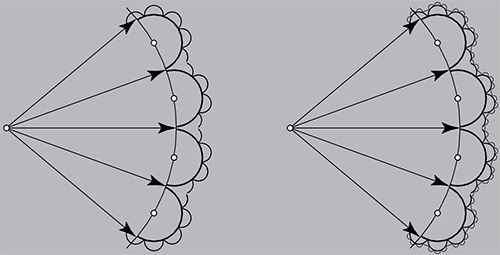
Рис. 2. Фронты третьего и четвертого порядков.
Иными словами, наличествует самоподобный конструкт - скейлинг или масштабная инвариантность. Аналогичное свойство масштабной инвариантности сохраняет и голографическая пленка и, как следствие, любой фрагмент пленки способен восстановить весь исходный образ. Учитывая, что принцип Гюйгенса- Френеля в оптической голографии играет основополагающую роль, можно предположить, что, моделируя, например, символьное рассеивание информации, можно также столкнуться с проявлениями самоподобия.
Голограммы обладают также уникальной способностью к хранению информации. Например, голографическая пленка может содержать более сотни изображений на одной и той же поверхности. Таким образом, на каждую точку голограммы фактически проецируется сразу весь образ, обеспечивая многократно повторенную, избыточную информацию. Данная колоссальная избыточность голографической записи обеспечивает высокую помехоустойчивость и надежность хранения информации.
Фрактально-голографический конструкт
В целом фракталы являются близким структурным описанием голограммы, позволяя тем самым обозначать данное образование как фрактально-голографический конструкт. При этом оба конструкта - фрактальность и голография - имеют дело с законами, уточняющими отношения между элементами или системами, образующими организацию фрактально-голографического конструкта. Структура данной организации становится более организованной при нарастании большого количества степеней свободы, обеспечивая этим перекрывание элементов, входящих в систему при максимально возможных отношениях элементов. Данная особенность позволяет осуществлять процесс перекрывания элементов данных конструктов - фрактальности и голографии, что обусловливает их взаимосодействие и постоянный переход идеального (фрактальность) в материальное образование (физика голограммы).