А так же их родителям...
Это я ко Всероссийскому учебному году решил написать.
Долго писать сейчас буду, надо еще пожрать приготовить, вот, параллельно и напишу.
Сразу скажу, что сам лично я вовсе не силен в математике. Мне разум избыточный мешает. Судите сами.
Я, например, прекрасно понимаю, что такое баран или пол- барана, но никогда не пойму, что такое баран, выраженный непериодической бесконечной десятичной дробью. Это какая- то бесконечная часть барана.
Ну, вот все же тут, кто будет это читать, гордятся своей образованность. Высшее образование, у некоторых даже два или три. Правда?
Вы считаете себя цивилизованными, современными, динамичными? Хм...
А все уверены в том, что математика, в частности, та самая, высшая или математический анализ, относится к современной цивилизации?
Пьер де Ферма, тот самый, XVII век, Карл Вейерштрасс XIX век, Мишель Ролль XVII- XVIII век, Жозеф Луи Лагранж XVII- XVIII век, Огюстен Луи Коши XVIII- XIX век, Рене Декарт XVI- XVII век, Леонардо Фибоначчи Пизанский XII- XIII век, Лука Пачоли, все бухгалтеры знают это имя? Или экономисты? Да, жил в XV- XVI веках.
Как ни странно, но ни одной русской фамилии. Не правда ли?
Ах, да, великий Николай Иванович Лобачевский. Википедия пишет, что родился 1 декабря 1792 года, умер 24 февраля 1856 года в Казани. Но вот казанские не дадут соврать, возле "Сковородки" на бывшей Ленина, ныне Кремлевской, стоит ему памятник, где написано, что дата рождения неизвестна. Посмотрите кто- нибудь.
Впрочем, я же обещал родителям, значит, речь о средней школе.
Пост задумывался несколько дней, а поводом к написанию стал телефонный разговор с мамой 10-ти летнего сына, которому она проверяет уроки. Вот и посмотрим.
Итак, две фразы:
1. Что я знаю о круге?
2. Кто и шутя, и скоро пожелает пи узнать, теперь уж знает.
О чем эти выражения, наполненные высокой поэтической выразительностью? С правописанием второго я могу ошибаться, потому что не знаю правил дореформенного русского языка, со всеми его - ять, - еръ, - еры и т п.
Да, ну, раз уж фраза сама о себе проболталась, то значит число
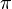
. О чем это число? Кто- нибудь может толком объяснить? Вот, лично я могу.
Предвосхищая фразу некоторых гуманитариев скажу:
Этому учили всех без исключения.
Можно, разумеется, залезть в Википедию, прочитать, но все равно не сможете объяснить, потому что понять не сможете.
Или вот, вспоминаю негодование моей матери:
- Я закончила школу 20 лет назад, откуда я могу помнить, что там преподавали. А у вас программа другая.
Знакомо? Наверняка большинство матерей именно так и говорят, когда речь об учебе ребенка старше 7-го класса средней школы. А вот почему я закончил школу 24 года назад, но помню это?
Или вот еще, не совсем имеющее отношение к математике, но тем не менее, число Авогадро, число Фибоначчи, то самое число Пи, синус и косинус, ускорение свободного падения... Кстати, величину этого ускорения, приближенно, должны знать абсолютно все. Именно благодаря ему вы, особенно дамы, становитесь на весы и после этого вес у вас выражается в килограммах.
Ой, даже не стану писать о Пифагоре 570-490 гг. до н. э, Евклиде ок. 300 г. до н. э, может еще кого припомнить из древних? Скажем Галилея, который жил в XVI- XVII веках.
Не, вряд ли современные, высоко образованные гуманитарии придают столько значения таким скучным вещам. А как быть с вещами не скучными?
Например, как своему сыну объяснить необходимость существования синуса или косинуса? Кто сможет?
Да, обещал же о числе Пи.
Тут, на самом деле, все просто. Речь о несоразмерности представления о пространстве. Мы живем в трехмерном мире, да- да, когда вы говорите о 3D, то речь именно об этом, длина- ширина- высота. Другого не дано. Если мне хоть кто- то сумеет здесь, в комментариях, четко и наглядно показать еще хотя бы одно измерение, то прямо здесь, на ваших глазах я поверю Лобачевскому и Эйнштейну.
Как нас учили находить длину окружности на практике? Да, взять веревочку или ниточку, обернуть вокруг стакана, а потом длину ниточки измерить. Но в отношении геометрии или пространств, которые выходит за размеры стакана, такой способ не подходит. Ну, не сможете вы обмотать веревкой земной шар.
Вот для этого и существует такой коэффициент пропорциональности, который связывает линейность и окружность. Плоскости и плоскости, образованные вращением. Любой многоугольник- это замкнутая ломанная линия, состоящая из отрезков, а окружность замкнута, но не изломанна. Вот и Пи для того, чтобы связать несвязываемое.
Кстати, окружности, шары, сферы, цилиндры существуют реально, в том числе и рукотворные, они стоят. Останкинская башня, купола соборов, мечетей, автомобильные колеса. Но фактически эти вещи существуют только в бесконечности. Если можно построить очень точный радиус, то есть, отрезок, необходимой длины, то обернув этот отрезок относительно начала или конца, мы получим окружность. Точную? Нет, потому что число Пи- бесконечная, непериодическая, десятичная дробь.
Или вот число Эйлера. Не говорите, что в школе не проходили. Натуральные логарифмы, смело в 10-м классе, как пить дать. Логарифм числа по основанию
e = 2.7182818284590452... называется натуральным логарифмом.
Да, а вот Гравитационная постоянная. Многие помнят, что такое Крутильные весы? Не, ну там дробь таки периодическая, если это, вообще, кому- либо, о чем либо говорит.
Пишу я пост и прямо вот балдею от самого себя, чувствую себя эдаким Пьером Ферма, который развлекался именно тем, что своим выдающимся образованным современникам задавал глупые вопросы и ржал над ними. Придворный шут, что с него взять?
Да, чтобы уже совсем не загромождать пост, расскажу о тригонометрических функциях. Просто для того, чтобы, когда сынулька спросит у мамульки, зачем ему вообще синусы- косинусы, мамулька бы не облажалась.
Переводить не стану слово тригонометрия, всем и так понятно, поскольку все прутся от гороскопов и знают слово Тригон. А смысл...
Ну, вот в чем измеряются стороны треугольника? Правильно в метрах.
А чем еще, кроме длин, характеризуется треугольник? Почему мы говорим о том, что в равностороннем треугольнике все углы равны 60 градусам?
Правильно! Бинго! Треугольник становится треугольником, замкнутой плоской фигурой, только после того как у него определены углы. А в чем измеряются углы? В градах, градусах, радианах. Правильно?
Так вот, для того, чтобы связать метры с градусами и существуют тригонометрические функции, не более. Ой, чота ржу!
Да, пора завязывать с этими загадками, все равно, половина не поймет. Хотя, в школе учились все. Абсолютно. И ТОП- блогеры и недотоп- не блогеры.
Да, еще была загадка о квадрате со сторонами ровно 1 метр. Его диагональ не существует фактически. Надо объяснять почему?
Или вот, число, очередное загадочное число, Золотое сечение. Ага, вот они Лука Пачоли и... да- да, тот самый Леонардо да Винчи, но, гуманитарии, это уже искусство, раз речь о Леонардо.
Вы же все, включая журналистов, искусствоведов, психологов, социологов, карьеристов и просто офисный планктон, просто обязаны знать о Золотом сечении?
Всё, я не могу больше. Уже давно под столом. От чего, не понятно.
Интересно, сколько заботливых родителей кинутся читать Википедию после прочтения моего поста?
Да, наличие в обиходе Числа Эйлера, Числа Пи, Постоянной Авогадро, Золотого сечения, ускорения свободного падения, Гравитационной постоянной, о чем говорят?
Да все просто. Мир хаотичен. Мир беспорядочен. Любая попытка упорядочить его приведет к смерти. И все упорядлочивание заключается в описании процессов, а управлять ими, извольте...
Впрочем, есть еще Циклы Карно, Броуновское движение, Корпускулярная теория Ломоносова, флуктуация и ароматы кварков.
Всё! Ушел жрать... или ржать.