Вероятностные алгоритмы.
Введение.
Традиционным образом (то есть, в самые последние сутки дедлайна) я поучаствовал в конкурсе, организованном ребятами из конторы Hola.
Задание было придумано очень крутое. "Очень крутое" -- это, в моём понимании, такое задание, которое:
Полностью условие можно почитать на офсайте, а вкратце оно звучит так:
Чтобы было повеселее, в тестах используется специальный генератор слов, которые визуально (и грамматически) очень похожи на нормальные английские, но при этом в словаре их нет, например: "goldrunk". И, напротив, в заданном словаре есть весьма странные записи, в которых распознать английский язык очень сложно, например, "qwertys" или "rRNA".
Согласно комментариям участников в соответствующем треде на хабрахабре, основные идеи (успешных) решений были следующие:
Я решил пойти немного другим путём, и сделал решение, основанное на использовании вероятностного алгоритма отличного от блумфильтра. Возможно, в конкретно данной ситуации оно и не показало самого оптимального результата, но, вообще, в целом, вероятностные алгоритмы -- это невероятно удобный инструмент, если хорошо его освоить. Я как раз давно хотел накатать про них какой-нибудь обзорный пост, но не было подходящего контекста. Поэтому, пользуясь случаем, делаю щас.
Немного теории.
В статье на русскоязычной википедии говорится, что: "Вероятностный алгоритм - алгоритм, предусматривающий обращение на определённых этапах своей работы к генератору случайных чисел с целью получения экономии во времени работы за счёт замены абсолютной достоверности результата достоверностью с некоторой вероятностью". Это не совсем так -- принципиально, к ГСЧ в вероятностных алгоритмах обращаться необязательно. В англоязычной версии этой статьи есть более корректное определение: "uniformly random bits". Опять же, экономия может достигаться не только во времени работы, а по памяти, например.
Неплохой демонстрацией может служить широко известный фильтр Блума, который является "вероятностной структурой данных". Источником "случайных" значений с дискретно-равномерным распределением здесь служит хеш-функция, а выигрыш получается в более экономном использовании памяти. Взамен мы получаем, правда, неуверенность в ответе: вместо да и нет мы имеем вероятно, да и точно нет. Эта неуверенность обусловлена вероятностью возникновения коллизии, но эту вероятность можно достаточно точно подобрать, чтобы применение блумфильтра было обосновано для конкретной задачи.
Соответственно, возможность такого рода компромисса в постановке задачи (значительный выигрыш по ресурсам взамен некоторой допустимой недостоверности ответа) может быть хорошим признаком того, что в решении имеет смысл использовать вероятностный алгоритм. Например, это конкурс про упаковку огромного словаря в 64Kb :)
Самое главное, что здесь нужно запомнить, это фразу: дискретно-равномерное распределение. "Равномерное распределение" на практике должно означать следующее: если случайная величина (ГСЧ, хэш-функция, значение сигнала) генерирует нам какое-то значение из интервала R, нужно, чтобы вероятность получения каждого значения из R была 1/R (или, хотя бы, очень близко к этому). При этом количество таких значений должно быть конечно (дискретно). Визуально, это выглядит следующим образом: допустим, мы взяли поле 10x10 и ткнули в рандомную точку. Получилось, например, как-то так:
А если мы воткнули их несколько тыщ, то должно получиться относительно равномерное покрытие, что-то типа такого:
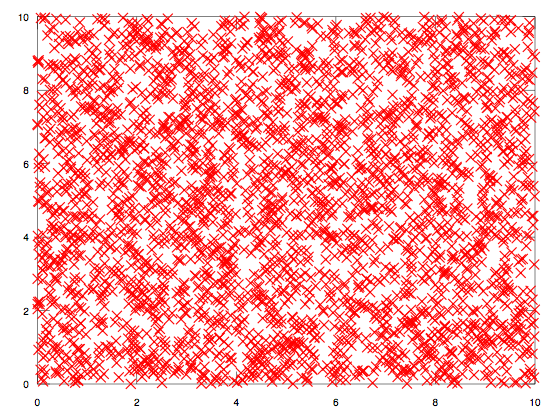
Соблюдение условия дискретно-равномерного распределения даёт нам возможность достаточно точно оценивать вероятности выпадения конкретных значений, которые могут нас интересовать в рамках моделирования наших алгоритмов. Без этой возможности мы теряем предсказуемость, что вырождает алгоритм в рандомный.
Так что перед реализацией вероятностного алгоритма надо обязательно проверять, что источник случайности в нашей задаче ведёт себя согласно дискретно-равномерному распределению. В большинстве случаев, достаточно просто взглянуть на график: например, в отличие от предыдущей картинки, вот эти значения явно не выглядят равномерно распределёнными:
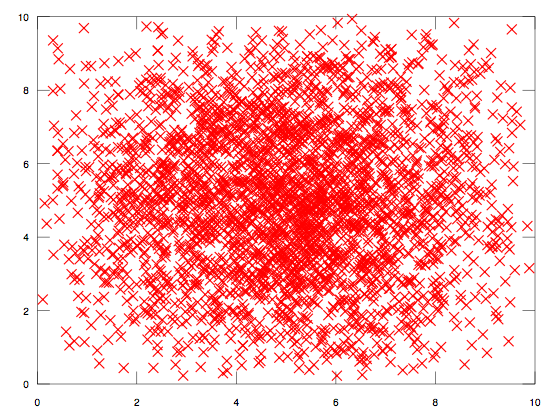
Нетрудно заметить, что координаты точек тяготеют к центру в (5,5), а по краям графика их, наоборот, очень мало. Не зная закона распределения в этом случае, мы не можем делать никаких предположений относительно вероятности выпадения конкретных интересующих нас координат, а, следовательно, не можем использовать этот источник случайности в вероятностном алгоритме.
Немного практики.
Из популярных практических алгоритмов для подобного рода задач я бы хотел отметить, например, такие:
Конкурсная задача.
Вернёмся к задаче про словарь. Итак, уже в условии однозначно написано про компромисс "допустимая недостоверность в обмен на ограниченные ресурсы". Следовательно, задачу можно пробовать решать вероятностным алгоритмом.
Самый простой вероятностный алгоритм, который можно придумать, это подбрасывание монетки:
function test(word) { return Math.random() < 0.5; }
Несложно догадаться, что он совершенно бесплатно даёт нам 50% правильных ответов, при этом даже не пользуясь своим аргументом :) Соответственно, это значение будет базисом, с которым можно сравнивать результативность других алгоритмов.
Далее, следующий из более-менее очевидных алгоритмов будет блумфильтр. В классической его реализации он для этой конкурсной задачи неприменим (ограничения по памяти слишком жёсткие, битовая маска нужного размера должна быть существенно больше заданного лимита), но многие участники пошли именно путём его адаптации. Например, специально подготавливая и фильтруя данные, или подбирая удачные хеш-функции.
Но, если понимать как работают вероятностные алгоритмы в принципе, можно попробовать придумать что-нибудь чуть более оригинальное. Я позаимствовал некоторые идеи из MinHash, и получилось вот что.
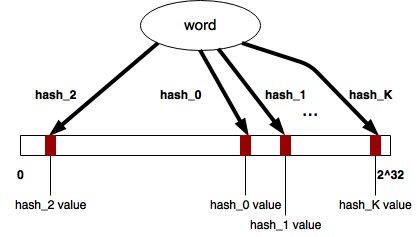
В качестве источника случайных значений я взял множество рандомных хеш-функций, как это сделано в minhash. Для этого я выбрал fnv (просто потому, что она мне нравится), которому я на вход подаю сначала случайное число, а потом сам аргумент.
Соответственно, набор таких случайных чисел (seeds) будет однозначно определять множество хеш-функций, которое будет использовано в задаче.
Применив K таких случайных хеш-функций к одному и тому же аргументу (например, слову из словаря) мы получим K результатов, которые будут, опять же, случайно распределены по всему диапазону значений fnv. Я взял 32-х битную версию, соответственно, результаты хеширования будут в диапазоне 0 - 0xffffffff. Дальше надо как-то убедиться, что эти результаты имеют равномерное распределение. Этот факт явно каким-то образом должен доказываться, но я, к сожалению, не математик, поэтому тупо нарисовал график и посмотрел на него глазами. Выглядит как равномерное :) Это свойство в данном случае мне важно для того, чтобы можно было оценить вероятность того, что случайная хэш-функция даст конкретное значение. При равномерном распределении эта вероятность будет 1/R, где R = 232.
Дальше сделаем вот что: возьмём одну такую случайную хеш-функцию H, и прогоним через неё все N слов из словаря. Получим N чисел (хешей слов), которые как-то случайным образом будут раскиданы в интервале от 0 до 232 - 1. Теперь нам надо найти какое-то такое утверждение P, которое бы:
Идея понятна: алгоритм получает слово, считает от него хеш с помощью хеш функции H, проверяет результат на условие P, и, если оно ложно, то это слово точно не из словаря. Если условие истинно, то слово, с какой-то вероятностью, может быть в словаре. С какой? Это зависит от природы утверждения P. Далее нам достаточно провести несколько проб (повторить алгоритм несколько раз для различных хеш-функций), с каждым разом увеличивая вероятность срабатывания P, чтобы достичь удовлетворяющей нас достоверности ответов.
Допустим, к примеру, сложилось такая ситуация, что все хеши слов из словаря оказались чётными. Тогда все нечётные значения из интервала от 0 до 232 означали бы true negative. Вероятность этой ситуации (хеш проверяемого слова оказался нечётным) была бы почти 0.5 -- это очень крутой результат для одной только пробы. Ведь тогда нам для достоверности ответа "слова точно нет в словаре" в 99% достаточно log0.50.01 = ~7 проб, то есть, всего семь рандомных хеш-функций.
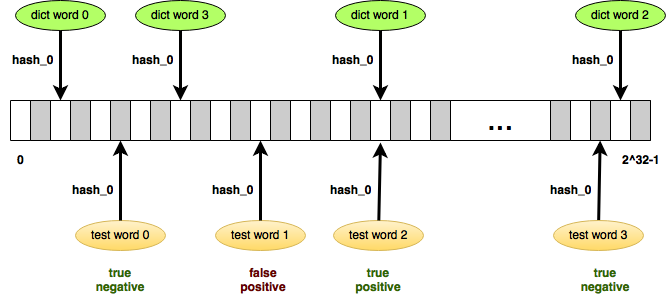
Но, конечно, в нашем случае настолько удачная конфигурация практически невозможна при таком количестве случайных значений. Это всё равно, что 660 тысяч раз подбросить монетку (по количеству слов из словаря), и чтобы при этом выпали все орлы.
Конкретно под наш словарь можно попробовать делить всё множество значений хеш-функций не на две корзины (чётные и нечётные числа), а на большее количество: M > 2. Тогда нашей задачей будет подобрать для каждой используемой хеш-функции такое (в идеале, минимальное) количество корзин, чтобы при хешировании всех слов из словаря одна из корзин оказалась пустой.
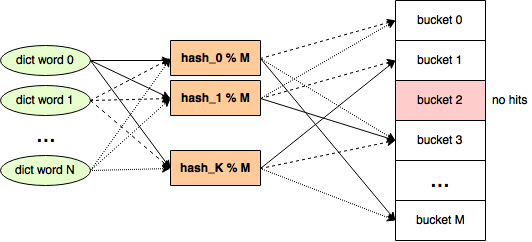
Если значения хеш-функций имеют равномерное распределение (а они имеют в нашем случае), вероятность попадания хеша в одну из корзин будет равняться 1/M. Каким же должен быть M, чтобы, раскидав по этому такому количеству корзин 660 тысяч хешей, у нас бы осталась одна пустая корзина? Это как-то явно подсчитывается при помощи математики, но (если вы, подобно мне, ничерта не помите из тервера) можно немного схалтурить, и получить нужные цифры при помощи несложного программирования.
Проведём эксперимент: сгенерируем нужное количество 32-х битных случайных чисел, по одному на слово из словаря -- как будто, это результаты хеширования. Программный ГСЧ должен давать равномерное распределение, и хеш-функция тоже даёт равномерное распределение, так что это относительно равноценная замена. Далее тупо брутфорсом попробуем подобрать минимальное количество корзин так, чтобы в одну из них ни одно рандомное число не попало. Вот как это примерно может выглядеть на Common Lisp:
(defun get-minimum-buckets-count (words-count) (iter ;; generate pseudo hashes (with pseudo-hashes = (iter (repeat words-count) (collect (random (ash 1 32)) result-type simple-vector))) (for buckets-count from 2) ;; make buckets with hit counters (for buckets-hits = (make-array buckets-count :element-type 'fixnum :initial-element 0)) ;; collect hits (iter (for i from 0) (for hash in-sequence pseudo-hashes) (for bucket = (mod hash buckets-count)) (incf (elt buckets-hits bucket))) ;; check whether an empty bucket exists (for empty-bucket = (position 0 buckets-hits)) (when empty-bucket (return-from get-minimum-buckets-count (values buckets-count empty-bucket)))))
Небольшое отступление: даже если вы уверено считаете считаете такие вещи формулами, я, в принципе, рекомендую не лениться, и всё равно проверять свои гипотезы с помощью подобного рода кода. Пишутся такие микро-программки три минуты, но позволяют достаточно точно смоделировать рассматриваемую задачу, и потенциально выявить некоторые моменты, которые легко упустить при рассуждениях в уме.
Запустив эту функцию для 660000 слов, мы (через некоторое время) получим результат для M порядка ~33000. Разумеется, при каждом запуске он будет разный (так как псевдо-хеши генерируются каждый раз случайным образом), но это будут всегда приблизительно одинаковые значения с небольшим разбросом. На практике это означает, что мы можем получить с одной пробы вероятность 0.00003, что слово не входит в заданный словарь: для этого достаточно проверить, что хеш слова попал в пустую корзину. На первый взгляд совсем мизерный шанс, но давайте прикинем, что с этого можно получить.
Итак, мы можем взять одну рандомную хеш функцию H0, словарь, и найти для них два числа: M0 (минимальное количество корзин, раскидывая хеши по которым образуется одна пустая), и B0 (номер пустой корзины). Эти два числа описывают пробу P0, которая даёт шанс в 0.003%, что проверяемое слово точно не принадлежит словарю. Если же мы посчитаем таким же образом P1 для другой функции H1, мы сможем провести две независимые пробы, увеличив вероятность true negative до 0.00006 (вероятность не попасть в пустую корзину для одной пробы равняется 1.0 - 0.00003 = 0.99997, а для двух независимых проб вероятности умножаются). Аналогично, десять подобных проб дадут уже вероятность в 0.03%, сто в 0.3%, а десять тысяч, например, целых 26.1%. Продолжая этот ряд, можно подобрать число 153000 -- именно столько проб нужно выполнить, чтобы с вероятностью 99% определить true negative.
Одна проба однозначно задаётся двумя числами M и B, соответственно, для 150-ти тысяч проб нужно сохранить 300 тысяч чисел. Это явно больше того, что можно запихать в заданные задачей лимиты. Нетрудно прикинуть, что, если мы аллоцируем, ориентировочно 14 бит для M и 15 бит для B, в 64 Kb можно вместить всего порядка 18000 проб. А ведь там ещё должно остаться какое-то место для сценария на js! Соответственно, чуть более реалистичная цифра в 17000 проб даст вероятность определения true negative в ~40%.
Что это означает на практике? Это означает следующие вещи:
Итоговый процент верных ответов зависит от характера тестовых данных: в худшем случае он будет стремиться к 40% (если на вход подаются только слова не из словаря), в лучшем -- к 100% (если на входе только слова из словаря), а в случае половина тех, и половина других, это должно быть значение порядка 70%.
Эту цифру можно чуть-чуть улучшить, параллельно значительно упростив формат сериализованной пробы (что тоже немаловажно, ведь размер js-скрипта тоже имеет значение). Можно подбирать M специальным образом, чтобы пустая корзина оказывалась всегда, например, в нулевой позиции (B == 0, или H % M == 0). В этом случае для записи пробы нам достаточно только одного числа M. Эксперименты показывают, что это получаются значения из диапазона примерно 38000 - 91000: это означает, что соответствующие вероятности для проб будут меньше, но зато для их упаковки теперь достаточно 16 бит, следовательно количество проб можно увеличить до ~32000, и, главное, сильно упростить код для их упаковки/распаковки.
Конечно, полученная цифра в 70% верных ответов выглядит не очень впечатляюще. Но следует отметить две вещи про это решение:
В целом, надеюсь, мне удалось более-менее доступно рассказать про вероятностные алгоритмы, и подать идею, как их можно применять на примере решения этой конкурсной задачи. Из минусов конкретно моего подхода следует отметить серьёзную ресурсоёмкость этапа компиляции, когда происходит подбор брутфорсом значений M для проб. Собственно, из-за этой ресурсоёмкости мне так и не удалось уложиться в дедлайн конкурса, потому что банально не нашёл вовремя достаточно мощной машины с десятком-другим свободных ядер :)
Полностью моё решение, вместе с расчитанными данными, можно взять в этом репо: сами хеши я породил из js (директория generator), а компилятор проб из них сделал на Rust (директория compiler).
Традиционным образом (то есть, в самые последние сутки дедлайна) я поучаствовал в конкурсе, организованном ребятами из конторы Hola.
Задание было придумано очень крутое. "Очень крутое" -- это, в моём понимании, такое задание, которое:
- Имеет практическую ценность.
- Не подразумевает одного единственного верного решения, до которого просто нужно додуматься в процессе конкурса.
Полностью условие можно почитать на офсайте, а вкратце оно звучит так:
- Дан словарь из ~660k записей. Ориентировочно, это английские слова.
- Надо написать функцию "test(word)", которая возвращает true, если заданное слово входит в словарь, и false, если нет.
- Суммарный объём программы и файла с данными, которым она может пользоваться, не должен превышать 65536 байт.
- Побеждает решение, которое даст максимальный процент правильных ответов на большом количестве тестов.
Чтобы было повеселее, в тестах используется специальный генератор слов, которые визуально (и грамматически) очень похожи на нормальные английские, но при этом в словаре их нет, например: "goldrunk". И, напротив, в заданном словаре есть весьма странные записи, в которых распознать английский язык очень сложно, например, "qwertys" или "rRNA".
Согласно комментариям участников в соответствующем треде на хабрахабре, основные идеи (успешных) решений были следующие:
- Максимальное обрезание словаря, выделение значащих префиксов/суффиксов/нграмм, и последующее запихивание всего этого в фильтр Блума.
- Машинное обучение. В основном, это разновидности деревьев решений.
- Решения, воссоздающие словарь из тестовых данных в рантайме.
Я решил пойти немного другим путём, и сделал решение, основанное на использовании вероятностного алгоритма отличного от блумфильтра. Возможно, в конкретно данной ситуации оно и не показало самого оптимального результата, но, вообще, в целом, вероятностные алгоритмы -- это невероятно удобный инструмент, если хорошо его освоить. Я как раз давно хотел накатать про них какой-нибудь обзорный пост, но не было подходящего контекста. Поэтому, пользуясь случаем, делаю щас.
Немного теории.
В статье на русскоязычной википедии говорится, что: "Вероятностный алгоритм - алгоритм, предусматривающий обращение на определённых этапах своей работы к генератору случайных чисел с целью получения экономии во времени работы за счёт замены абсолютной достоверности результата достоверностью с некоторой вероятностью". Это не совсем так -- принципиально, к ГСЧ в вероятностных алгоритмах обращаться необязательно. В англоязычной версии этой статьи есть более корректное определение: "uniformly random bits". Опять же, экономия может достигаться не только во времени работы, а по памяти, например.
Неплохой демонстрацией может служить широко известный фильтр Блума, который является "вероятностной структурой данных". Источником "случайных" значений с дискретно-равномерным распределением здесь служит хеш-функция, а выигрыш получается в более экономном использовании памяти. Взамен мы получаем, правда, неуверенность в ответе: вместо да и нет мы имеем вероятно, да и точно нет. Эта неуверенность обусловлена вероятностью возникновения коллизии, но эту вероятность можно достаточно точно подобрать, чтобы применение блумфильтра было обосновано для конкретной задачи.
Соответственно, возможность такого рода компромисса в постановке задачи (значительный выигрыш по ресурсам взамен некоторой допустимой недостоверности ответа) может быть хорошим признаком того, что в решении имеет смысл использовать вероятностный алгоритм. Например, это конкурс про упаковку огромного словаря в 64Kb :)
Самое главное, что здесь нужно запомнить, это фразу: дискретно-равномерное распределение. "Равномерное распределение" на практике должно означать следующее: если случайная величина (ГСЧ, хэш-функция, значение сигнала) генерирует нам какое-то значение из интервала R, нужно, чтобы вероятность получения каждого значения из R была 1/R (или, хотя бы, очень близко к этому). При этом количество таких значений должно быть конечно (дискретно). Визуально, это выглядит следующим образом: допустим, мы взяли поле 10x10 и ткнули в рандомную точку. Получилось, например, как-то так:

А если мы воткнули их несколько тыщ, то должно получиться относительно равномерное покрытие, что-то типа такого:

Соблюдение условия дискретно-равномерного распределения даёт нам возможность достаточно точно оценивать вероятности выпадения конкретных значений, которые могут нас интересовать в рамках моделирования наших алгоритмов. Без этой возможности мы теряем предсказуемость, что вырождает алгоритм в рандомный.
Так что перед реализацией вероятностного алгоритма надо обязательно проверять, что источник случайности в нашей задаче ведёт себя согласно дискретно-равномерному распределению. В большинстве случаев, достаточно просто взглянуть на график: например, в отличие от предыдущей картинки, вот эти значения явно не выглядят равномерно распределёнными:

Нетрудно заметить, что координаты точек тяготеют к центру в (5,5), а по краям графика их, наоборот, очень мало. Не зная закона распределения в этом случае, мы не можем делать никаких предположений относительно вероятности выпадения конкретных интересующих нас координат, а, следовательно, не можем использовать этот источник случайности в вероятностном алгоритме.
Немного практики.
Из популярных практических алгоритмов для подобного рода задач я бы хотел отметить, например, такие:
- Locality-sensitive hashing: подбирает для множества элементов хэш-функцию таким образом, что "схожие" элементы попадают в одну корзину (хеши дают коллизию ожидаемым образом). Таким образом достигается существенное уменьшение размерности данных, и используется, например, в задачах кластеризации.
- MinHash: ускорение расчёта коэффициента Жаккара для вычисления степени схожести двух множеств. Широко используется, например, для задач выявления нечётких дубликатов среди большого количества документов.
- Семплирование потока данных. В отличие от простой выборки каждого N-ого элемента из потока, хешируют некоторый составной ключ (например, "пользователь"/"запрос"/"таймстамп"), после чего берут N корзин, и отбрасывают все результаты, не попавшие в одну из них. Это позволяет семплировать поток по сложным условиям, избегая дорогостоящей группировки.
- Flajolet-Martin algorithm, и его развитие в виде HyperLogLog. Алгоритмы используют достаточно изящный хак для быстрой аппроксимации количества уникальных элементов в заданном множестве. Я реально советую ознакомится с описанием, это, действительно, хитрый трюк :)
Конкурсная задача.
Вернёмся к задаче про словарь. Итак, уже в условии однозначно написано про компромисс "допустимая недостоверность в обмен на ограниченные ресурсы". Следовательно, задачу можно пробовать решать вероятностным алгоритмом.
Самый простой вероятностный алгоритм, который можно придумать, это подбрасывание монетки:
function test(word) { return Math.random() < 0.5; }
Несложно догадаться, что он совершенно бесплатно даёт нам 50% правильных ответов, при этом даже не пользуясь своим аргументом :) Соответственно, это значение будет базисом, с которым можно сравнивать результативность других алгоритмов.
Далее, следующий из более-менее очевидных алгоритмов будет блумфильтр. В классической его реализации он для этой конкурсной задачи неприменим (ограничения по памяти слишком жёсткие, битовая маска нужного размера должна быть существенно больше заданного лимита), но многие участники пошли именно путём его адаптации. Например, специально подготавливая и фильтруя данные, или подбирая удачные хеш-функции.
Но, если понимать как работают вероятностные алгоритмы в принципе, можно попробовать придумать что-нибудь чуть более оригинальное. Я позаимствовал некоторые идеи из MinHash, и получилось вот что.
В качестве источника случайных значений я взял множество рандомных хеш-функций, как это сделано в minhash. Для этого я выбрал fnv (просто потому, что она мне нравится), которому я на вход подаю сначала случайное число, а потом сам аргумент.
Соответственно, набор таких случайных чисел (seeds) будет однозначно определять множество хеш-функций, которое будет использовано в задаче.
Применив K таких случайных хеш-функций к одному и тому же аргументу (например, слову из словаря) мы получим K результатов, которые будут, опять же, случайно распределены по всему диапазону значений fnv. Я взял 32-х битную версию, соответственно, результаты хеширования будут в диапазоне 0 - 0xffffffff. Дальше надо как-то убедиться, что эти результаты имеют равномерное распределение. Этот факт явно каким-то образом должен доказываться, но я, к сожалению, не математик, поэтому тупо нарисовал график и посмотрел на него глазами. Выглядит как равномерное :) Это свойство в данном случае мне важно для того, чтобы можно было оценить вероятность того, что случайная хэш-функция даст конкретное значение. При равномерном распределении эта вероятность будет 1/R, где R = 232.

Дальше сделаем вот что: возьмём одну такую случайную хеш-функцию H, и прогоним через неё все N слов из словаря. Получим N чисел (хешей слов), которые как-то случайным образом будут раскиданы в интервале от 0 до 232 - 1. Теперь нам надо найти какое-то такое утверждение P, которое бы:
- Выполнялось бы для всех полученных чисел.
- Не выполнялось для как можно большего количества остальных чисел из [0, 232).
Идея понятна: алгоритм получает слово, считает от него хеш с помощью хеш функции H, проверяет результат на условие P, и, если оно ложно, то это слово точно не из словаря. Если условие истинно, то слово, с какой-то вероятностью, может быть в словаре. С какой? Это зависит от природы утверждения P. Далее нам достаточно провести несколько проб (повторить алгоритм несколько раз для различных хеш-функций), с каждым разом увеличивая вероятность срабатывания P, чтобы достичь удовлетворяющей нас достоверности ответов.
Допустим, к примеру, сложилось такая ситуация, что все хеши слов из словаря оказались чётными. Тогда все нечётные значения из интервала от 0 до 232 означали бы true negative. Вероятность этой ситуации (хеш проверяемого слова оказался нечётным) была бы почти 0.5 -- это очень крутой результат для одной только пробы. Ведь тогда нам для достоверности ответа "слова точно нет в словаре" в 99% достаточно log0.50.01 = ~7 проб, то есть, всего семь рандомных хеш-функций.

Но, конечно, в нашем случае настолько удачная конфигурация практически невозможна при таком количестве случайных значений. Это всё равно, что 660 тысяч раз подбросить монетку (по количеству слов из словаря), и чтобы при этом выпали все орлы.
Конкретно под наш словарь можно попробовать делить всё множество значений хеш-функций не на две корзины (чётные и нечётные числа), а на большее количество: M > 2. Тогда нашей задачей будет подобрать для каждой используемой хеш-функции такое (в идеале, минимальное) количество корзин, чтобы при хешировании всех слов из словаря одна из корзин оказалась пустой.

Если значения хеш-функций имеют равномерное распределение (а они имеют в нашем случае), вероятность попадания хеша в одну из корзин будет равняться 1/M. Каким же должен быть M, чтобы, раскидав по этому такому количеству корзин 660 тысяч хешей, у нас бы осталась одна пустая корзина? Это как-то явно подсчитывается при помощи математики, но (если вы, подобно мне, ничерта не помите из тервера) можно немного схалтурить, и получить нужные цифры при помощи несложного программирования.
Проведём эксперимент: сгенерируем нужное количество 32-х битных случайных чисел, по одному на слово из словаря -- как будто, это результаты хеширования. Программный ГСЧ должен давать равномерное распределение, и хеш-функция тоже даёт равномерное распределение, так что это относительно равноценная замена. Далее тупо брутфорсом попробуем подобрать минимальное количество корзин так, чтобы в одну из них ни одно рандомное число не попало. Вот как это примерно может выглядеть на Common Lisp:
(defun get-minimum-buckets-count (words-count) (iter ;; generate pseudo hashes (with pseudo-hashes = (iter (repeat words-count) (collect (random (ash 1 32)) result-type simple-vector))) (for buckets-count from 2) ;; make buckets with hit counters (for buckets-hits = (make-array buckets-count :element-type 'fixnum :initial-element 0)) ;; collect hits (iter (for i from 0) (for hash in-sequence pseudo-hashes) (for bucket = (mod hash buckets-count)) (incf (elt buckets-hits bucket))) ;; check whether an empty bucket exists (for empty-bucket = (position 0 buckets-hits)) (when empty-bucket (return-from get-minimum-buckets-count (values buckets-count empty-bucket)))))
Небольшое отступление: даже если вы уверено считаете считаете такие вещи формулами, я, в принципе, рекомендую не лениться, и всё равно проверять свои гипотезы с помощью подобного рода кода. Пишутся такие микро-программки три минуты, но позволяют достаточно точно смоделировать рассматриваемую задачу, и потенциально выявить некоторые моменты, которые легко упустить при рассуждениях в уме.
Запустив эту функцию для 660000 слов, мы (через некоторое время) получим результат для M порядка ~33000. Разумеется, при каждом запуске он будет разный (так как псевдо-хеши генерируются каждый раз случайным образом), но это будут всегда приблизительно одинаковые значения с небольшим разбросом. На практике это означает, что мы можем получить с одной пробы вероятность 0.00003, что слово не входит в заданный словарь: для этого достаточно проверить, что хеш слова попал в пустую корзину. На первый взгляд совсем мизерный шанс, но давайте прикинем, что с этого можно получить.
Итак, мы можем взять одну рандомную хеш функцию H0, словарь, и найти для них два числа: M0 (минимальное количество корзин, раскидывая хеши по которым образуется одна пустая), и B0 (номер пустой корзины). Эти два числа описывают пробу P0, которая даёт шанс в 0.003%, что проверяемое слово точно не принадлежит словарю. Если же мы посчитаем таким же образом P1 для другой функции H1, мы сможем провести две независимые пробы, увеличив вероятность true negative до 0.00006 (вероятность не попасть в пустую корзину для одной пробы равняется 1.0 - 0.00003 = 0.99997, а для двух независимых проб вероятности умножаются). Аналогично, десять подобных проб дадут уже вероятность в 0.03%, сто в 0.3%, а десять тысяч, например, целых 26.1%. Продолжая этот ряд, можно подобрать число 153000 -- именно столько проб нужно выполнить, чтобы с вероятностью 99% определить true negative.
Одна проба однозначно задаётся двумя числами M и B, соответственно, для 150-ти тысяч проб нужно сохранить 300 тысяч чисел. Это явно больше того, что можно запихать в заданные задачей лимиты. Нетрудно прикинуть, что, если мы аллоцируем, ориентировочно 14 бит для M и 15 бит для B, в 64 Kb можно вместить всего порядка 18000 проб. А ведь там ещё должно остаться какое-то место для сценария на js! Соответственно, чуть более реалистичная цифра в 17000 проб даст вероятность определения true negative в ~40%.
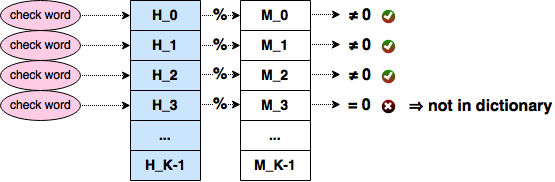
Что это означает на практике? Это означает следующие вещи:
- Если на вход функции test было подано слово из словаря, все пробы будут успешными (хеши не попадут в пустые корзины), и будет возвращена истина. Это true positive.
- Если на вход функции test было подано слово не из словаря, то:
- с вероятностью 40% одна из проб даст неуспех (один из хешей попадёт в пустую корзину), и будет возвращена ложь. Это true negative.
- с вероятностью 60% все пробы, всё же, дадут успех, и будет возвращена истина. Это false positive.
- Ситуация false negative в данной конфигурации невозможна, потому что мы, формируя множество проб, специально так подбирали числа M, чтобы для слов из словаря обязательно оставалась пустая корзина.
Итоговый процент верных ответов зависит от характера тестовых данных: в худшем случае он будет стремиться к 40% (если на вход подаются только слова не из словаря), в лучшем -- к 100% (если на входе только слова из словаря), а в случае половина тех, и половина других, это должно быть значение порядка 70%.
Эту цифру можно чуть-чуть улучшить, параллельно значительно упростив формат сериализованной пробы (что тоже немаловажно, ведь размер js-скрипта тоже имеет значение). Можно подбирать M специальным образом, чтобы пустая корзина оказывалась всегда, например, в нулевой позиции (B == 0, или H % M == 0). В этом случае для записи пробы нам достаточно только одного числа M. Эксперименты показывают, что это получаются значения из диапазона примерно 38000 - 91000: это означает, что соответствующие вероятности для проб будут меньше, но зато для их упаковки теперь достаточно 16 бит, следовательно количество проб можно увеличить до ~32000, и, главное, сильно упростить код для их упаковки/распаковки.

Конечно, полученная цифра в 70% верных ответов выглядит не очень впечатляюще. Но следует отметить две вещи про это решение:
- Удивительная простота алгоритма в целом, и элементарная масштабируемость: для достижения нужной точности нужно просто последовательно увеличивать количество проб.
- Это абсолютно "чистый" и "честный" результат: на нетронутых оригинальных входных данных, когда словарь взят полностью как есть. Всегда можно приложить некоторые усилия к препроцессингу: порезать слова, оканчивающиеся на "'s", разделить на префиксы/суффиксы, и т.п. Ребята в комментариях к задаче на хабрахабре писали, что они относительно безболезненно уменьшали словарь до 280000 записей. А 280 тысяч хешей в нашем алгоритме уже означают M ~ 13000, что, в свою очередь, даёт вероятность одной пробы 0.0076% и порядка 18000 проб в 64 Kb, выдающих, суммарно, почти 75% true negative! А это уже больше 87% верных ответов для случая 50/50 словарных и не словарных слов.
В целом, надеюсь, мне удалось более-менее доступно рассказать про вероятностные алгоритмы, и подать идею, как их можно применять на примере решения этой конкурсной задачи. Из минусов конкретно моего подхода следует отметить серьёзную ресурсоёмкость этапа компиляции, когда происходит подбор брутфорсом значений M для проб. Собственно, из-за этой ресурсоёмкости мне так и не удалось уложиться в дедлайн конкурса, потому что банально не нашёл вовремя достаточно мощной машины с десятком-другим свободных ядер :)
Полностью моё решение, вместе с расчитанными данными, можно взять в этом репо: сами хеши я породил из js (директория generator), а компилятор проб из них сделал на Rust (директория compiler).