Note to self: math is weird
I’m not going to lie to you: having taken Calculus 2 and passed (with the A? We’ll find out on Monday) I’m still uncertain if I understand the damn stuff. However, having used some of it today, I feel pretty proud.
I was browsing Wikipedia regarding some details of Zeno’s Paradox (you know, like cool people are wont to do) and I hit upon a link regarding the number .9 repeating (a decimal followed by an endless string of 9s). Wikipedia informed me that .9999... is equal to 1. At this point I balked from annoyance. Even moreso when Wikipedia proceeded to inform me that generally un-smart people have difficulty understanding this.
Ah! A challenge.
So I whipped out some scrap paper and decided to look at .9999... as a mathematical, indeed a geometric, sequence (.9 + .09 + .009 + .0009 ad infinitum.) You see, Calc 2 has the power to resolve such things! Essentially, you can look at the sequence and, supposing several aspects remain constant, determine to where the series converges; the sum of all numbers in the infinite sequence.
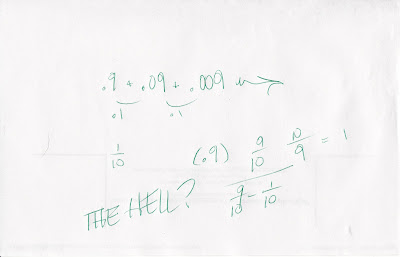
It equals 1! I think my written comment highlights my mood regarding the situation well enough.
I was browsing Wikipedia regarding some details of Zeno’s Paradox (you know, like cool people are wont to do) and I hit upon a link regarding the number .9 repeating (a decimal followed by an endless string of 9s). Wikipedia informed me that .9999... is equal to 1. At this point I balked from annoyance. Even moreso when Wikipedia proceeded to inform me that generally un-smart people have difficulty understanding this.
Ah! A challenge.
So I whipped out some scrap paper and decided to look at .9999... as a mathematical, indeed a geometric, sequence (.9 + .09 + .009 + .0009 ad infinitum.) You see, Calc 2 has the power to resolve such things! Essentially, you can look at the sequence and, supposing several aspects remain constant, determine to where the series converges; the sum of all numbers in the infinite sequence.
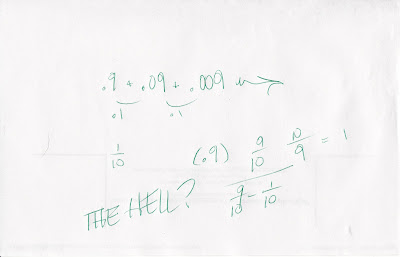
It equals 1! I think my written comment highlights my mood regarding the situation well enough.