The causal structure of black holes
A commenter writing about my earlier post, "Relativity, FTL and Causality" said:
As far as FTL being equivalent to time travel, the above explanation is correct. As far as FTL being impossible at present, it is not quite. Richard's explanation lacks a mention of black holes. An object (with non-zero mass), falling into a black hole from rest, will cross the event horizon AT THE SPEED OF LIGHT. Unfortunately we (the distant observers) would not be able to witness this event, since the falling observer would take forever (from our viewpoint) to reach the event horizon. In the falling observer's reference frame, however, he'd be flying at the speed of light all right! Moreover, he'd probably be able to time travel as well, as his speed continues to increase (to >c) inside the event horizon. Whether this would lead to any causality violations is unknown, since we can't see past the event horizon, and the unfortunate falling observer has a short time to live before he hits singularity, causality violations or not. However, from a purely theoretical point of view, we know that FTL travel is possible with black holes.
This comment about black holes is not true, at least in general relativity, the relativistic theory of gravity. It's correct that the radial velocity of an infalling object goes to zero at the event horizon when expressed in the coordinates of an inertial observer who is stationary with respect to the black hole and far away from it. In other words, the distant observer sees the falling object approach the horizon but never cross it. However, if a second observer falls in a windowless[1] spaceship she would notice nothing out of the ordinary, except for tidal effects, as she crosses the event horizon. If the tidal effects are sufficiently small (they can be made arbitrarily small by increasing the mass of the black hole) then she'd have no way of knowing whether she was falling into a black hole or just drifting through space. This is one aspect of a general feature of general relativistic spacetimes: as the region considered gets smaller and smaller it looks more and more like the spacetime of special relativity. Moreover, there's no frame in which her trajectory becomes spacelike so she can't be said to be travelling faster than light.
On the other hand, there's clearly something special about the event horizon of a black hole, and the singularity in its interior. What happens in a black hole spacetime is that the light cones near the black hole are "tilted" compared with what a naive observer at far away from the hole might expect. At the event horizon the tilting becomes so great that there are no future timelike or lightlike trajectories that can escape to infinity. The singularity is therefore not really at the "centre" of the black hole - although it looks that way in the coordinate system of the distant inertial observer - but rather in the future of all observers who fall across the horizon. And typically, and unfortunately for our daring black-hole explorer, not that far in the future.
One way to visualise this is through the use of Penrose diagrams. These are diagrams of the causal structure of a spacetime in which the points infinitely far away in space or time have been drawn at finite distances on the diagram through the use of a "conformal mapping" that leaves the causal structure intact. (The conformal mapping distorts the geometry of the spacetime to more clearly show its causal structure.) Rays of light in these diagrams still travel at 45 degrees to the vertical as in all of my Minkowski diagrams. The edges of the diagram are then the regions of timelike, spacelike and lightlike infinity - and singularities at a finite distance. This all sounds rather arcane, so let's look at an example:
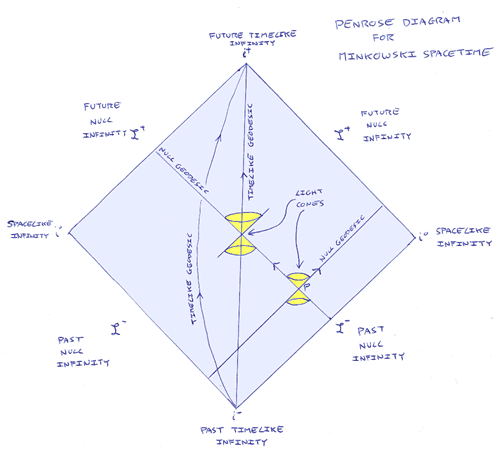
Figure 1 The causal structure of Minkowski spacetime
On this diagram I've shown two possible paths for freely falling observers. (These paths are technically called "timelike geodesics".). Just as in my other diagrams of spacetime, at each event along the timelike path the path itself is in the light cone of the event, so all observers with mass travel slower than light. If we follow either of the two example paths - or indeed any timelike geodesic - forward in time we reach the region called "future timelike infinity". If we follow them backwards in time we reach "past timelike infinity". Similarly, light rays can shine from "past null infinity" and can extend in the future to "future null infinity". As we might expect, all the edges of this diagram are the appropriate kinds of infinity as Minkowski spacetime extends infinitely in space and time from any given event.
Now let's take a look at the causal structure of a spacetime that contains a spherical, uncharged, non-rotating star collapsing to form a black hole. (The spacetime for an eternally existing black hole has features I don't wish to discuss here.) In this case the spacetime outside the star isn't a Minkowski spacetime but a Schwarzschild spacetime. However, causally - and remember that Penrose diagrams show only the causal structure and not the geometry - the outside region is very much like Minkowski spacetime. The inside is very different though.
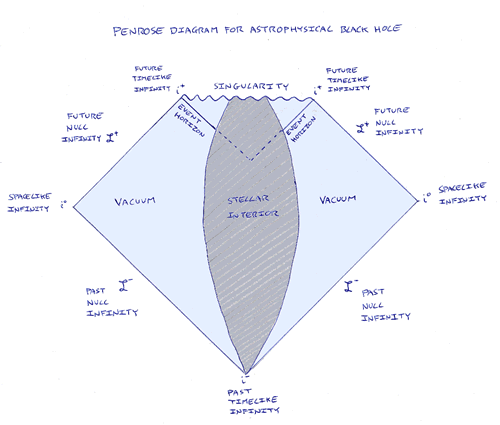
Figure 1 The causal structure of a physically realistic black hole spacetime. (The wiggles in the singularity are a notational convention and are not supposed to indicate any structure in the singularity itself.)
Once again, outgoing light rays originating from anywhere in the exterior vacuum region can reach future null infinity and (some) freely falling matter particles can reach future timelike infinity. But the diagram clearly shows that a light ray or matter particle from the region inside the event horizon of the black hole cannot reach future null or timelike infinity respectively. No matter in which direction or at what speed particles inside the horizon move, they can only ever reach the singularity. The singularity itself is a spacelike hypersurface on which all world-lines passing through the event horizon terminate. To escape from it, one would have to be able to travel faster than light. Otherwise it is, very literally, the end of time.
[1] If she were fortunate(?) enough to have windows to observe the outside world she'd see some strange things that I won't discuss here.