Ма́ндала (санскр. मण्डल - круг, диск; тиб. དཀྱིལ་འཁོར, Вайли dkyil 'khor; монг. мандал)
Ма́ндала (санскр. मण्डल - круг, диск; тиб. དཀྱིལ་འཁོར, Вайли dkyil 'khor; монг. мандал)
Ма́ндала (санскр. मण्डल - круг, диск; тиб. དཀྱིལ་འཁོར, Вайли dkyil 'khor; монг. мандал) - сакральное схематическое изображение либо конструкция, используемая в буддийских и индуистских религиозных практиках.
http://ru.wikipedia.org/wiki/%CC%E0%ED%E4%E0%EB%E0

Мандала - это символ колеса жизни и смерти, космических процессов существования, планет и звезд, земных сезонов и галактических циклов.

МАНДАЛА (др.-инд. «mándala», «круг», «диск», «круглый», «круговой» и т. п.), один из основных сакральных символов в буддийской мифологии; ритуальный предмет, воплощающий символ; вид ритуального подношения (включая и жертву).
Замечательной чертой храмового (а также светского) строительства в Индии является то, что все индуистские храмы возводились по одному и тому же «строительному плану», который назывался Vāstu-purusa-mandala. Это слово толкуется следующим образом: «мандала» означает «план, схема, ритуальная диаграмма»; Пуруша - это космический человек, воплощающий в себе универсальное Бытие, начало, наполнение и суть всего (см. гимн в его честь в «Ригведе», X, 90); «васту» означает «место, вместилище». Таким образом, « Васту-пуруша-мандала» - не что иное, как «диаграмма местопребывания Пуруши», или план Космоса, воплощаемый на земле в виде храма, или образ Пуруши, его подобие. Итак, форма любого индуистского храма, его смысл и значение определяются этим планом-космограммой, регулируются им (существовали и другие виды мандал. Но это - символический план, а не план реального храма и не план местности, где он строился.
Архитектор (стхапати), строивший храм, должен был обладать, кроме архитектурной техники, знаниями всей философско-религиозной традиции, воплощаемой в создании мандалы: ведь строительство храмов в очень большой степени было связано с наблюдениями за небесными светилами, астрологией и астрономией, со сложными ритуалами («Манусамхита», VII, 47-48). Каждое движение при натягивании шнура и черчении линий мандалы на месте будущего храма было ритуальным и космически значимым. Вот почему это искусство рано нашло свое отражение в ведической литературе. В частности, традиционной архитектуре были посвящены специальные пособия - Vāstu-śāstras.
Как же выглядит строительная мандала? Это прежде всего квадрат в плане, ориентированный по странам света, и таковы все индуистские храмы, это их фундаментальная форма Мандала может быть выгравирована на камне или на алтаре, ее чертили на земле перед строительством храма в натуральную величину или же символически. По мнению Крамриш, квадрат предполагает круг и его в конечном итоге продуцирует; круг и квадрат координируют друг с другом в архитектуре Индии, начиная с ведического огненного алтаря Агни.
http://www.sunhome.ru/journal/51229

Скажите пожалуйста - на рекламе изображённой над текстом (проспекте музея истори религии) и на других изображениях мандалы - это я один вижу - не абстрактный рисунок мироздания, а конкретный план - схему - чертёж?
И не просто чертёж, а чертёж механизма с ортогональной конической передачей - точнее редуктора с ортогональной конической передачей... да еще соединённый с ваджрой? ...или это у меня бред и когнитивный диссонанс?
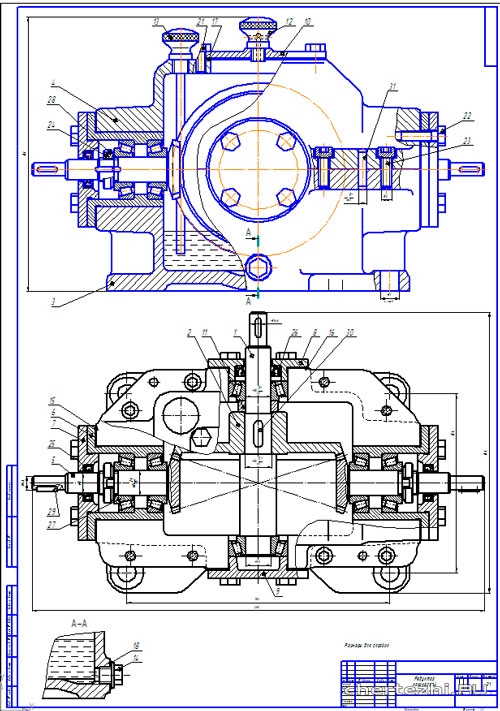



Конические зубчатые колеса. Оси конических колес зубчатой передачи составляют прямой угол, и их зубья обычно нарезаются по радиусам. Если зубья конических колес прямые, но идут не по радиусам, то они называются тангенциальными. Конические зубчатые передачи, оси колес которых не пересекаются, называются гипоидными. Их часто применяют в задних мостах автомобилей для понижения центра тяжести. В дифференциалах автомобилей применяются ортогональные зубчатые передачи с зубчатыми колесами одного диаметра. Спиральнозубые колеса подобны цилиндрическим, но их зубья нарезаются таким образом, что они передают вращение между взаимно перпендикулярными валами.
Конические зубчатые колеса применяют в передачах между валами, оси которых расположены под углом. Основное применение имеют передачи с пересекающимися под углом 90° осями, т. е. ортогональные передачи, которые рассматриваются ниже. Передачи с межосевым углом, не равным 90°, применяют редко из-за сложности форм и технологии изготовления корпусных деталей, несущих эти передачи, хотя для изготовления самих колес межосевой угол передачи не имеет значения. Пересечение осей валов затрудняет размещение опор. Одно из конических колес, как правило, располагают консольно. При этом увеличивается неравномерность распределения нагрузки по длине зуба. В коническом зацеплении действуют осевые силы, наличие которых усложняет конструкцию опор. Все это приводит к тому, что по опытным данным нагрузочная способность конической прямозубой передачи составляет лишь около 0,85 цилиндрической. Несмотря на отмеченные недостатки, а также то, что конические колеса сложнее, чем цилиндрические в изготовлении и монтаже, конические передачи имеют, широкое применение, поскольку по условиям компоновки механизмов довольно часто необходимо располагать валы под углом. Конические колеса выполняют с прямыми, тангенциальными, круговыми и другими криволинейными зубьями.
Прямозубые конические колеса следует применять при невысоких окружных скоростях (до 2...3 м/с) как наиболее простые в монтаже (допустимо до 8 м/с). При более высоких скоростях целесообразно применять колеса с круговыми зубьями, как обеспечивающие более плавное зацепление, меньший шум, большую несущую способность и более технологичные. Зубья обрабатывают на специальных станках для нарезания конических колес. В массовом и крупносерийном производстве в связи с возможностью компенсации при нарезании зубьев последующих закалочных деформаций конические колеса не шлифуют, а ограничиваются притиркой. В конических передачах для обеспечения при сборке правильного контакта зубьев предусматривают возможность осевой регулировки зубчатых колес. Несущая способность конических зубчатых передач с повышенным перекосом осей (от консольного расположения, недостаточной жесткости валов и корпусов) может быть несколько повышена даже по сравнению с передачами, имеющими круговой зуб, выполнением зубьев двояковыпуклыми и вогнутыми. Обе стороны зуба шестерни нарезают выпуклыми, а колеса - вогнутыми. Выигрыш получается вследствие того, что удельная жесткость пары зубьев не меняется по длине зубьев и пятно контакта при деформации валов не смещается.
http://any-book.org/download/28296.html
http://chertezhi.ru/modules/files/showfile.php?lid=16527
ваджра

Ма́ндала (санскр. मण्डल - круг, диск; тиб. དཀྱིལ་འཁོར, Вайли dkyil 'khor; монг. мандал) - сакральное схематическое изображение либо конструкция, используемая в буддийских и индуистских религиозных практиках.
http://ru.wikipedia.org/wiki/%CC%E0%ED%E4%E0%EB%E0

Мандала - это символ колеса жизни и смерти, космических процессов существования, планет и звезд, земных сезонов и галактических циклов.

МАНДАЛА (др.-инд. «mándala», «круг», «диск», «круглый», «круговой» и т. п.), один из основных сакральных символов в буддийской мифологии; ритуальный предмет, воплощающий символ; вид ритуального подношения (включая и жертву).
Замечательной чертой храмового (а также светского) строительства в Индии является то, что все индуистские храмы возводились по одному и тому же «строительному плану», который назывался Vāstu-purusa-mandala. Это слово толкуется следующим образом: «мандала» означает «план, схема, ритуальная диаграмма»; Пуруша - это космический человек, воплощающий в себе универсальное Бытие, начало, наполнение и суть всего (см. гимн в его честь в «Ригведе», X, 90); «васту» означает «место, вместилище». Таким образом, « Васту-пуруша-мандала» - не что иное, как «диаграмма местопребывания Пуруши», или план Космоса, воплощаемый на земле в виде храма, или образ Пуруши, его подобие. Итак, форма любого индуистского храма, его смысл и значение определяются этим планом-космограммой, регулируются им (существовали и другие виды мандал. Но это - символический план, а не план реального храма и не план местности, где он строился.
Архитектор (стхапати), строивший храм, должен был обладать, кроме архитектурной техники, знаниями всей философско-религиозной традиции, воплощаемой в создании мандалы: ведь строительство храмов в очень большой степени было связано с наблюдениями за небесными светилами, астрологией и астрономией, со сложными ритуалами («Манусамхита», VII, 47-48). Каждое движение при натягивании шнура и черчении линий мандалы на месте будущего храма было ритуальным и космически значимым. Вот почему это искусство рано нашло свое отражение в ведической литературе. В частности, традиционной архитектуре были посвящены специальные пособия - Vāstu-śāstras.
Как же выглядит строительная мандала? Это прежде всего квадрат в плане, ориентированный по странам света, и таковы все индуистские храмы, это их фундаментальная форма Мандала может быть выгравирована на камне или на алтаре, ее чертили на земле перед строительством храма в натуральную величину или же символически. По мнению Крамриш, квадрат предполагает круг и его в конечном итоге продуцирует; круг и квадрат координируют друг с другом в архитектуре Индии, начиная с ведического огненного алтаря Агни.
http://www.sunhome.ru/journal/51229

Скажите пожалуйста - на рекламе изображённой над текстом (проспекте музея истори религии) и на других изображениях мандалы - это я один вижу - не абстрактный рисунок мироздания, а конкретный план - схему - чертёж?
И не просто чертёж, а чертёж механизма с ортогональной конической передачей - точнее редуктора с ортогональной конической передачей... да еще соединённый с ваджрой? ...или это у меня бред и когнитивный диссонанс?




Конические зубчатые колеса. Оси конических колес зубчатой передачи составляют прямой угол, и их зубья обычно нарезаются по радиусам. Если зубья конических колес прямые, но идут не по радиусам, то они называются тангенциальными. Конические зубчатые передачи, оси колес которых не пересекаются, называются гипоидными. Их часто применяют в задних мостах автомобилей для понижения центра тяжести. В дифференциалах автомобилей применяются ортогональные зубчатые передачи с зубчатыми колесами одного диаметра. Спиральнозубые колеса подобны цилиндрическим, но их зубья нарезаются таким образом, что они передают вращение между взаимно перпендикулярными валами.
Конические зубчатые колеса применяют в передачах между валами, оси которых расположены под углом. Основное применение имеют передачи с пересекающимися под углом 90° осями, т. е. ортогональные передачи, которые рассматриваются ниже. Передачи с межосевым углом, не равным 90°, применяют редко из-за сложности форм и технологии изготовления корпусных деталей, несущих эти передачи, хотя для изготовления самих колес межосевой угол передачи не имеет значения. Пересечение осей валов затрудняет размещение опор. Одно из конических колес, как правило, располагают консольно. При этом увеличивается неравномерность распределения нагрузки по длине зуба. В коническом зацеплении действуют осевые силы, наличие которых усложняет конструкцию опор. Все это приводит к тому, что по опытным данным нагрузочная способность конической прямозубой передачи составляет лишь около 0,85 цилиндрической. Несмотря на отмеченные недостатки, а также то, что конические колеса сложнее, чем цилиндрические в изготовлении и монтаже, конические передачи имеют, широкое применение, поскольку по условиям компоновки механизмов довольно часто необходимо располагать валы под углом. Конические колеса выполняют с прямыми, тангенциальными, круговыми и другими криволинейными зубьями.
Прямозубые конические колеса следует применять при невысоких окружных скоростях (до 2...3 м/с) как наиболее простые в монтаже (допустимо до 8 м/с). При более высоких скоростях целесообразно применять колеса с круговыми зубьями, как обеспечивающие более плавное зацепление, меньший шум, большую несущую способность и более технологичные. Зубья обрабатывают на специальных станках для нарезания конических колес. В массовом и крупносерийном производстве в связи с возможностью компенсации при нарезании зубьев последующих закалочных деформаций конические колеса не шлифуют, а ограничиваются притиркой. В конических передачах для обеспечения при сборке правильного контакта зубьев предусматривают возможность осевой регулировки зубчатых колес. Несущая способность конических зубчатых передач с повышенным перекосом осей (от консольного расположения, недостаточной жесткости валов и корпусов) может быть несколько повышена даже по сравнению с передачами, имеющими круговой зуб, выполнением зубьев двояковыпуклыми и вогнутыми. Обе стороны зуба шестерни нарезают выпуклыми, а колеса - вогнутыми. Выигрыш получается вследствие того, что удельная жесткость пары зубьев не меняется по длине зубьев и пятно контакта при деформации валов не смещается.
http://any-book.org/download/28296.html
http://chertezhi.ru/modules/files/showfile.php?lid=16527
ваджра
