шедевры олимпиадной математики 2
В личную почту поступило решение предыдущей задачи, причём оно лучше чем то, которое я знал. Об этом чуть позже, а вот следующий шедевр.
Докажите, что в выпуклом шестиугольнике найдётся точка, сумма расстояний от которой до прямых, содержащих стороны, не превосходит суммы длин трёх средних линий (средняя линия это отрезок между серединами "противоположных" сторон).
Автор Наири Седракян, была на Туймааде в 2008 году.
Проведем главные диагонали. Они образуют треугольник. Рассмотрим точку пересечения его биссектрис. Она подойдёт, потому что если одну биссектрису продлить до сторон, то полученный отрезок короче средней линии. Поскольку средняя линия, на него проектируясь, покрывает его целиком.
Это рассуждение неплохое, но оно по существу евклидово. Ваня Митрофанов предложил более сложный аргумент, который зато работает в любой норме.
Попробуем выбрать в качестве такой точки одну из точек пересечения двух средних линий.
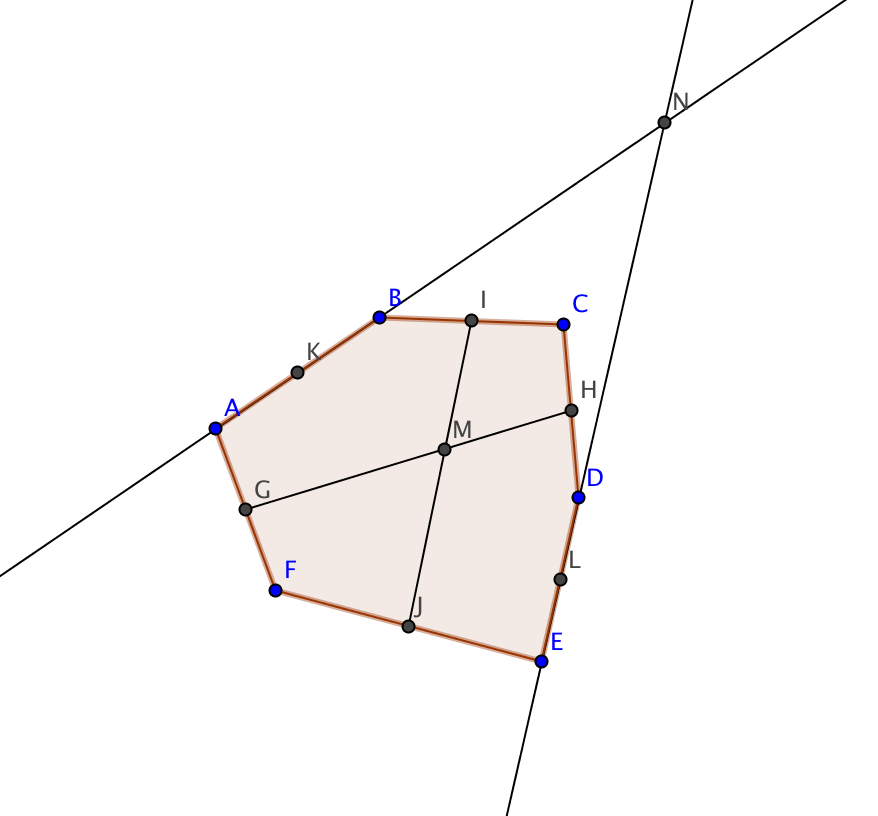
Вот эту точку M на картинке. Если она лежит в треугольнике KLN, то сумма расстояний до каждой пары противоположных сторон не превосходит соответствующей средней линии (для средней линии KL это следует из того, что длина отрезка, проведенного через M параллельно KL до прямых AB,DE короче чем KL). Итак, точка M лежит вне треугольника KLN, аналогично для двух других точек пересечения средних линий. Но это невозможно. Доказать это можно, например, так.
Средняя линия IJ есть геометрическое место таких точек X, что |XBF|-|XCE|=(|CBF|-|CBE|)/2=(|EBF|-|CFE|)/2, где |XYZ| обозначает ориентированную площадь треугольника, ориентация выбрана так, что на отрезке IJ площади положительны. Аналогично для других средних линий.
Выберем точку T в треугольнике, образованном средними линиями (можно взять одну из его вершин). Условие, что точка M лежит вне треугольника KLN означает, что знаки f(T)<0, где f(X)=|XAE|-|XBD|-(|BAE|-|ABD|)/2 (знак именно такой, поскольку f(A)<0 и точки A,T по одну сторону от KL). Складывая все такие неравенства и неравенства типа |BDE|<|ADE| получаем после некоторой работы противоречие.
Докажите, что в выпуклом шестиугольнике найдётся точка, сумма расстояний от которой до прямых, содержащих стороны, не превосходит суммы длин трёх средних линий (средняя линия это отрезок между серединами "противоположных" сторон).
Автор Наири Седракян, была на Туймааде в 2008 году.
Проведем главные диагонали. Они образуют треугольник. Рассмотрим точку пересечения его биссектрис. Она подойдёт, потому что если одну биссектрису продлить до сторон, то полученный отрезок короче средней линии. Поскольку средняя линия, на него проектируясь, покрывает его целиком.
Это рассуждение неплохое, но оно по существу евклидово. Ваня Митрофанов предложил более сложный аргумент, который зато работает в любой норме.
Попробуем выбрать в качестве такой точки одну из точек пересечения двух средних линий.

Вот эту точку M на картинке. Если она лежит в треугольнике KLN, то сумма расстояний до каждой пары противоположных сторон не превосходит соответствующей средней линии (для средней линии KL это следует из того, что длина отрезка, проведенного через M параллельно KL до прямых AB,DE короче чем KL). Итак, точка M лежит вне треугольника KLN, аналогично для двух других точек пересечения средних линий. Но это невозможно. Доказать это можно, например, так.
Средняя линия IJ есть геометрическое место таких точек X, что |XBF|-|XCE|=(|CBF|-|CBE|)/2=(|EBF|-|CFE|)/2, где |XYZ| обозначает ориентированную площадь треугольника, ориентация выбрана так, что на отрезке IJ площади положительны. Аналогично для других средних линий.
Выберем точку T в треугольнике, образованном средними линиями (можно взять одну из его вершин). Условие, что точка M лежит вне треугольника KLN означает, что знаки f(T)<0, где f(X)=|XAE|-|XBD|-(|BAE|-|ABD|)/2 (знак именно такой, поскольку f(A)<0 и точки A,T по одну сторону от KL). Складывая все такие неравенства и неравенства типа |BDE|<|ADE| получаем после некоторой работы противоречие.