Как растут листья на деревьях?
27 июня 2016
Невзирая на кажущийся хаос и беспорядочность, у большинства растений листья располагаются на стеблях и ветвях настолько правильно, что можно установить касательно их расположения общие правила.
При поверхностном наблюдении кажется, будто чаще всего листья расположены без всякого порядка, что они разбросаны, как говорится и до сих пор в большей части описательных сочинений (folia sparsa). Только у тех растений, у которых каждый стеблевой узел несет больше одного листа, правильность листорасположения бросается в глаза и давно замечена. Если листья сидят попарно и один против другого, то про них справедливо выражаются, что они противоположные, или супротивные (folia opposita).
При этом бывает почти всегда, что листовые пары между собой чередуются - тогда листья ближайших пар приходятся друг к другу накрест, листья третьей пары, считая снизу, приходятся прямо над листьями первой пары, листья 4-й над листьями 2-й и т. д. Для обозначения этого обстоятельства употребляется выражение накрест сидящие (f. f. decussata). Так бывает, напр., у наших кленов, у сирени, у всех губоцветных (мята, шалфей и пр.). Вместо двух листьев на одном узле бывает 3 листа, напр. у олеандра, и тогда ближайшие листья таких тройных колец или кружков тоже между собою чередуются; известны и такие растения, у которых на каждом узле бывает 4, 6, 10 и даже больше листьев (многие мареновые, Hippuris и пр.).
Но и в этих случаях листья ближайших кружков чередуются. Такие листья можно называть кольчаторасположенными, или кольчатыми (f. f. verticillata). Парные и противоположные, очевидно, относятся сюда же, только число листьев в их кружках доведено до наименьшего. Если на стеблях с кольчаторасположенными листьями мысленно соединить все листья, друг над другом сидящие, то получится несколько вертикальных и параллельных между собою линий, которые называются ортостихами. Число таких ортостих будет, очевидно, вдвое больше числа листьев в данном кружке. Правильность, отсюда происходящая, до того ясна, что, напр., у растений с противоположными листьями, особенно, если листьев много, их четыре ортостиха видны при первом взгляде. Разбросанные листья представляют правильность другого рода. Стебли и ветви с такими листьями производят по одному листу на каждом узле.
Если мы, начиная от любого листа, напр. от самого нижнего, проведем мысленно линию к ближайшему листу, а от второго опять к ближайшему и т. д. до конца, то линия эта окажется винтовою, а на горизонтальной проекции спиральною. Поэтому и самое Л. называется спиральным, листья - спиральнорасположенными (f. f. spiraliter posita).
При этом оказывается следующее. Идя по спирали, напр. кверху от данного листа, мы доходим до такого, который приходится над первым (с которого начали). У одних растений, как у липы, этот лист всегда 3-й, над 2-м приходится 4-й, над 3-м 5-й и т. д.; у других, как у ольхи, над 1-м приходится 4-й, над 2-м - 5-й и т. д.; у третьих, напр. у осины, над 1-м приходится 6-й, над 2-м - 7-й и т. д. Если провести вертикальные линии через все взаимно прикрывающиеся листья, то число их будет равно числу листьев, расположенных между двумя взаимно прикрывающимися листьями: у липы 2-м, у ольхи - 3-м, у осины - 5.
Если измерить горизонтальное расстояние между ортостихами, то оно окажется постоянным у каждого растения и будет равно отрезку спирали, соединяющему 2 взаимно прикрывающиеся листа. Отрезок этот называется полным циклом листорасположения. У одних растений (липа, ольха) он совершает один оборот вокруг стебля, у других (осина, тополь, яблоня) совершает 2 оборота, у третьих (Carduus) - 3 оборота и т. д. Расстояние это, измеряемое дугой и соответствующим ей углом, между двумя ближайшими листьями называется расхождением (divergentia) листьев, а угол, измеряющий величину расхождения, - углом расхождения (angulus divergentiae).
Ясно, что этот угол зависит от числа оборотов в полном цикле и от числа листьев, расположенных по линии полного цикла. Если оборот один, т. е. один круг, а листьев в цикле 2, то для отыскания угла расхождения требуется разделить круг надвое, получится угол расхождения в 1/2, где 1 означает число оборотов в цикле, а 2 - число расположенных на нем листьев; если число листьев 3, то круг делится на 3, получается расхождение в 1/3, если число оборотов 2 (т. е. 2 круга), а листьев 5, то эти 2 круга следует, очевидно, разделить на 5, получится расхождение в 2/5, где 2 означает опять число оборотов, а 5 - число листьев цикла.
Исследуя множество растений, найдено, что в природе имеются весьма различные расхождения, но чаще всего в природе попадаются следующие: 1/2, 1/3, 2/5, 3/8, 5/13, 8/21 и т. д., но из них самые распространенные первые три. Каждая из этих дробей, означая расхождение, вместе с тем, очевидно, означает и самое Л., указывая в знаменателе на число листьев в цикле и на число вертикальных рядов (ортостих), ими образуемых, а в числителе - число оборотов спирали в полном цикле.
Поэтому каждое листорасположение может означаться числом листовых рядов, или ортостих: они называются двурядными (1/2), трехрядными (1/3) и т. д. В природе, однако же, кроме тех дивергенций, что указаны в вышеприведенном ряде дробей, называемом главным, так как он гораздо чаще других попадается, имеются и другие ряды, напр. 1/3, 1/4, 2/7 и т. д. или 1/4, 1/5, 2/9 и т. д. Во всех этих рядах расхождений замечается, что каждая последующая дробь получается с помощью сложения числителей и знаменателей двух предыдущих, что, впрочем, не указывает на какую-либо законность в самой природе растений.
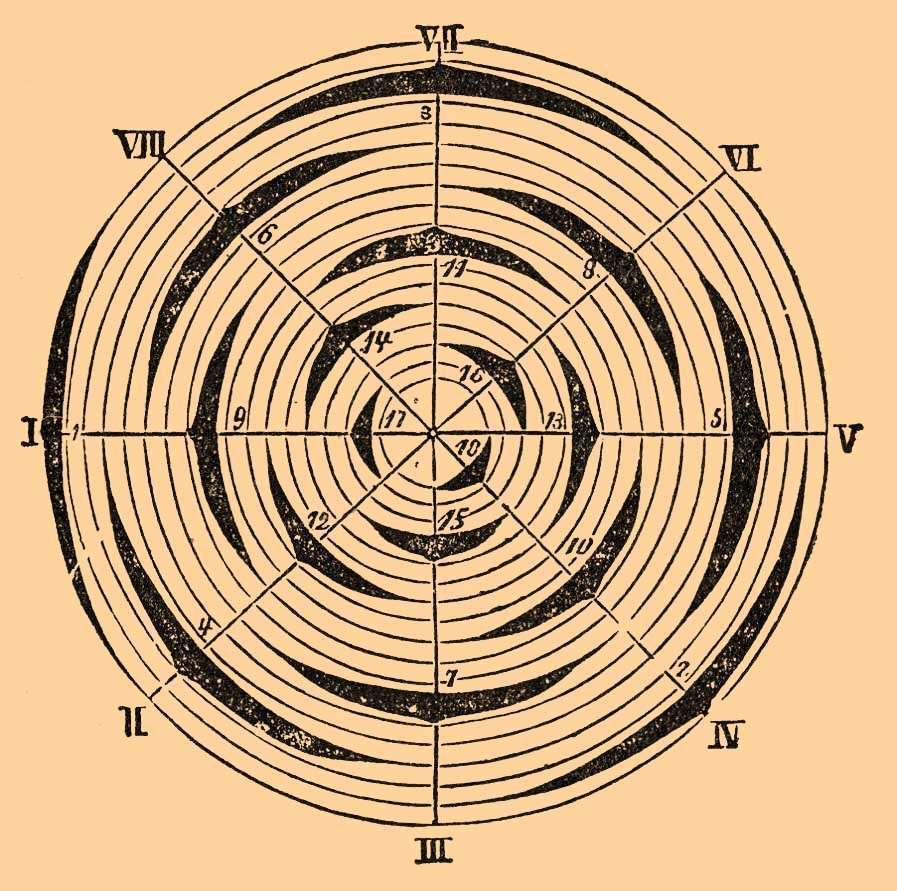
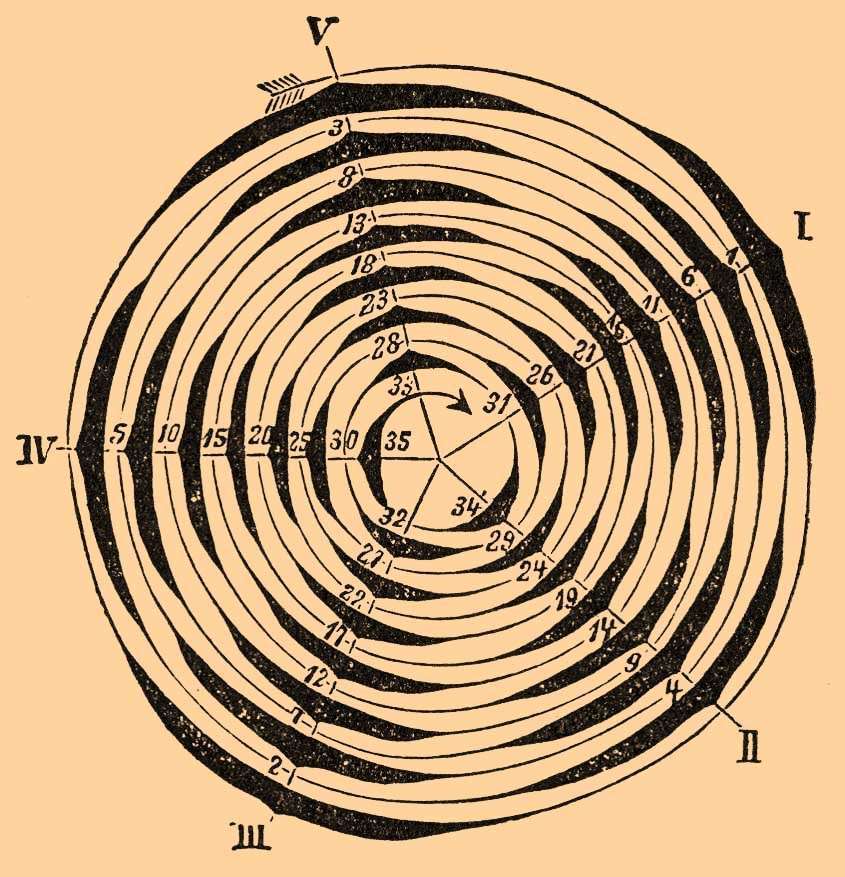
Для наглядного представления Л. удобно представлять их на горизонтальной проекции, получаемой при мысленном проведении вертикалей из точек прикрепления листьев при вертикальном положении самого лиственного стебля. Точки пересечения вертикалей (перпендикуляров) с горизонтальною плоскостью, очевидно, расположатся так же, как расположены листья на стебле. Вместо точек чертят обыкновенно дуги, означающие листья (их поперечный разрез), утолщая дуги в тех местах, где на проекции получились точки, т. е. на середине каждой дуги. Такой чертеж представляет собою план листвоносного побега, так как в середине его чертится круг, означающий поперечный разрез самого стебля. План этот есть диаграмма листоносного побега. На диаграммах очевидно число листьев цикла, их взаимное расположение и угол расхождения.
Они употребляются больше всего при изучении соцветий и цветов. Правильность расположения листьев, хотя и наблюдается у большинства растений, но известны исключения, т. е. такие растения, у которых расхождение не постоянно. Кроме того, расхождение нередко меняется при переходе от главного стебля к ветвям, что, впрочем, совершается всегда на один и тот же лад. Необходимо еще заметить, что у многих растений ряды взаимно прикрывающихся листьев, хотя и остаются параллельными, но представляются не вертикальными, а кривыми. В каждом многочленном Л. можно всегда открыть, кроме той главной винтовой линии, или спирали, которая проходит через все листья побега, еще второстепенные, более крутые спирали, направляющиеся в 2 противоположные стороны.
Эти второстепенные спирали называются парастихами. Парастихи одного направления, вместе взятые, захватывают, очевидно, также все листья побега, но каждая из них лишь известную их часть, а именно 1/2 всех листьев, если одноименных парастих 2, одну треть - если их три и т. д., что уже следует из того обстоятельства, что они параллельны и захватывают все листья побега. Если главная спираль очень полога и ее незаметно, как то бывает на побегах с весьма многочисленными Л., то парастихами пользуются для открытия главной спирали. Для этого нужно перенумеровать все листья на парастихах того и другого направления, начиная от любого, наблюдая при том, чтобы между номерами была разность, равная числу парастих.
После перенумерования всех парастих главная спираль оказывается сама собой. Правильность в расположении листьев, открываемая и изображаемая помощью выше представленного способа, находится в ближайшей связи с развитием и внутренним строением растений, она также соответствует необходимости приспособления растений к окружающим условиям, но физиологического объяснения тут еще не найдено.
Исследования Негели, Гофмейстера и Швенденера показали, что во многих случаях Л. в начале развития побега, когда листья имеют вид маленьких бугорков, иное, чем по окончании развития. Последний из названных ученых показал также, что вследствие более медленного роста несущего листья побега по сравнению с ростом самих листьев листья претерпевают взаимное давление, смещаются по определенным направлениям и меняют свое положение, располагаясь по известной формуле окончательно только при завершении своего развития.
Эти исследования, объясняя еще и прежде замеченное различие между расположением листьев в начале и в конце, не дают, однако же, полного механического объяснения, так как во многих случаях, напр. на побегах с противоположными листьями, листья эти располагаются с самого начала так же, как они расположены в конце. Основательным изучением и самою формуляцией Л. наука обязана всего более Александру Брауну, Шимперу и братьям Браве.
Литература. A. Braun, "Vergleichende Untersuchung ueber die Ordnung der Schuppen an der Tannenzapfen" ("Abhandlungen der Leopoldinisch-K arolinischen Akademie", т. 14); L. F. et A. Bravais, "Essai sur la disposition des feuilles curvis érié es" ("An. d. sc. nat.", 1837, т. 7); они же, "Essai sur la disposition des feuilles rectis érié es" ("An. des sc. nat.", 1838); С. Schimper, "Ueber die M öeglichkeit eines Wissenschaftlichen Verstä ndnisses der Blatt-Stellung, mitgetheilt von A. Braun" ("Flora", 1835, №№ 10, 11 и 12); Simon Schwendener, "Mechanische Theorie der Blattstellungen" (Лпц., 1878).
А. Бекетов
Постоянный адрес статьи: http://xn--b1amnebsh.ru-an.info/новости/как-растут-листья-на-деревьях/