Почему микроэлектроника не сводится к гонке за нанометрами

Почему микроэлектроника не сводится к гонке за нанометрами
Юрий Панчул, Саннивейл, Калифорния, апрель-май 2013
1. Введение
Господа! В нескольких ветках предыдущего поста возникла дискуссия, сводится ли микроэлектроника к гонке за нанометрами.
Ответ на этот вопрос не менее архиважен для будущего России, чем судьба Пусси Райотс.
Ведь если микроэлектроника сводится к гонке за нанометрами, то российским микроэлетронщикам нечего ловить. Все, что им остается в жизни - это слушать оппозиционные рок-песни, наблюдая за клином протестантских журавлей в небе. Ибо Интел "держит самый маленький нанометр за яйца", а коварный Госдеп следит чтобы россияне всегда отставали от передового нанометра минимум на два поколения. (Иными словами, правительство США ограничивает technology transfer за рубеж для самых новых технологий, в исследованиях и разработке которых использовались какие-либо гранты от американского правительства).
К счастью, микроэлектроника НЕ сводится к гонке за нанометром, и российским разработчиками микросхем ЕСТЬ что ловить. В частности, они могут создавать прибавочную стоимость за счет выдумывания более хитрой микроархитектуры специализированных IP-блоков и лицензирования оных международным компаниям.
Цель данного поста - показать, насколько широко можно варьировать в хардвере даже такую казалось бы простую операцию, как взятие квадратного корня, причем все вариации будут протекать без изменения нанометра. Но сначала сделаем небольшое отступление.

2. Отступление. Архитектура и микроархитектура - два большие разницы.
Вопрос микроархитектуры вызывает замешательство у трех групп людей, спорящих о вопросе:
1. У Юлии Латыниной, also known as "стрелка осциллографа".
2. У чистых программистов, которые рассматривают процессор как черный ящик.
3. У чистых физиков, которые видят на уровне транзистора.
Чистым програмистам при слове "микроархитектура" мерещится либо архитектура, либо многоядерность, либо выплывшее из какой-то старой книжки смутное слово "микрокод". А чисто физическое видение мира иногда передается даже некоторым программистам, которые специализируются на EDA-тулах физического уровня (EDA = Electronic Design Automation).
Поэтому введем понятия архитектуры и микроархитектуры.
Архитектура процессора - это то, как процессор выглядит для программиста. В нее входит система команд, видимая программисту организация памяти и видимых программисту регистров.
Микроархитектура процессора - это то, как процессор выглядит для разработчика логики (но не физики) процессора. В нее входит организация конвейера, алгоритм предсказателя перехода, такие трюки как forwarding, register renaming и т.д.
Одна из главных целей хардверного инженера на уровне логики / разработчика микроархитектуры - поддержать иллюзию простого последовательного выполнения команд для софтверного инженера / пользователя архитектуры, начиная от программиста на ассемблере. Т.е. реально в процессоре инструкции могу выполняться спекулятивно, отменяться перед самым завершением и т.д., но программист этого никогда не увидит, хотя с помощью тонких измерений может заметить флуктуации скорости и различия при сценариях работы с общей памятью в многопроцессорных сиcтемах.
Аналогия: Архитектура - техника вождения автомобиля (что происходит при нажатии на газ, тормоз, повороте руля), микроархитектура - как устроен автомобиль (двигатель, трансмиссия, соединения и т.д.).
С этим все. Теперь:
3. Разъяснение на пальцах концепций комбинационной (combinational), секвенциальной (sequential) и конвейерной (pipelined) организации вычислений
Представьте, что вам нужно организовать работу медкомиссии военкомата. Это можно сделать несколькими способами, в зависимости от поставленных целей.
Если целью является минимизация количества помещений для осмотра, то можно усадить всех членов комиссии в одну большую комнату, в которую впускать по одному. Это пример комбинационной (combinational) организации вычислений. Недостатком его будет то, что осмотр каждого допризывника будет проходить долго, а члены комиссии будут скучать.

Если целью является минимизация количества специалистов, то можно устроить и так, но при этом у военкоматовца-одиночки должно быть несколько специальностей (глазник, зубник, уролог), и нужно будет нанять специального товарища, который бы временно выводил допризывника из комнаты, пока военкоматовец меняет в ней оборудование - вещает табличку проверки зрения на стену, ставит зубоврачебное кресло (обстановка, определяемая состоянием конечного автомата, state). А потом помощник по звоночку (тактовому сигналу, clock) вводил бы допризывника обратно для следущей стадии осмотра.
Это пример секвенциальной (sequential) организации вычислений. Частным случаем такой организации вычислений является популярный в 1970-х годах микрокод - трюк, который я не буду рассматривать в данном посте.

Наконец, если у вас есть много комнат, то можно организовать конвейер (pipeline), который будет обеспечивать наибольшую пропускную способность, в идеальном случае определяемую только одним (самым медленным) специалистом. В неидеальном случае допризывник может начать скандалить и затормозит процесс для всех (stall) или для всех. кто стоит за ним (slip). Против этого существуют всякие out-of-order методы, которые я не буду рассматривать в этом посте - наш "военкомат" (конвейер для квадратного корня) будет работать идеально.

4. Проиллюстрируем наши рассуждения кодом и мигающими лампочками
Для иллюстрации я не буду использовать конвейерный процессор, а возьму нечто гораздо более базовое, а именно покажу свою реализацию несколькими способами хардвера для вычисления целочисленного квадратного корня. Я выложил весь код на https://code.google.com/p/fpga-examples/source/browse/trunk/showroom/isqrt/
Если вы никогда не слышали слова "верилог", "синтез", "симуляция", то я рекомендую вам для начала прочитать мой пост в ru_programming
http://ru-programming.livejournal.com/1271886.html
Введение в дизайн харвера микросхем для тех программистов, которые этим никогда не занимались

Хотя существует куча книжек про хардверную имплементацию компьютерной арифметики для хардверных дизайнеров, я взял исходный алгоритм квадратного корня из софтверной книжки, которая называется "Восторг хакера", а потом его переделал его под хардвер. Почему "Восторг хакера"? Частично чтобы показать, как переделывать софтверные алгоритмы в хардвер, а частично потому, что первое издание этой книги просто валялось у меня под рукой. Вот второе издание:
Hacker's Delight (2nd Edition) by Henry S. Warren
http://www.amazon.com/Hackers-Delight-Edition-Henry-Warren/dp/0321842685
Софтверный код из книжки Генри Воррена "Восторг хакера" выглядит вот так, я скопировал его с косметическими изменениями как отправную точку для последующих преобразований:
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/001_software_implementation/isqrt.c
unsigned isqrt (unsigned x)
{
unsigned m, y, b;
m = 0x40000000;
y = 0;
while (m != 0) // Do 16 times
{
b = y | m;
y >>= 1;
if (x >= b)
{
x -= b;
y |= m;
}
m >>= 2;
}
return y;
}
Вот мой тестик для данной функции, чтобы вы не сомневались, что она работает: http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/001_software_implementation/test.c
5. Комбинационная имплементация
Из кода книжки Воррена легко сварганить "наивную" имплементацию на Верилоге, которая будет работать (симулироваться, синтезироваться), но при виде которой хардверные инженеры будут от вас шарахаться. Дело в том, что "repeat" - это не так сказать компактный цикл в софтверной парадигме, а фактически "препроцессорная" директива скопировать код внутри него 16 раз:
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/002_combinational_unstructured/isqrt.v
// combinational unstructured
module isqrt
(
input [31:0] x,
output reg [15:0] y
);
reg [31:0] m, tx, ty, b;
always @*
begin
m = 31'h4000_0000;
tx = x;
ty = 0;
repeat (16)
begin
b = ty | m;
ty = ty >> 1;
if (tx >= b)
begin
tx = tx - b;
ty = ty | m;
end
m = m >> 2;
end
y = ty [15:0];
end
endmodule
Эта комбинационная (combinational) имплементация. Протокол общения с ней очень прост - нужно положить число на вход x, и через довольно длинное по хардверным меркам время (типа 100 наносекунд на Altera Cyclone II FPGA) на выходе появится правильное значение. Все эти томительные 100 наносекунд комбинаторная логика внутри дизайна будет чавкать и булькать вдоль довольно длинного combinational path, пока не прийдет в стабильное состояние. Вот фрагмент этого пути:
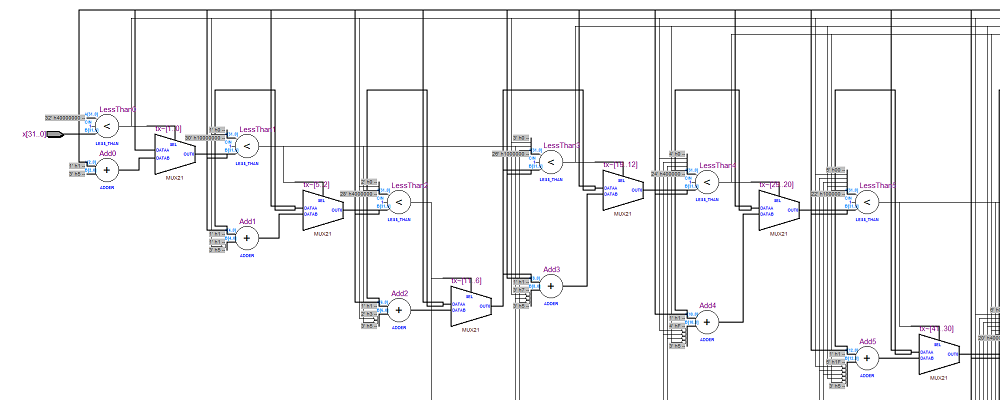
6. Секвенциальная имплементация
Количество логики можно сильно уменьшить, если имплементировать только одну итерацию цикла, с одним сумматором и компаратором, но прогнать через него временные значения x и y шестнадцать раз. Для того, чтобы железо (косная материя) поняла недвусмысленно, что бы хотите делать чего-нибудь итеративно, вам прийдется ввести концепцию тактового сигнала (clock) и импементировать фактически небольшой конечный автомат.
Иными словами построить секвенциальную (sequential) имплементацию:
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/003_sequential/isqrt.v
// sequential
module isqrt
(
input clock,
input reset_n,
input run,
input [31:0] x,
output reg ready,
output reg [15:0] y
);
reg [31:0] m, r_m;
reg [31:0] tx, r_tx;
reg [31:0] ty, r_ty;
reg [31:0] b, r_b;
reg new_ready;
always @*
begin
if (run)
begin
m = 31'h4000_0000;
tx = x;
ty = 0;
end
else
begin
m = r_m;
tx = r_tx;
ty = r_ty;
end
b = ty | m;
ty = ty >> 1;
if (tx >= b)
begin
tx = tx - b;
ty = ty | m;
end
new_ready = m [0];
m = m >> 2;
end
always @(posedge clock or negedge reset_n)
begin
if (! reset_n)
begin
ready <= 0;
y <= 0;
end
else if (new_ready)
begin
ready <= 1;
y <= ty [15:0];
end
else
begin
ready <= 0;
r_m <= m;
r_tx <= tx;
r_ty <= ty;
r_b <= b;
end
end
endmodule
7. Вопросы стиля при секвенциальной имплементации
У читателя моего блога, который начинает использовать Верилог, может появиться два вопроса:
1. А зачем делать два always-блока (combinational и clocked)? Почему бы не поместить все в один clocked always block? Ведь синтезатору все равно?
2. Почему все присваивания в combinational always block являются blocking, а все присваивания в clocked always block являются non-blocking?
Дело в том, что следование такому стилю позволяет решить две проблемы - неумышленные регистры (flip-flops) и race conditions.
Допустим человек хотел сделать временную переменную t, значение которой он не собирается сохранять между пульсами clock-а и собирался написать:
always @(posedge clock)
begin
t = a;
if (b)
t = b;
c <= t;
end
Теперь допустим, что человек забыл написать первое присваивание:
always @(posedge clock)
begin
if (b)
t = b;
c <= t;
end
Синтезатор может просто тихо сгенерировать флип-флоп, а человек заметит ошибку только когда дизайн уже будет выпекаться на фабрике на Тайване, после чего его работодателю прийдется потратить пару миллионов долларов на ликвидацию последствий (и слава Аллаху, если дизайн не пойдет в чип на АЭС!).
Вот такой стиль позволяет заметить ошибку рано, ибо синтезатор начнет ругаться про level-sensitive latch, и дизайнер будет всегда уверен, какие переменные в его дизайне являются настоящими регистрами, а какие - эфемерной фикцией:
always @*
begin
t = a;
if (b)
t = b;
end
always @(posedge clock)
c <= t;
Для сходных целей я отделяю реальные регистры префиксом r_ от временных переменных (tx и r_tx).
А почему все присваивания в clocked always block являются non-blocking? Чтобы избежать race conditions.
Пример race condition:
always @(posedge clock)
a = f (t);
always @(posedge clock)
t = b;
Понятно, что значение a будет зависеть от прихоти симулятора - будет ли сначала обработан первый always-блок или второй.
А вот если сделать все присваивания в clocked always block - non-blocking, то эта проблема исчезает - a будет вычислено строго на основе значения t до фронта тактового сигнала.
always @(posedge clock)
a <= f (t);
always @(posedge clock)
t <= b;
А почему все присваивания в combinational always block являются blocking? Для однородности, скорости симуляции (меньше дельта-циклов) и чтобы делать как выше (присваивать значение по умолчанию и потом его менять).
Этот дизайн можно гонять на довольно неплохой тактовой частоте - 123 MHz на Altera Cyclone II FPGA, т.е. каждый цикл будет занимать всего восемь с небольшим наносекунд. К сожалению, это не впечатляет, так как на вычисление каждого квадратного корня будет тратиться 16 циклов или в сумме более 130 наносекунд, что хуже, чем комбинационный квадратный корень.
Иными словами - у секвенциального дизайна меньше оборудования (комбинационных сумматоров и компараторов), но хуже общее время выполнения, чем у комбинационного квадратного корня.
Пропускную способность дизайна можно существенно повысить тремя способами:
1. Введением нескольких вычислителей квадратного корня, работающих параллельно (в рамках военкоматной аналогии - введение нескольких комиссий на военкомат)
2. Организацией конвейера
3. Введением передового нанометра (этот способ из-за происков Госдепа против россиян мы не рассматриваем)
8. Постепенно введем конвейерную имплементацию
Для организации конвейера все, что нам нужно - это структуризировать комбинационную имплементацию и вставить 16 слоев регистров, синхронизированных тактовым сигналом.
В рамках военкоматной аналогии - вывести комиссию из большой комнаты, рассадить их в 16 маленьких комнаток по одному специалисту в комнату и вместо долгого осмотра всей группой одного допризывника в большой комнате - направить каждого допризывника посетить все комнаты по очереди. Пока он дойдет по 16 комнаты, его 15 друзей будут параллельно с ним осматриваться в предыдущих комнатах на разных стадиях осмотра.
Пропускная способность может увеличиться не в 16 раз (так как во многих дизайнах стадии разные) но в несколько раз, за вычетом неравномерности скорости в разных стадиях и издержек (setup и hold time) на вход и выход из каждой комнаты.
Для начала структурируем нашу комбинационную имплементацию, чтобы она не шокировала людей.
Для начала сделаем подмодуль, который имплементирует комбинационную логику для одной итерации:
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/004_combinational_structured_no_generate/isqrt_slice.v
module isqrt_slice
(
input [31:0] ix,
input [31:0] iy,
output [31:0] ox,
output [31:0] oy
);
parameter [31:0] m = 32'h4000_0000;
wire [31:0] b = iy | m;
wire x_ge_b = ix >= b;
assign ox = x_ge_b ? ix - b : ix;
assign oy = (iy >> 1) | (x_ge_b ? m : 0);
endmodule
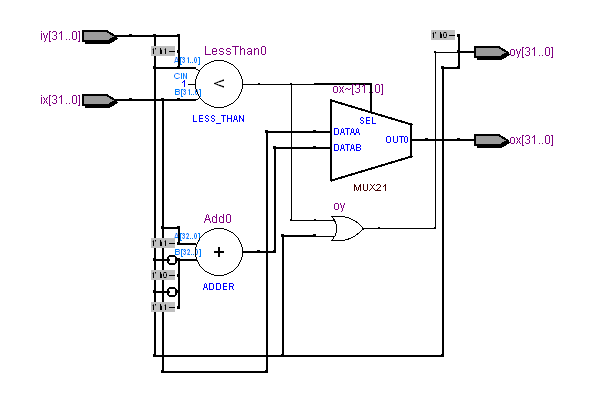
Теперь разобьем большой комбинационный модуль на такие подмодули:
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/004_combinational_structured_no_generate/isqrt.v
// combinational structured no generate
module isqrt
(
input [31:0] x,
output [15:0] y
);
localparam [31:0] m = 32'h4000_0000;
wire [31:0] wx [0:16], wy [0:16];
assign wx [0] = x;
assign wy [0] = 0;
isqrt_slice #(m >> 0 * 2) i00 (wx [ 0], wy [ 0], wx [ 1], wy [ 1]);
isqrt_slice #(m >> 1 * 2) i01 (wx [ 1], wy [ 1], wx [ 2], wy [ 2]);
isqrt_slice #(m >> 2 * 2) i02 (wx [ 2], wy [ 2], wx [ 3], wy [ 3]);
isqrt_slice #(m >> 3 * 2) i03 (wx [ 3], wy [ 3], wx [ 4], wy [ 4]);
isqrt_slice #(m >> 4 * 2) i04 (wx [ 4], wy [ 4], wx [ 5], wy [ 5]);
isqrt_slice #(m >> 5 * 2) i05 (wx [ 5], wy [ 5], wx [ 6], wy [ 6]);
isqrt_slice #(m >> 6 * 2) i06 (wx [ 6], wy [ 6], wx [ 7], wy [ 7]);
isqrt_slice #(m >> 7 * 2) i07 (wx [ 7], wy [ 7], wx [ 8], wy [ 8]);
isqrt_slice #(m >> 8 * 2) i08 (wx [ 8], wy [ 8], wx [ 9], wy [ 9]);
isqrt_slice #(m >> 9 * 2) i09 (wx [ 9], wy [ 9], wx [10], wy [10]);
isqrt_slice #(m >> 10 * 2) i10 (wx [10], wy [10], wx [11], wy [11]);
isqrt_slice #(m >> 11 * 2) i11 (wx [11], wy [11], wx [12], wy [12]);
isqrt_slice #(m >> 12 * 2) i12 (wx [12], wy [12], wx [13], wy [13]);
isqrt_slice #(m >> 13 * 2) i13 (wx [13], wy [13], wx [14], wy [14]);
isqrt_slice #(m >> 14 * 2) i14 (wx [14], wy [14], wx [15], wy [15]);
isqrt_slice #(m >> 15 * 2) i15 (wx [15], wy [15], wx [16], wy [16]);
assign y = wy [16];
endmodule


У такого описания есть несколько проблем стиля, которые OK для небольших дизайнов, но которые могут превратиться в большие проблемы, когда количество cтрочек кода меряется в сотни тысяч.
В частности, не рекомендуется использовать разные элементы одного и того же массива из wires для подсоединения к вводу и выводу в рамках одной и той же instantiation.
И особенно не рекомендуется подсоединение к портам по позиции, а не по имени. То же относится к параметрам модулей. Даже для небольших модулей лучше методически подсоединять по имени, т.е. писать не "f #(a) i (b, c)", а "f #(.a (a)) i (.b (b), .c (c))". Потому что потом кто-нибудь введет в модуль f дополнительный параметр или порт, а кто-нибудь другой перепутает порядок или не обратит внимание на warning с подсоединением по умолчанию.
В SystemVerilog введена конструкция для специального подсоединения по имени по умолчанию (".*"), но она может не поддерживаться бесплатными тулами от Xilinx и Altera, которые я рекомендую для читателей, не имеющих доступа к Synopsys, Cadence и полной версии Mentor.
Итого, более дисциплинированная все еще комбинационная версия:
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/005_combinational_structured_rigid_no_generate/isqrt.v
// combinational structured rigid no generate
module isqrt
(
input [31:0] x,
output [15:0] y
);
localparam [31:0] m = 32'h4000_0000;
wire [31:0] ix [0:15], iy [0:15];
wire [31:0] ox [0:15], oy [0:15];
isqrt_slice #(.m (m >> 0 * 2)) i00 (.ix (ix [ 0]), .iy (iy [ 0]), .ox (ox [ 0]), .oy (oy [ 0]));
isqrt_slice #(.m (m >> 1 * 2)) i01 (.ix (ix [ 1]), .iy (iy [ 1]), .ox (ox [ 1]), .oy (oy [ 1]));
isqrt_slice #(.m (m >> 2 * 2)) i02 (.ix (ix [ 2]), .iy (iy [ 2]), .ox (ox [ 2]), .oy (oy [ 2]));
isqrt_slice #(.m (m >> 3 * 2)) i03 (.ix (ix [ 3]), .iy (iy [ 3]), .ox (ox [ 3]), .oy (oy [ 3]));
isqrt_slice #(.m (m >> 4 * 2)) i04 (.ix (ix [ 4]), .iy (iy [ 4]), .ox (ox [ 4]), .oy (oy [ 4]));
isqrt_slice #(.m (m >> 5 * 2)) i05 (.ix (ix [ 5]), .iy (iy [ 5]), .ox (ox [ 5]), .oy (oy [ 5]));
isqrt_slice #(.m (m >> 6 * 2)) i06 (.ix (ix [ 6]), .iy (iy [ 6]), .ox (ox [ 6]), .oy (oy [ 6]));
isqrt_slice #(.m (m >> 7 * 2)) i07 (.ix (ix [ 7]), .iy (iy [ 7]), .ox (ox [ 7]), .oy (oy [ 7]));
isqrt_slice #(.m (m >> 8 * 2)) i08 (.ix (ix [ 8]), .iy (iy [ 8]), .ox (ox [ 8]), .oy (oy [ 8]));
isqrt_slice #(.m (m >> 9 * 2)) i09 (.ix (ix [ 9]), .iy (iy [ 9]), .ox (ox [ 9]), .oy (oy [ 9]));
isqrt_slice #(.m (m >> 10 * 2)) i10 (.ix (ix [10]), .iy (iy [10]), .ox (ox [10]), .oy (oy [10]));
isqrt_slice #(.m (m >> 11 * 2)) i11 (.ix (ix [11]), .iy (iy [11]), .ox (ox [11]), .oy (oy [11]));
isqrt_slice #(.m (m >> 12 * 2)) i12 (.ix (ix [12]), .iy (iy [12]), .ox (ox [12]), .oy (oy [12]));
isqrt_slice #(.m (m >> 13 * 2)) i13 (.ix (ix [13]), .iy (iy [13]), .ox (ox [13]), .oy (oy [13]));
isqrt_slice #(.m (m >> 14 * 2)) i14 (.ix (ix [14]), .iy (iy [14]), .ox (ox [14]), .oy (oy [14]));
isqrt_slice #(.m (m >> 15 * 2)) i15 (.ix (ix [15]), .iy (iy [15]), .ox (ox [15]), .oy (oy [15]));
assign ix [ 0] = x;
assign ix [ 1] = ox [ 0];
assign ix [ 2] = ox [ 1];
assign ix [ 3] = ox [ 2];
assign ix [ 4] = ox [ 3];
assign ix [ 5] = ox [ 4];
assign ix [ 6] = ox [ 5];
assign ix [ 7] = ox [ 6];
assign ix [ 8] = ox [ 7];
assign ix [ 9] = ox [ 8];
assign ix [10] = ox [ 9];
assign ix [11] = ox [10];
assign ix [12] = ox [11];
assign ix [13] = ox [12];
assign ix [14] = ox [13];
assign ix [15] = ox [14];
assign iy [ 0] = 0;
assign iy [ 1] = oy [ 0];
assign iy [ 2] = oy [ 1];
assign iy [ 3] = oy [ 2];
assign iy [ 4] = oy [ 3];
assign iy [ 5] = oy [ 4];
assign iy [ 6] = oy [ 5];
assign iy [ 7] = oy [ 6];
assign iy [ 8] = oy [ 7];
assign iy [ 9] = oy [ 8];
assign iy [10] = oy [ 9];
assign iy [11] = oy [10];
assign iy [12] = oy [11];
assign iy [13] = oy [12];
assign iy [14] = oy [13];
assign iy [15] = oy [14];
assign y = oy [15];
endmodule

Правда как вы понимаете, у этой версии есть очень противная черта - многословие. К счастью, в районе 2000-го года в новый стандарт верилога (Verilog 2000 который из-за опоздания стал Verilog 2001) спионерили полезную конструкцию из VHDL под названием generic и с ее помощью адское многословие Verilog-95 удалось обуздать. До появления generate в верилоге наиболее хитрозадые пользователи использовали Perl-генерируемый код, при виде которого возникало желание никогда не связываться с этой профессией, а стать феминистическим журналистом, как Наталья Радулова.
Все еще комбинационная версия, использует generate и genvar:
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/006_combinational/isqrt.v
// combinational structured
module isqrt
(
input [31:0] x,
output [15:0] y
);
localparam [31:0] m = 32'h4000_0000;
wire [31:0] ix [0:15], iy [0:15];
wire [31:0] ox [0:15], oy [0:15];
generate
genvar i;
for (i = 0; i < 16; i = i + 1)
begin : u
isqrt_slice #(.m (m >> i * 2)) inst
(
.ix (ix [i]),
.iy (iy [i]),
.ox (ox [i]),
.oy (oy [i])
);
end
for (i = 1; i < 16; i = i + 1)
begin : v
assign ix [i] = ox [i - 1];
assign iy [i] = oy [i - 1];
end
endgenerate
assign ix [0] = x;
assign iy [0] = 0;
assign y = oy [15];
endmodule
Почти готово.
9. Конвейерная имплементация с 16 стадиями конвейера
После этой версии все, что нам нужно сделать, чтобы превратить комбинационный дизайн в конвейерный дизайн с 16-ю стадиями конвейера - это заменить комбинационный модуль isqrt_slice на его версию isqrt_slice_reg, в котором на выходах стоят регистры:
Переименовываем комбинационный модуль isqrt_slice, чтобы не перепутать:
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/007_pipelined_16_stages/isqrt_slice_comb.v
И вот версия с регистрами
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/007_pipelined_16_stages/isqrt_slice_reg.v
module isqrt_slice_reg
(
input clock,
input reset_n,
input [31:0] ix,
input [31:0] iy,
output reg [31:0] ox,
output reg [31:0] oy
);
parameter [31:0] m = 32'h4000_0000;
wire [31:0] cox, coy;
isqrt_slice_comb #(.m (m)) i
(
.ix ( ix ),
.iy ( iy ),
.ox ( cox ),
.oy ( coy )
);
always @(posedge clock or negedge reset_n)
begin
if (! reset_n)
begin
ox <= 0;
oy <= 0;
end
else
begin
ox <= cox;
oy <= coy;
end
end
endmodule
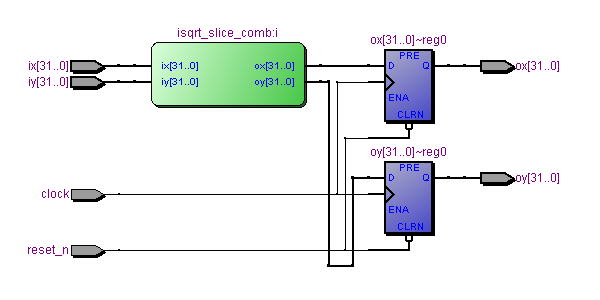
Конвейерная версия хардверной имплементации квадратного корня с 16-ю стадиями конвейера:
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/007_pipelined_16_stages/isqrt.v
// pipelined - 16 stages
module isqrt
(
input clock,
input reset_n,
input [31:0] x,
output [15:0] y
);
localparam [31:0] m = 32'h4000_0000;
wire [31:0] ix [0:15], iy [0:15];
wire [31:0] ox [0:15], oy [0:15];
generate
genvar i;
for (i = 0; i < 16; i = i + 1)
begin : u
isqrt_slice_reg #(.m (m >> i * 2)) inst
(
.clock ( clock ),
.reset_n ( reset_n ),
.ix ( ix [i] ),
.iy ( iy [i] ),
.ox ( ox [i] ),
.oy ( oy [i] )
);
end
for (i = 1; i < 16; i = i + 1)
begin : v
assign ix [i] = ox [i - 1];
assign iy [i] = oy [i - 1];
end
endgenerate
assign ix [0] = x;
assign iy [0] = 0;
assign y = oy [15];
endmodule
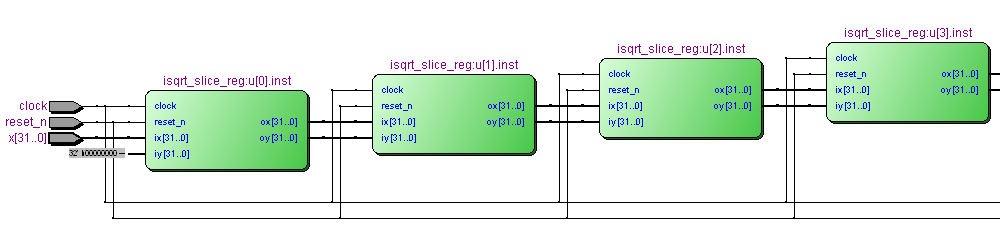
Пропускная способность (количество вычислений квадратного корня в секунду) у данного устройства будет 175 миллионов вычислений при имплементации на Altera Cyclone II. Хотя каждый отдельный корень будет проходить через устройство за 16 циклов или (1000 / 175) * 16 = примерно 90 наносекунд, одновременно в устройстве будут находится 16 корней на разных стадиях обработки, т.е. обрабатываться будет корень в цикл.
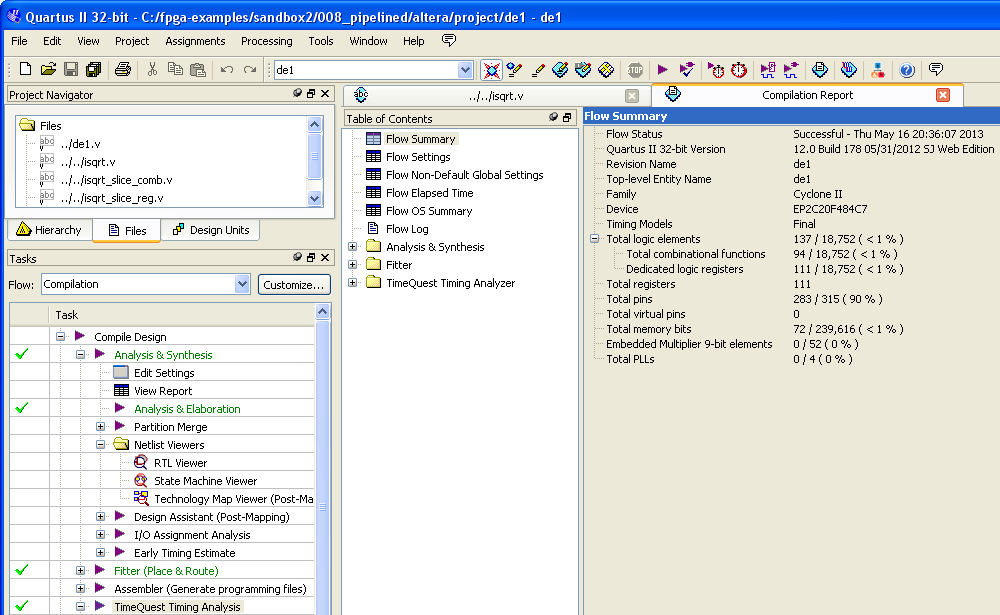
Также стоит учесть, что данный модуль займет менее одного процента ресурсов FPGA, т.е. мы можем насовать в один FPGA кучу таких модулей и вычислять миллиарды квадратных корней в секунду:
Timing report:
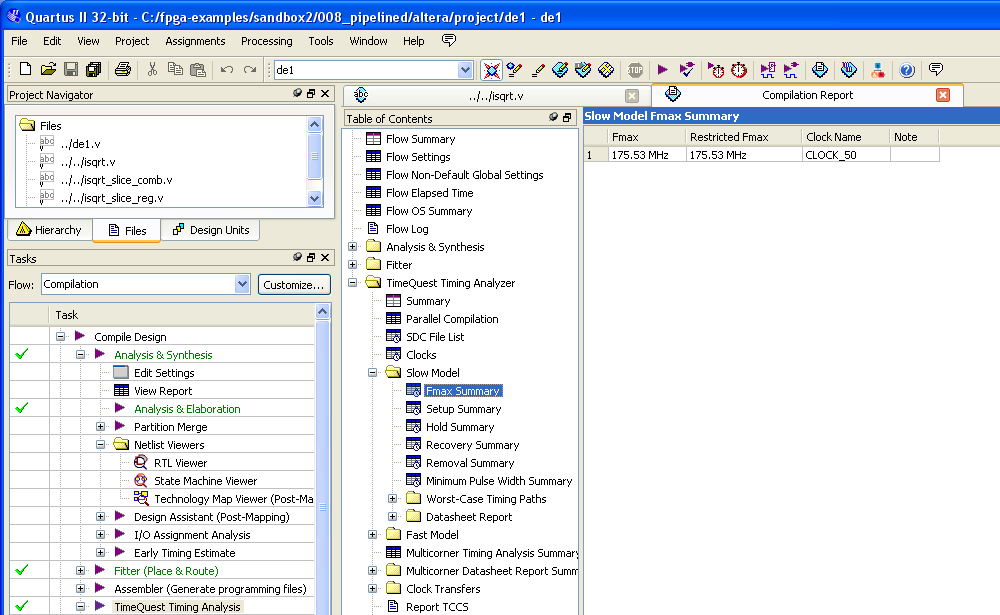
Fitter report:
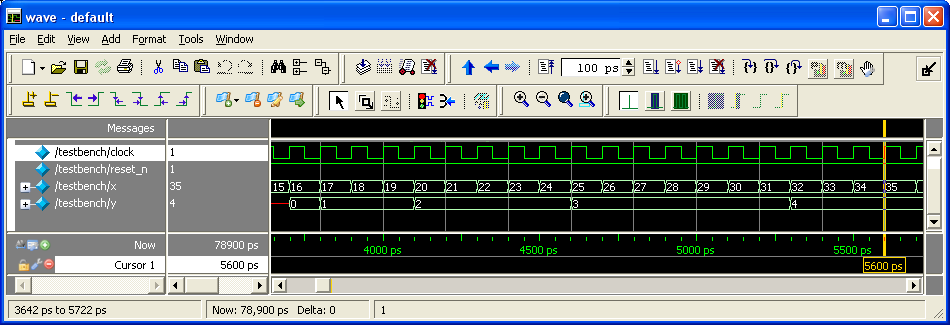
Для иллюстрации поведения дизайнов во времени по циклам тактового сигнала привожу три теста и три waveform diagrams, сделанные в бесплатной версии ModelSim-а. Правда имейте в виду, что я не ставил реальный timescale, т.е. все числа пикосекунд нужно игнорировать и ориентироваться только по тактовому сигналу. Комбинационный же дизайн симулируется как работающий мгновенно (т.е. все действия внутри вычислительного модуля происходят за время 0:
Тесты для комбинационной, секвенциальной и конвейерной имплементаций:
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/006_combinational/testbench.v
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/003_sequential/testbench.v
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/008_pipelined/testbench.v
Waveform diagrams для комбинационной, секвенциальной и конвейерной имплементаций:
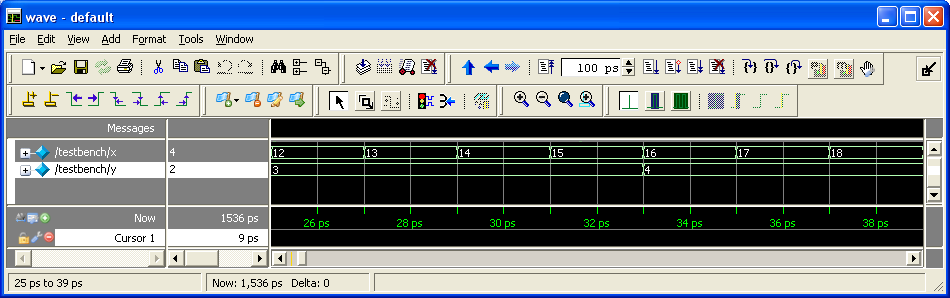
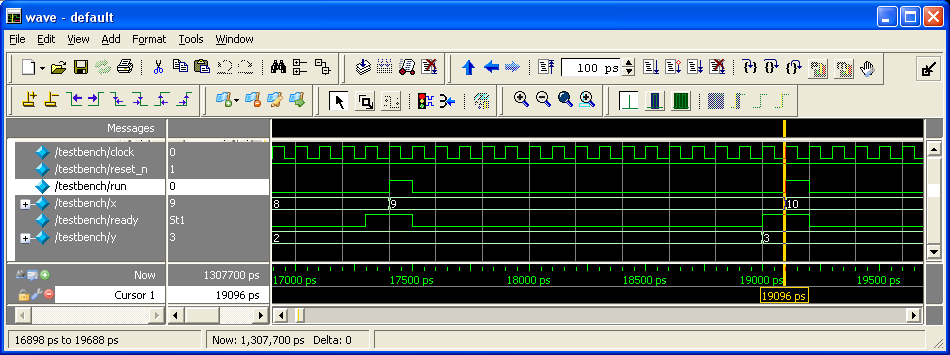
10. Конвейерная имплементация с параметризуемым количеством стадий конвейера - 1, 2, 4, 8 или 16 стадий
И наконец, с небольшим творческим усилием можно сделать модуль параметризуемым - с возможностью задания ему количества стадий конвейера - 1, 2, 4, 8 или 16 стадий.
http://fpga-examples.googlecode.com/svn/trunk/showroom/isqrt/008_pipelined/isqrt.v
// pipelined with configurable number of stages
module isqrt
(
input clock,
input reset_n,
input [31:0] x,
output [15:0] y
);
parameter n_pipe_stages = 16;
localparam n_slices = 16;
localparam n_slices_per_stage = n_slices / n_pipe_stages;
localparam [31:0] m = 32'h4000_0000;
wire [31:0] ix [0:15], iy [0:15];
wire [31:0] ox [0:15], oy [0:15];
generate
genvar i;
for (i = 0; i < 16; i = i + 1)
begin : u
if (i % n_slices_per_stage != n_slices_per_stage - 1)
begin
isqrt_slice_comb #(.m (m >> i * 2)) inst
(
.ix ( ix [i] ),
.iy ( iy [i] ),
.ox ( ox [i] ),
.oy ( oy [i] )
);
end
else
begin
isqrt_slice_reg #(.m (m >> i * 2)) inst
(
.clock ( clock ),
.reset_n ( reset_n ),
.ix ( ix [i] ),
.iy ( iy [i] ),
.ox ( ox [i] ),
.oy ( oy [i] )
);
end
end
for (i = 1; i < 16; i = i + 1)
begin : v
assign ix [i] = ox [i - 1];
assign iy [i] = oy [i - 1];
end
endgenerate
assign ix [0] = x;
assign iy [0] = 0;
assign y = oy [15];
endmodule
В зависимости от параметра синтезатор будет вставлять либо комбинационные модули, либо модули с регистрами:
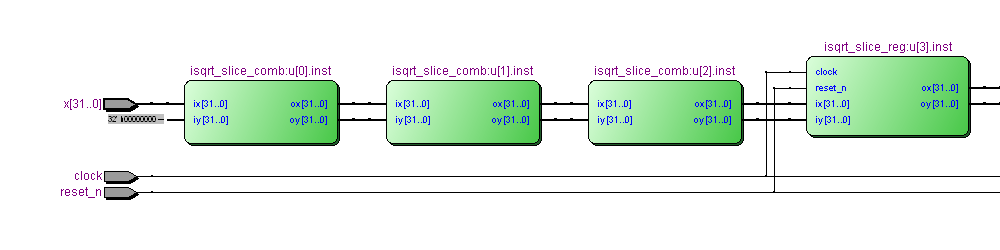
Версия с 4 стадиями конвейера (фрагмент):
Версия с 8 стадиями конвейера (фрагмент):
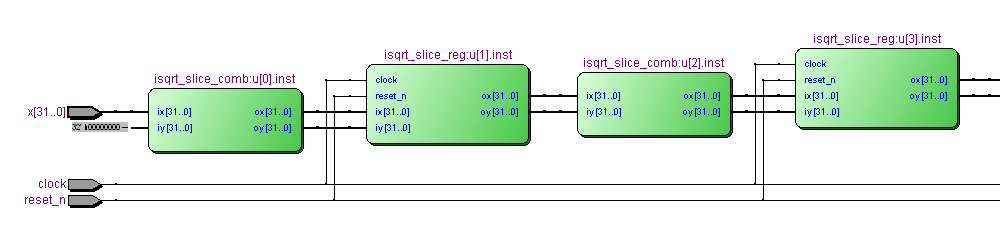
Соответственно будет изменяться количество логических функций, количество регистров и максимальная тактовая частота.
Я сделал табличку для синтеза на Altera Cyclone II, на нем все довольно нелинейно, но вы можете увидеть так сказать тренд в тактовой частоте:
# стадий конвейера
# комбинаторных функций
# регистров
частота, MHz
1
82
5
n/a
2
82
15
79.38
4
142
38
74.31
8
102
48
127.18
16
94
111
175.53
А вот пепелац, на котором я прогнал все тесты вживую с миганиями лампочек - студенческая плата Altera / Terasic DE1:
Poll Почему микроэлектроника не сводится к гонке за нанометрами