СИНГУЛЯРНОЕ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ
- уравнение, содержащее искомую функцию под знаком несобственного интеграла в смысле главного значения по Коши. В зависимости от размерности многообразия, по к-рому распространены интегралы, различают одномерные и многомерные С. и. у. По сравнению с теорией уравнений Фредгольма теория С. и. у. является более сложной.
[Spoiler (click to open)]
Так, напр., теории одномерных и многомерных С. и. у. как в смысле формулировок окончательных результатов, так и применяемых для их установления методов значительно отличаются друг от друга. Теория одномерных С. и. у. разработана более полно, причем ее результаты формулируются проще, чем аналогичные результаты в многомерном случае. Ниже в основном будет рассмотрен одномерный случай.
Важным классом одномерных С. и. у. являются уравнения с ядром Коши:
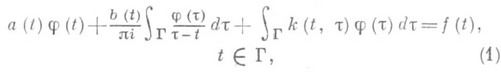
где а, b, k, f - известные функции, из к-рых k- ядро Фредгольма (см. Интегральный оператор),j - искомая функция, Г - плоская линия, а несобственный интеграл понимается в смысле главного значения по Коши, т. е.

где Г e=Гle , le обозначает дугу t'tt " линии Г такую, что длины дуг tt' и tt " равны e.
Оператор К, определяемый левой частью равенства (1), наз. сингулярным оператором (иногда его наз. общим сингулярным оператором):
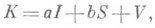
где I - тождественный оператор, S - сингулярный интегральный оператор (иногда его наз. сингулярным интегральным оператором с ядром Коши), т. е.

Оператор K0=aI+bS наз. характеристической частью сингулярного оператора К, или характеристическим сингулярным оператором, а уравнение
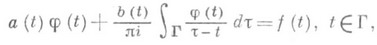
- характеристическим С. и. у., функции а, b - коэффициентами соответствующего оператора или уравнения.
Уравнение

наз. союзнымс уравнением (1), а оператор K'=aI+SbI+V'(V'- интегральный оператор с ядром k(t, t)) - союзным с оператором К. В частности, К'0=аI+SbI является союзным с К 0.
Операторы К, К 0, К', К'0 или соответствующие им уравнения наз. нормального типа, если функции
А=а+b, В=а-b
не обращаются в нуль нигде на Г. В этом случае говорят также, что коэффициенты оператора или уравнения удовлетворяют условию нормальности.
Большое теоретическое и прикладное значение С. и. у. особенно проявилось с кон. 30-х гг. в связи с решением нек-рых весьма важных задач механики сплошной среды (теории упругости, гидро- и аэромеханики и др.) и теоретич. физики. Теория одномерных С. и. у. была значительно продвинута в 40-х гг. и получила в определенном смысле законченный вид в трудах советских математиков. Изложение такой теории одномерных С. и. у. в гёльдеровых классах функций дано в монографии одного из создателей этой теории Н. И. Мусхелишвили (см. [1]). Эта монография стимулировала научные исследования и в нек-рых других направлениях, напр. в теории С. и. у., не удовлетворяющих условию нормальности по Хаусдорфу, С. и. у. с недиагональными особенностями (со смещениями), уравнений Винера - Хопфа, многомерных С. и. у. и т. д. Первые исследования по многомерным С. и. у. принадлежат Ф. Трикоми (F. Tricomi, 1928), к-рый установил формулу перестановки двумерных сингулярных интегралов и применил ее к решению одного класса С. и. у. В этом направлении фундаментальное исследование принадлежит Ж. Жиро (G. Giraud, 1934), доказавшему справедливость теорем Фредгольма для нек-рых классов многомерных С. и. у. на ляпуновских многообразиях.
Лит.:[1] Мусхелишвили Н. И., Сингулярные интегральные уравнения, 3 изд., М., 1968; [2] Гахов Ф. Д., Краевые задачи, 3 изд., М., 1977; [3] Векуа Н. П., Системы сингулярных интегральных уравнений и некоторые граничные задачи, 2 изд., М., 1970; [4] Хведелидзе Б. В., "Тр. Тбилисск. матем. ин-та АН Груз. ССР", 1956, т. 23, с. 3-158; [5] Данилюк И. И., Нерегулярные граничные задачи на плоскости, М., 1975; [6] Гохберг И. Ц., Крупник Н., Введение в теорию одномерных сингулярных интегральных операторов, Киш., 1973; [7] Михлин С. Г., Многомерные сингулярные интегралы и интегральные уравнения, М., 1962; [8] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966: [9] Nоеthеr F., "Math. Ann.", 1921, Bd 82, S. 42-63; [10] Саrlemаn Т., "Arkiv mat., astron. och fys.", 1922, Bd 16, № 26, S. 1-19; [1l] Пресдорф 3., Некоторые классы сингулярных уравнений, пер. с нем., М , 1979 А. В. Бицадзе, Б. В. Хведелидзе.
[Spoiler (click to open)]
Так, напр., теории одномерных и многомерных С. и. у. как в смысле формулировок окончательных результатов, так и применяемых для их установления методов значительно отличаются друг от друга. Теория одномерных С. и. у. разработана более полно, причем ее результаты формулируются проще, чем аналогичные результаты в многомерном случае. Ниже в основном будет рассмотрен одномерный случай.
Важным классом одномерных С. и. у. являются уравнения с ядром Коши:
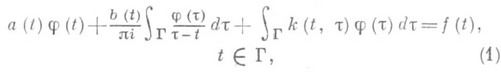
где а, b, k, f - известные функции, из к-рых k- ядро Фредгольма (см. Интегральный оператор),j - искомая функция, Г - плоская линия, а несобственный интеграл понимается в смысле главного значения по Коши, т. е.

где Г e=Гle , le обозначает дугу t'tt " линии Г такую, что длины дуг tt' и tt " равны e.
Оператор К, определяемый левой частью равенства (1), наз. сингулярным оператором (иногда его наз. общим сингулярным оператором):
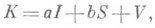
где I - тождественный оператор, S - сингулярный интегральный оператор (иногда его наз. сингулярным интегральным оператором с ядром Коши), т. е.

Оператор K0=aI+bS наз. характеристической частью сингулярного оператора К, или характеристическим сингулярным оператором, а уравнение
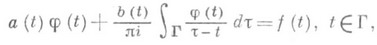
- характеристическим С. и. у., функции а, b - коэффициентами соответствующего оператора или уравнения.
Уравнение

наз. союзнымс уравнением (1), а оператор K'=aI+SbI+V'(V'- интегральный оператор с ядром k(t, t)) - союзным с оператором К. В частности, К'0=аI+SbI является союзным с К 0.
Операторы К, К 0, К', К'0 или соответствующие им уравнения наз. нормального типа, если функции
А=а+b, В=а-b
не обращаются в нуль нигде на Г. В этом случае говорят также, что коэффициенты оператора или уравнения удовлетворяют условию нормальности.
Большое теоретическое и прикладное значение С. и. у. особенно проявилось с кон. 30-х гг. в связи с решением нек-рых весьма важных задач механики сплошной среды (теории упругости, гидро- и аэромеханики и др.) и теоретич. физики. Теория одномерных С. и. у. была значительно продвинута в 40-х гг. и получила в определенном смысле законченный вид в трудах советских математиков. Изложение такой теории одномерных С. и. у. в гёльдеровых классах функций дано в монографии одного из создателей этой теории Н. И. Мусхелишвили (см. [1]). Эта монография стимулировала научные исследования и в нек-рых других направлениях, напр. в теории С. и. у., не удовлетворяющих условию нормальности по Хаусдорфу, С. и. у. с недиагональными особенностями (со смещениями), уравнений Винера - Хопфа, многомерных С. и. у. и т. д. Первые исследования по многомерным С. и. у. принадлежат Ф. Трикоми (F. Tricomi, 1928), к-рый установил формулу перестановки двумерных сингулярных интегралов и применил ее к решению одного класса С. и. у. В этом направлении фундаментальное исследование принадлежит Ж. Жиро (G. Giraud, 1934), доказавшему справедливость теорем Фредгольма для нек-рых классов многомерных С. и. у. на ляпуновских многообразиях.
Лит.:[1] Мусхелишвили Н. И., Сингулярные интегральные уравнения, 3 изд., М., 1968; [2] Гахов Ф. Д., Краевые задачи, 3 изд., М., 1977; [3] Векуа Н. П., Системы сингулярных интегральных уравнений и некоторые граничные задачи, 2 изд., М., 1970; [4] Хведелидзе Б. В., "Тр. Тбилисск. матем. ин-та АН Груз. ССР", 1956, т. 23, с. 3-158; [5] Данилюк И. И., Нерегулярные граничные задачи на плоскости, М., 1975; [6] Гохберг И. Ц., Крупник Н., Введение в теорию одномерных сингулярных интегральных операторов, Киш., 1973; [7] Михлин С. Г., Многомерные сингулярные интегралы и интегральные уравнения, М., 1962; [8] Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966: [9] Nоеthеr F., "Math. Ann.", 1921, Bd 82, S. 42-63; [10] Саrlemаn Т., "Arkiv mat., astron. och fys.", 1922, Bd 16, № 26, S. 1-19; [1l] Пресдорф 3., Некоторые классы сингулярных уравнений, пер. с нем., М , 1979 А. В. Бицадзе, Б. В. Хведелидзе.