Sequences and differences
While I was in Portland, vruba introduced me to a curiosity: Take the sequence x2:
1, 4, 9, 16, 25, ... (i.e. 1 squared, 2 squared, 3 squared, ...)
Now, subtract each number from the next one:
4 - 1 = 3
9 - 4 = 5
16 - 9 = 7
...
to get this sequence:
3, 5, 7, 9, ...
Repeat this, and you end up with:
2, 2, 2, 2, ...
Put together in a table, this looks like:
1491625...
3579...
222...
Now, vruba pointed out that by assuming the bottom row is always going to consist of 2s (which it looks like it will), we can then calculate the next number in the original sequence. The 2s in the bottom row tell us that the difference between the numbers in the middle row is always 2... so the next number in the middle row should be 9 + 2, or 11:
1491625...
357911...
2222...
But then that tells us that the difference between 25 and the next number in the first row is 11... so the next number in the first row shoule be 25 + 11, or 36:
149162536...
357911...
2222...
And indeed, 36 is 6 squared, the next number in the sequence. Now, this way of figuring out the sequence might seem a little convoluted, but consider this. You might immediately recognize the first row as being squares of numbers, but a computer wouldn't. But, if you gave a computer the first row, and it used this method, it could figure out the rest of the sequence without knowing anything about the sequence other than the few numbers you gave it.
I decided to play around with this technique some more, and found some very interesting things.
First, it works for more than x2. Here's x3:
182764125216...
719376191...
12182430...
666...
Again, we could figure out what the next number in the first row is by working up from the bottom row (this is called "extrapolation").
I started trying this for other things, such as x4 and x5, and noticed two patterns.
The number of rows needed before the numbers become the same ("constant") seems to the be the power of x plus 1. So for x2 it takes three rows. For x3 it takes four rows. And so on.
Also, the constant number that you end up with appears to be the factorial of the power. (The best way to explain a factorial is by example. 5 factorial, written 5!, means 5*4*3*2*1. 6! = 6*5*4*3*2*1. It's just multiplication.) If you have x3, you end up with 3*2*1, or 6. If you have x5 you get 5!, which is 120.
Curious, no?
So I started looking for the underlying pattern. I tried looking at three consecutive, arbitrary numbers -- x, (x+1), and (x+2) -- and the sequence x2. Then I looked at x3, where it gets more interesting:
x3(x+1)3(x+2)3(x+3)3...
I expanded these out and subtracted:
(x+1)3 - x3 = (x3 + 3x2 + 3x + 1) - x3 = 3x2 + 3x + 1
and obtained:
x3(x+1)3(x+2)3(x+3)3...
3x2 + 3x + 13x2 + 9x + 73x2 + 15x + 19...
6x + 66x + 12...
6...
See how the power goes down by one in each row, and how the coefficient on the first term (starting in the second row) is 3, then 3*2, then 3*2*1? At this point, I started wondering if it has anything to do with differentiation, since you see a similar pattern there. But I couldn't figure out how this would have anything to do with calculus. We pulled out a calculus textbook and I was going to play around with it, but I got sidetracked explaining limits and differentiation to Rebecca.
I wrote a little perl script to create these sort of tables for me, and by playing around found out that this behaviour happens for any polynomial, and that it's only the highest power that affects what the final constant will be. (Note that if there's a coefficient on the highest-power term, it carries through and the eventual constant is multiplied by the coefficient.)
I played around some more, and tried to research it on the net, but didn't turn up anything until today.
Turns out that this sort of method is called a Finite Difference and it is the discrete analogue of differentiation.
(Discrete means talking about something at specific points. e.g. the sequence of x2 I was using above is what you get when you take x=1, x=2, x=3, ... and square them. If you plot x2 on a graph discretely (x on the horizontal, x2 on the vertical) you get:
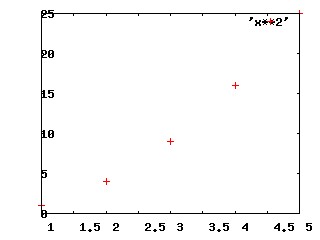
Whereas if you treat x2 continously, and you draw the graph, you get:
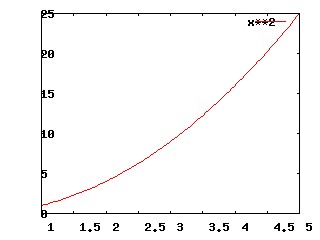
See how it's all points, not just certain points?)
Well, finite differences are what you do on discrete functions, whereas differentiation is what you do on continuous functions. So I was right, there is a connection.
I found several other useful pages:
Figuring out functions using finite differences
Another explanation
None of those directly explain why you get the factorial of the highest power, but I think it could be explained fairly easily (let me know if you figure it out). I haven't tried playing with it as a difference of polynomials in general form (akxk + ak-1xk-1 + ... + a2x2 + a1x + a0 where aj is the coefficient of the jth term) yet; I suspect this would yield the result. Similar to proving the power rule in calculus. Actually, I'm sure that it could be shown that addition isn't affected across finite differences, so you could look at the polynomial term by term, and prove that akxk becomes k*akxk-1.
Sorry, that got a bit technical at the end... ask me if you want a simpler breakdown or explanation of anything in here.
1, 4, 9, 16, 25, ... (i.e. 1 squared, 2 squared, 3 squared, ...)
Now, subtract each number from the next one:
4 - 1 = 3
9 - 4 = 5
16 - 9 = 7
...
to get this sequence:
3, 5, 7, 9, ...
Repeat this, and you end up with:
2, 2, 2, 2, ...
Put together in a table, this looks like:
1491625...
3579...
222...
Now, vruba pointed out that by assuming the bottom row is always going to consist of 2s (which it looks like it will), we can then calculate the next number in the original sequence. The 2s in the bottom row tell us that the difference between the numbers in the middle row is always 2... so the next number in the middle row should be 9 + 2, or 11:
1491625...
357911...
2222...
But then that tells us that the difference between 25 and the next number in the first row is 11... so the next number in the first row shoule be 25 + 11, or 36:
149162536...
357911...
2222...
And indeed, 36 is 6 squared, the next number in the sequence. Now, this way of figuring out the sequence might seem a little convoluted, but consider this. You might immediately recognize the first row as being squares of numbers, but a computer wouldn't. But, if you gave a computer the first row, and it used this method, it could figure out the rest of the sequence without knowing anything about the sequence other than the few numbers you gave it.
I decided to play around with this technique some more, and found some very interesting things.
First, it works for more than x2. Here's x3:
182764125216...
719376191...
12182430...
666...
Again, we could figure out what the next number in the first row is by working up from the bottom row (this is called "extrapolation").
I started trying this for other things, such as x4 and x5, and noticed two patterns.
The number of rows needed before the numbers become the same ("constant") seems to the be the power of x plus 1. So for x2 it takes three rows. For x3 it takes four rows. And so on.
Also, the constant number that you end up with appears to be the factorial of the power. (The best way to explain a factorial is by example. 5 factorial, written 5!, means 5*4*3*2*1. 6! = 6*5*4*3*2*1. It's just multiplication.) If you have x3, you end up with 3*2*1, or 6. If you have x5 you get 5!, which is 120.
Curious, no?
So I started looking for the underlying pattern. I tried looking at three consecutive, arbitrary numbers -- x, (x+1), and (x+2) -- and the sequence x2. Then I looked at x3, where it gets more interesting:
x3(x+1)3(x+2)3(x+3)3...
I expanded these out and subtracted:
(x+1)3 - x3 = (x3 + 3x2 + 3x + 1) - x3 = 3x2 + 3x + 1
and obtained:
x3(x+1)3(x+2)3(x+3)3...
3x2 + 3x + 13x2 + 9x + 73x2 + 15x + 19...
6x + 66x + 12...
6...
See how the power goes down by one in each row, and how the coefficient on the first term (starting in the second row) is 3, then 3*2, then 3*2*1? At this point, I started wondering if it has anything to do with differentiation, since you see a similar pattern there. But I couldn't figure out how this would have anything to do with calculus. We pulled out a calculus textbook and I was going to play around with it, but I got sidetracked explaining limits and differentiation to Rebecca.
I wrote a little perl script to create these sort of tables for me, and by playing around found out that this behaviour happens for any polynomial, and that it's only the highest power that affects what the final constant will be. (Note that if there's a coefficient on the highest-power term, it carries through and the eventual constant is multiplied by the coefficient.)
I played around some more, and tried to research it on the net, but didn't turn up anything until today.
Turns out that this sort of method is called a Finite Difference and it is the discrete analogue of differentiation.
(Discrete means talking about something at specific points. e.g. the sequence of x2 I was using above is what you get when you take x=1, x=2, x=3, ... and square them. If you plot x2 on a graph discretely (x on the horizontal, x2 on the vertical) you get:

Whereas if you treat x2 continously, and you draw the graph, you get:

See how it's all points, not just certain points?)
Well, finite differences are what you do on discrete functions, whereas differentiation is what you do on continuous functions. So I was right, there is a connection.
I found several other useful pages:
Figuring out functions using finite differences
Another explanation
None of those directly explain why you get the factorial of the highest power, but I think it could be explained fairly easily (let me know if you figure it out). I haven't tried playing with it as a difference of polynomials in general form (akxk + ak-1xk-1 + ... + a2x2 + a1x + a0 where aj is the coefficient of the jth term) yet; I suspect this would yield the result. Similar to proving the power rule in calculus. Actually, I'm sure that it could be shown that addition isn't affected across finite differences, so you could look at the polynomial term by term, and prove that akxk becomes k*akxk-1.
Sorry, that got a bit technical at the end... ask me if you want a simpler breakdown or explanation of anything in here.